Примеры в несколько действий
| 3+12:2 | 96+18:9-76 |
| 55-2×3 | 5×9-24:4 |
| 9×(5-3) | 7×5+(80-55) |
| (41+3):4 | 85+3×(6-2) |
| 9×(8-5):3 | (64+4×8):2 |
| 4+40:8 | 74+24:3-75 |
| 48-5×9 | 3×4-54:9 |
| 4×(4-2) | 7×6+(32-13) |
| (86+5):7 | 74+2×(7-5) |
| 5×(6-4):2 | (60+4×3):6 |
| 5+12:2 | 60+39:3-61 |
| 22-4×5 | 6×2-28:4 |
| 6×(8-2) | 9×4+(71-17) |
| (54+9):9 | 24+6×(5-2) |
| 2+20:4 | 5×(9-7):2 |
| 65-4×4 | (51+9×3):6 |
| 9×(9-2) | 70+72:9-75 |
| (21+9):3 | 9×8+(45-22) |
| 9×2-44:4 | 50+4×(8-5) |
| 5×(7-4):3 | (74+2×5):3 |
| 5+48:8 | 56+72:2-23 |
| 95-6×2 | 9×8-28:2 |
| 3×(8-3) | 4×9+(47-12) |
| (73+5):6 | 76+6×(9-5) |
| 4×(7-2):5 | (36+4×7):2 |
| 8+80:5 | 78+88:4-21 |
| 82-4×2 | 2×7+(70-30) |
| 4×(5-2) | 75+2×(8-6) |
| (36+9):5 | 6×(9-4):5 |
| 9×5-96:6 | (24+6×7):3 |
Карточка 1.
42: 6 + (19 + 6): 5 – 6 • 2
(27 – 19) • 4 + 18: 3 + (8 + 27): 5 – 17
60 – (13 + 22): 5 – 6 • 4 + 25
Карточка 2.
(82 – 74): 2 • 7 + 7 • 4 – 19 + (63 – 27): 4
(91 – 83) • 3: 4 + 12: 6
32: 8 + (27 + 15): 6 + 8 • 5
Карточка 3.
9 • 5 – 36: 6: 2 – (38 – 23): 5
90 – (40 – 24: 3): 4 • 6 + 3 • 5
3 • 4 + 9 • 6 – (27 + 9): 4 • 5
Карточка 4.
(50 – 23): 3 + 8 • 5 – 6 • 5 – (26 – 16) • 6
(5 • 6 – 3 • 4 + 48: 6) + (82 – 78) • 7 – 13
(69 – 45): 3 • 2 + (43 – 34) • 2
Карточка 5.
9 • 6 – 6 • 4: (33 – 25) • 7
(5 • 9 – 25): 4 • 8 – 4 • 7 – 13
3 • (12 – 8): 2 + 6 • 9 - 33
Карточка 6.
(76 – (27 + 9) + 8): 6 • 4
9 • (2 • 3) – 48: 8 • 3 + 7 • 6 – 34
(7 • 4 + 33) – 3 • 6: 2
Карточка 7.
(9 • 4 – 6 • 5) • 4 – 42: 7 + (60 – 11)
7 • 6 + 9 • 4 – (2 • 7 + 54: 6 • 5)
(37 + 7 • 4 – 17): 6 + 7 • 5
33 + 9 • 3 – (85 – 67): 2 • 6
Карточка 8.
28: 4 + 27: 3 – (17 + 31): 6
54: 9 + (8 + 19): 3 – 32:4
(8 • 6 – 36: 6): 6 • 3 + 5 • 9
21: 7 + (42 – 14): 4 – (44 – 14): 5
Карточка 9.
8 • 5 – (60 – 42): 3 + 9 • 2
5 • 7 + (18 +14): 4 – (26 – 8): 3 • 2
(58 – 31): 3 – 2 + (58 – 16): 6
1. Реши примеры.
1.1) 35: 5 + (23 + 7): 5 – 3 * 4 =
1.2) (39 – 19) * 3 + 24: 3 + (9 + 36): 5 – 13 =
1.3) 760 – (14 + 31): 5 – 6 * 3 + 41 =
1.4) (52 – 34): 2 * 8 + 7 * 3 – 13 + (64 – 44): 4 =
1.5) (87 – 79) * 9: 3 + 9 * 6 =
1.6) 45: 9 + (13 + 22): 5 + 4 * 6 =
1.7) 8 * 5 – 14: 7: 2 – (42 – 24): 6=
1.8) 70 – (15 + 24: 3) + 4 * 3 + 8 * 2=
1.9) 5 * 3 + 7 * 4 – (1 + 9): 2 * 6 =
2. Расставь правильно скобки.
2.1) 3 + 6: 3 + 3 * 3 = 6
2.2) 3 + 6: 3 + 3 * 3 = 14
2.3) 3 + 6: 3 + 3 * 3 = 12
2.4) 3 + 6: 3 + 3 * 3 = 18
3. Расставь скобки различными способами и реши получившиеся примеры.
3.1) 5 + 5 - 5 * 5 + 5 =
3.2) 5 + 5 - 5 * 5 + 5 =
3.3) 5 + 5 - 5 * 5 + 5 =
3.4) 5 + 5 - 5 * 5 + 5 =
3.5) 6 * 6 - 6 + 6: 6 =
3.6) 6 * 6 - 6 + 6: 6 =
3.7) 6 * 6 - 6 + 6: 6 =
3.8) 6 * 6 - 6 + 6: 6 =
3.9) 7 - 7 * 7 + 7: 7 =
3.10) 7 - 7 * 7 + 7: 7 =
3.11) 7 - 7 * 7 + 7: 7 =
3.12) 7 - 7 * 7 + 7: 7 =
4. Расставь скобки разными способами и реши получившиеся примеры.
4.1) 12: 4 + 56: 7 - 36: 6 + 13 =
a) __________
б) __________
в) __________
г) __________
4.2) 32 + 18: 3 + 14 * 3 + 81: 9 =
a) __________
б) __________
в) __________
г) __________
4.3) 56: 8 + 8 * 5 - 72: 8 =
a) __________
б) __________
в) __________
г) __________
Законы арифметики
Переместительный закон сложения
Запомните! 
От перемены мест слагаемых сумма не меняется.
(Значение суммы при перестановке слагаемых не меняется.)

Примеры:
· 90 + 20 = 20 + 90 = 110
Сочетательный закон сложения
Запомните! 
Значение суммы не зависит от того, как сгруппированы слагаемые.
(Порядок выполнения действий при вычислении суммы не влияет на конечный результат.)

Например:
· 6 + 4 + (3 + 2) = 6 + (4 + 3) + 2 = (6 + 4) + 3 + 2 = 15
Обратите внимание, этот закон действует только, если все действия в примере сложение!
Переместительный закон умножения
Запомните! 
От перемены мест множителей произведение не меняется.
(Значение произведения при перестановке множителей не меняется.)

Сочетательный закон умножения
Запомните! 
Значение произведения не зависит от того, как сгруппированы множители.
(Порядок выполнения действий при расчёте произведения не влияет на конечный результат.)

Распределительный закон умножения относительно сложения
Запомните! 
Чтобы сумму умножить на число, можно умножить на это число каждое из слагаемых, а затем сложить полученные произведения.

Источник: http://math-prosto.ru
Запомните! 
Периметр — это сумма длин всех сторон многоугольника.
Иногда для вычисления периметра геометрических фигур используются специальные формулы, в которых периметр обозначается заглавной латинской буквой P.
Периметр измеряется в единицах длины: мм, см, м, км и т.д.
Запомните! 
Периметр прямоугольника — это сумма длины и ширины, умноженная на 2.
P = (a + b) · 2, где a — длина прямоугольника, b — ширина прямоугольника.
Стороны прямоугольника, которые лежат друг против друга (противолежащие), мы называем длиной и шириной.
 AB = 3 см, BC = 7 см
AB = 3 см, BC = 7 см
PABCD= (AB + BC) · 2
PABCD= (7 + 3) · 2 = 10 · 2 = 20 (см)
Запомните! 
Периметр квадрата — это длина стороны квадрата, умноженная на 4.
P = a · 4, где a — длина стороны квадрата.
 KE = 7 см
KE = 7 см
PEKFM= 4 · KE
PEKFM= 4 · 7 = 28 (см)
Как найти периметр многоугольника
Периметр любого многоугольника (в том числе и периметр треугольника) рассчитывается по определению периметра. Для этого надо просто сложить длины всех сторон многоугольника.

PABCDE= AB + BC + CD + DE + EA = 3 + 4 + 3 + 2 + 2 = 14 (см)
Порядок действий
Если в выражении скобок нет, то:
· сначала выполняем слева направо все действия умножения и деления;
· а потом слева направо все действия сложения и вычитания
·Рассмотрим порядок действий в следующем примере.
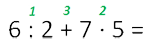
Напоминаем вам, что порядок действий в математике расставляется слева направо (от начала к концу примера).
При вычислении значения выражения можно вести запись двумя способами.
Первый способ
· Каждое действие записывается отдельно со своим номером под примером.
· После выполнения последнего действия ответ обязательно записывается в исходный пример.

Запомните! 
При расчёте результатов действий с двузначными и/или трёхзначными числами обязательно приводите свои расчёты в столбик.

Второй способ
· Второй способ называется запись "цепочкой". Все вычисления проводятся в точно таком же порядке действий, но результаты записываются сразу после знака равно.

Запомните! 
Если выражение содержит скобки, то сначала выполняют действия в скобках.
Внутри самих скобок действует правило порядка действий как в выражениях без скобок.

Если внутри скобок находятся ещё одни скобки, то сначала выполняются действия внутри вложенных (внутренних) скобок.







