Begin- Return iterator to beginning
End- Return iterator to end| for (it=m1.begin(); it!= m1.end(); it++) { cout << it->first << ": " << it->second << endl; } EraseRemoves from the map container either a single element or a range of elements map<string,string>::iterator it; it=mymap.find('b'); mymap.erase (it); // erasing by iterator mymap.erase ('c'); // erasing by key Find Searches the container for an element with a key equivalent to k and returns an iterator to it if found, otherwise it returns an iterator to map::end. cout << "a => " << mymap.find('a')->second << '\n'; |
Clear
Removes all elements from the map container (which are destroyed), leaving the container with a size of 0.
std::map<char, int> mymap;
mymap['x'] = 100;
mymap.clear();
a. Priority Queue
v. Definition:
The STL priority_queue adapter provides to programmers an interface suitable for as a priority queue. Priority queues, however, allow access to only the item with the highest priority.
vi. C++ realization:
priority_queue<int> pq;vii. Conditional ordering
viii. Inserting and removing functions.
priority_queue<int> mypq; mypq.push(30); mypq.pop();1. Graphs
a. Definition
b. Vertex, edge:
A graph G = (V,E) is composed of:
V: set of vertices
E: set of edges connecting the vertices in V
An edge e = (u,v) is a pair of vertices
c. Graphs applications: communication,circuits, mechanical, hydraulic, transportation, software systems,internet, games, social relationship and etc.
d. Undirected, Directed graphs:
A directed graph consists of a set V of vertices or nodes and a set E of edges or arcs. Each edge has a source node and a target node, and the edge can be traversed only from source to target.
In undirected graphs each edge can be traversed in either direction.
e. Complete graphs - a simple graph in which each pair of distinct vertices are adjacent is a complete graph.
f. Adjacent vertices, neighbours:
Two vertices in a graph are adjacent if they form an edge. For example, Anchorage and Corvallis are adjacent, while Anchorage and Denver are not. Adjacent vertices are called neighbours.
g. Isolated vertex
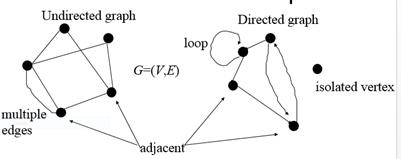
h. Degree of a Vertex: degree of a vertex: number of edges connected

i. Path, trail, walk
path: no vertex can be repeated
a-b-c-d-e
trail: no edge can be repeat
a-b-c-d-e-b-d
walk: no restriction
a-b-d-a-b-c
j. Closed (path, trail, walk)
2. closed if x = y
3. closed trail: circuit (a-b-c-d-b-e-d-a,
one draw without lifting pen)
5. closed path: cycle (a-b-c-d-a)
a. Length of a (path, trail, walk)
length: number of edges in
this (path,trail,walk)
b. Connected/not connected undirected/directed graphs
An undirected graph is connected if, for any pair of vertices, there is a path between them.
A directed graph is connected if, for any pair of vertices, there is a path between them.
C. Isomorphic graphs
 | |||
 |
d. Null graphs: a graph whose edge-set is empty is a null graph.

e. Cycle, path, wheel graphs 
f. Regular graphs 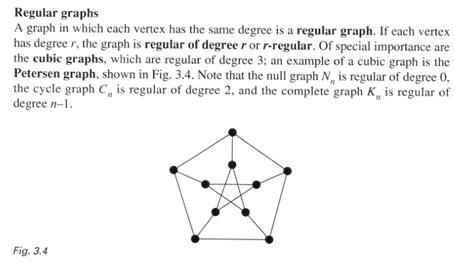
g. Platonic graphs