Определить:
1) фазные токи;
2) ток в нулевом проводе;
3) активную, реактивную и полную мощность каждой фазы и всей трехфазной цепи;
4) угол сдвига фаз между током и напряжением в каждой фазе;
5) начертить в масштабе векторную диаграмму трехфазной цепи;
6) результаты расчетов занести в соответствующие таблицы.


Рис.3.1
В цепи, изображенной на схеме (рис. 3.1), потребители трехфазного тока соединены звездой.
Известно линейное напряжение 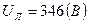 и сопротивления фаз:
и сопротивления фаз:
RA =15,36(Ом); RB =25,8(Ом); RC =12,5(Ом); XLA =12,9(Ом); XLC =21,65(Ом); XCB =30,7(Ом).
Определить полные сопротивления фаз, фазные токи и ток в нейтральном проводе, активную, реактивную и полную мощности каждой фазы и всей цепи. Построить векторную диаграмму цепи.
Дано: 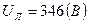 ; RA =15,36(Ом); RB =25,8(Ом); RC =12,5(Ом); XLA =12,9(Ом); XLC =21,65(Ом); XCB =30,7(Ом).
; RA =15,36(Ом); RB =25,8(Ом); RC =12,5(Ом); XLA =12,9(Ом); XLC =21,65(Ом); XCB =30,7(Ом).
Определить: ZA; ZB; ZC; IA; IB; IC; IN; PA; PB; PC; P; QA; QB; QC; Q; SA; SB; SC; S.
1. При соединении звездой  ,поэтому
,поэтому

Так как есть нейтральный провод, то UA= UB= UC= 199,76 (B).
Выразим в комплексной форме фазные напряжения:



2. Выразим комплексные сопротивления фаз в показательной форме:

где  - полное сопротивление фазы A;
- полное сопротивление фазы A;
 - угол сдвига фаз между током и напряжением в фазе А.
- угол сдвига фаз между током и напряжением в фазе А.
Аналогично определяем:

где  ,
,  .
.

где  ,
,  .
.
3. Находим комплексы фазных токов:

модуль  , аргумент
, аргумент  ;
;
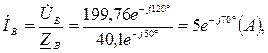
модуль  , аргумент
, аргумент  ;
;


модуль  , аргумент
, аргумент  .
.
Находим алгебраическую форму записи комплексов фазных токов:



4. Вычисляем ток в нейтральном проводе:


модуль  , аргумент
, аргумент 
5. Вычисляем мощности каждой фазы и всей цепи:
 ,
,
где 
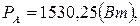

 ,
,
где 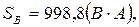
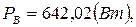

 ,
,
где 

тогда:


где 

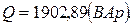
6. Строим в масштабе векторную диаграмму цепи.
На векторной диаграмме под углом 120° друг относительно друга строятся векторы фазных напряжений одинаковой длины.
Векторы фазных токов строятся в масштабе под вычисленными углами φ по отношению к фазным напряжениям. В фазе А нагрузка носит индуктивный характер, значит, ток  отстает от напряжения
отстает от напряжения  на угол
на угол  .
.
В фазе В нагрузка носит емкостный характер, следовательно, ток  опережает напряжение
опережает напряжение  нa угол
нa угол  .
.
В фазе С нагрузка индуктивная, следовательно, ток  отстает от напряжения
отстает от напряжения  на угол
на угол  .
.
 МI= 2,5(А/см) - масштаб.
МI= 2,5(А/см) - масштаб.






рис.3.2
7. Результаты расчетов занесем в соответствующие таблицы
Результаты расчета токов
| Фазные токи | Алгебраическая форма, А | Показательная форма, А | Действующее значение, А |

| 
| 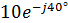
| |

| 
| 
| |

| 
| 
| |

| 
| 
|
Заключение
В первой части курсовой работы был проведен анализ линейной электрической цепи постоянного тока. В ней были определены токи во всех ветвях цепи двумя методами: метод контурных токов и метод наложения. Тем самым была выполнена и проверка результатов. Погрешность не превысила 5%. Был составлен баланс мощностей, погрешность расчета была менее 5%. Был определен ток во второй ветви методом эквивалентного генератора и построена потенциальная диаграмма замкнутого контура, включающего обе ЭДС.
Во второй части были определены действующие значения токов во всех ветвях, записано уравнение мгновенного значения тока источника. Был составлен баланс активных и реактивных мощностей, погрешность не превысила 5 %. Также была построена векторная диаграмма токов и напряжений и результаты вычислений занесены с соответствующую таблицу.
В третьей части был проведен анализ трехфазной цепи по схеме Y. Были определены фазные токи, активная, реактивная и полная мощности каждой фазы, угол сдвига фаз между током и напряжением в каждой фазе. Была построена векторная диаграмма трехфазной цепи. Результаты расчетов были занесены в соответствующую таблицу.
 |
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ
 |
| 1. Атабеков Г. И. – Теоретические основы электротехники. Линейные электрические цепи. Изд. Лань, 2009. 592 с. [электронный ресурс] |
| 2. Бобровников Л. З., Электротехника: учебник для вузов Л. З. Бобровников.- 5-е издание, перераб. и доп.- СПБ.: Питер, 2004. – 560 с.:ил.-Мо |
| 3. Электротехника. В 3-х книгах: учеб. пособие для вузов. Кн. 2: Электрические машины. Промышленная электроника. Теория автомати- ческого управления под ред. П. А. Бутырина, Р. Х. Гафиятуллина, А. Л. Шес- такова. – Челябинск – М.:ЮУрГУ. 2004. – 711 с. |
| 4. Энциклопедия Mathcad.СОЛОН-Пресс, 2004. – 832 с.: ил. |
| 5. Бычков Ю. А., Золотницкий В. М., Чернышев Э. П. Основы теории электрических цепей. Лань, 2002. 464 с. 4. |
| 6. Бессонов Л. А. Теоретические основы электротехники. Электрические цепи. – М.: Высшая школа, 2000. |
| 7. Гилицкая Л.Н. Теоретические основы электротехники. Курсовое проектирование. Минск 1997. |
| 8. Махтанов П. Н. Основы анализа электрических цепей. Линейные цепи: Учеб. для электротех. Вузов. – 3-е изд., перераб. и доп. – М.: Высш. Шк., 1990. – 400 с. |
| 9. Зевеке Г. В., Ионкин П. А., Нетушил А. В., Страхов С. В. Основы теории цепей. – М.: Энергоатомиздат, 1989. |
| 10. Теоретическиеосновы электротехники. Учеб. для вузов. В трех т. Под общ. ред. К.М.Поливанова. Т.1. К.М.Поливанов. Линейные электрические цепи с сосредоточенными постоянными. –М.: Энергия- 1972. –240с. |






