Глава 2. Элементы векторной алгебры
Векторы
Определение 1. Вектор – это отрезок, имеющий определенную длину и направление. Если А – начало вектора, В – его конец, то вектор обозначается символом 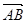 или
или  .
.
Вектор  называется противоположным вектору
называется противоположным вектору 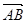 . Вектор, противоположный вектору
. Вектор, противоположный вектору  , обозначается -
, обозначается -  .
.
Определение 2. Длиной или модулем вектора 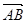 называется длина отрезка АВ и обозначается
называется длина отрезка АВ и обозначается 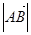 или
или 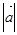 . Вектор, длина которого равна нулю, называется нулевым вектором и обозначается
. Вектор, длина которого равна нулю, называется нулевым вектором и обозначается  . Вектор, длина которого равна единице, называется единичным вектором и обозначается через
. Вектор, длина которого равна единице, называется единичным вектором и обозначается через  .
.
Определение 3. Векторы  и
и  называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. Коллинеарные векторы могут быть направлены одинаково или противоположно. Нулевой вектор коллинеарен любому вектору.
называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. Коллинеарные векторы могут быть направлены одинаково или противоположно. Нулевой вектор коллинеарен любому вектору.
Определение 4. Два вектора  и
и  называются равными (
называются равными ( =
=  ), если они коллинеарны, одинаково направлены и имеют одинаковые длины.
), если они коллинеарны, одинаково направлены и имеют одинаковые длины.
Определение 5. Три вектора в пространстве называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях.
Линейные операции над векторами.
Под линейными операциями над векторами понимают операции сложения и вычитания векторов, а также умножение вектора на число.
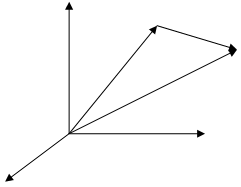
Пусть  и
и  - два произвольных вектора. Возьмем произвольную точку О и построим вектор
- два произвольных вектора. Возьмем произвольную точку О и построим вектор 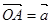 . От точки А отложим вектор
. От точки А отложим вектор  . Вектор
. Вектор 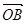 , соединяющий начало первого вектора с концом второго, называется суммой векторов
, соединяющий начало первого вектора с концом второго, называется суммой векторов  и
и  :
: 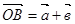 (рис. 1).
(рис. 1).

В

О А
Рис. 1.
Это правило сложения векторов называют правилом треугольника.
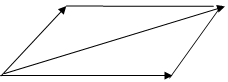
Сумму двух векторов можно построить также по правилу параллелограмма (рис. 2).
 А С
А С
О В
Рис. 2.
Под разностью векторов  и
и  понимается вектор
понимается вектор 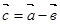 , такой, что
, такой, что  (рис.3).
(рис.3).
А
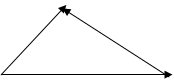
О В
Рис.3.
Произведением вектора  на число к называется вектор
на число к называется вектор 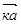 , который имеет длину
, который имеет длину 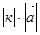 , коллинеарен вектору
, коллинеарен вектору  , имеет направление вектора
, имеет направление вектора  , если к > 0 и противоположное направление, если к < 0.
, если к > 0 и противоположное направление, если к < 0.
Линейные операции над векторами обладают следующими свойствами:
1.  =
= 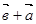 , 4.
, 4. 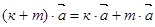 ,
,
1. ( ) +
) +  =
= 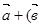 +
+  ), 5.
), 5. 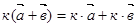 .
.
2. 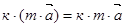 ,
,
Разложение вектора по координатным осям
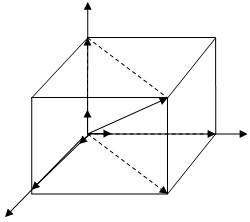 Рассмотрим в пространстве прямоугольную систему координат Оxyz. Выделим на координатных осях Ox, Oy, Oz единичные векторы
Рассмотрим в пространстве прямоугольную систему координат Оxyz. Выделим на координатных осях Ox, Oy, Oz единичные векторы  соответственно (рис. 4).
соответственно (рис. 4).
Выберем произвольный вектор  пространства и совместим его начало с началом координат:
пространства и совместим его начало с началом координат: 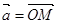 .
.
Найдем проекции вектора  на координатные оси.
на координатные оси.
Проведем через конец вектора  плоскости, параллельные координатным плоскостям.
плоскости, параллельные координатным плоскостям.
Рис. 4 Точки пересечения этих плоскостей с осями обозначим соответственно через М1, М2, М3. Получим прямоугольный параллелепипед. Ясно, что 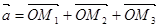 . Проекцией вектора
. Проекцией вектора  на ось Ox является отрезок
на ось Ox является отрезок  , на Oy -
, на Oy -  , на Oz -
, на Oz - 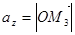 .
.
Тогда вектор  может быть представлен в виде
может быть представлен в виде  . Такое представление называется разложением вектора
. Такое представление называется разложением вектора  по осям координат, или разложением по ортам.
по осям координат, или разложением по ортам.
Числа 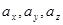 называются координатами вектора
называются координатами вектора  . Пишут
. Пишут  = (
= (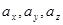 ).
).
Зная координаты вектора  , легко найти его модуль:
, легко найти его модуль: 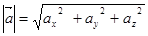 .
.
Если вектор  составляет с осями координат углы
составляет с осями координат углы 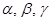 , то можно найти, что
, то можно найти, что 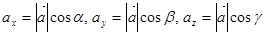 .
.
Отсюда
 .
.
Числа 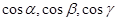 называются направляющими косинусами вектора
называются направляющими косинусами вектора  . Они связаны соотношением
. Они связаны соотношением
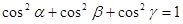 .
.
Пусть даны два вектора  = (
= (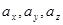 ),
),  = (
= (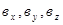 ), тогда:
), тогда:
1.  ;
;
2. 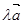 = (
= ( );
);
3.  =
= 
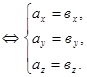
4. Вектор  коллинеарен вектору
коллинеарен вектору  тогда и только тогда, когда выполняется условие
тогда и только тогда, когда выполняется условие 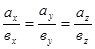 , т.е. координаты коллинеарных векторов пропорциональны. Верно и обратное: векторы, имеющие пропорциональные координаты, коллинеарны.
, т.е. координаты коллинеарных векторов пропорциональны. Верно и обратное: векторы, имеющие пропорциональные координаты, коллинеарны.
 5. Пусть в пространстве задана прямоугольная система координат Оxyz. Вектор
5. Пусть в пространстве задана прямоугольная система координат Оxyz. Вектор  , начало которого находится в начале координат, а конец в точке М (x,y,z) называется радиусом-вектором точки М и обозначается
, начало которого находится в начале координат, а конец в точке М (x,y,z) называется радиусом-вектором точки М и обозначается 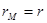 , причем
, причем 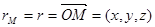 .
.
Рис. 5. Тогда если известны координаты точек  , то
, то 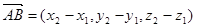 (рис. 5).
(рис. 5).
Следовательно, координаты вектора равны разностям соответствующих координат его конца и начала.
Пример 1. Даны координаты вершин Δ АВС: А (1;2;3), В (3;2;1), С (1;4;1). Показать, что Δ АВС – равносторонний.
Решение: Найдем координаты векторов 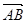 ,
,  ,
, 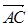 . Получим
. Получим
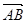 = (3-1, 2-2, 1-3) = (2, 0, -2),
= (3-1, 2-2, 1-3) = (2, 0, -2),  = (-2, 2, 0),
= (-2, 2, 0), 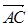 = (0, 2, -2). Вычислим длины данных векторов. Имеем
= (0, 2, -2). Вычислим длины данных векторов. Имеем 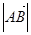 =
=  ,
,  =
= 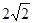 ,
, 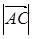 =
= 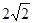 . Так как
. Так как 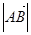 =
=  =
= 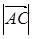 , то Δ АВС – равносторонний.
, то Δ АВС – равносторонний.






