1–10. На телефонной станции проводились наблюдения над числом X неправильных соединений в сутки. Результаты наблюдений представлены в виде табл. 1. Наблюдения проводились в течение 20 рабочих дней. Провести статистическую обработку результатов наблюдения, а именно:
1) составить вариационный ряд;
2) составить таблицу распределения частот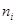 
и относительных частот 
;
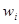3) построить полигон частот и гистограмму частостей;
4) определить выборочные характеристики средней величины: моду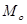 
, медиану 
, среднее значение 
;
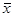5) определить выборочные характеристики неравномерности ежедневного числа неправильных телефонных соединений: размах R, дисперсию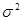 
, среднее квадратическое отклонение 
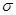, коэффициент вариации V;
6) записать точечные оценки генеральной средней и генеральной дисперсии.
7) составить эмпирическую функцию распределения 
ежедневного числа неправильных телефонных соединений и построить ее график.
Таблица 1
| День | Число неправильных телефонных соединений за сутки | |||||||||
| № варианта | ||||||||||
11–20. По данному (табл. 2) интервальному распределению значений признака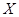 
некоторой выборочной совокупности необходимо:
1) построить гистограмму относительных частот;
2) найти выборочные характеристики распределения (среднее значение, моду, медиану, размах, дисперсию, среднее квадратическое отклонение, коэффициент вариации).
Таблица 2
| Вариант | ||||
| Номер интервала | Границы интервалов | Интервальные частоты | Границы интервалов | Интервальные частоты |
| 147–155 | 50 – 62 | |||
| 155 – 163 | 62 – 74 | |||
| 163 – 171 | 74 – 86 | |||
| 171 – 179 | 86 – 98 | |||
| 179 – 187 | 98 – 110 | |||
| 187 – 195 | 110 – 122 | |||
| Вариант | ||||
| Номер интервала | Границы интервалов | Интервальные частоты | Границы интервалов | Интервальные частоты |
| 15,6 – 17 | 35,2 – 39,2 | |||
| 17 – 18,4 | 39,2 – 43,2 | |||
| 18,4 – 19,8 | 43,2 – 47,2 | |||
| 19,8 – 21,2 | 47,2 – 51,2 | |||
| 21,2 – 22,6 | 51,2 –55,2 | |||
| 22,6 – 24 | 55,2 –59,2 | |||
| Вариант | ||||
| Номер интервала | Границы интервалов | Интервальные частоты | Границы интервалов | Интервальные частоты |
| 51–65 | 88,4–90,0 | |||
| 65–79 | 90–91,6 | |||
| 79–93 | 91,6–93,2 | |||
| 93–107 | 93,2–94,8 | |||
| 107–121 | 94,8–96,4 | |||
| 121–135 | 96,4–98,0 |
| Вариант | ||||
| Номер интервала | Границы интервалов | Интервальные частоты | Границы интервалов | Интервальные частоты |
| 0,56–0,58 | 24–28 | |||
| 0,58–0,60 | 28–32 | |||
| 0,60–0,62 | 32–36 | |||
| 0,62–0,64 | 36–40 | |||
| 0,64–0,66 | 40–44 | |||
| 0,66–0,68 | 44–48 | |||
| Вариант | ||||
| Номер интервала | Границы интервалов | Интервальные частоты | Границы интервалов | Интервальные частоты |
| 430–490 | 7,45–8,25 | |||
| 490–550 | 8,25–9,05 | |||
| 550–610 | 9,05–9,85 | |||
| 610–670 | 9,85–10,65 | |||
| 670–730 | 10,65–11,45 | |||
| 730–790 | 11,45–12,25 |
21–30. По данным таблицы 2 требуется:
1) используя критерий 
-Пирсона, при уровне значимости 
проверить гипотезу о том, что случайная величина X – время, проводимое студентами в Интернете в неделю – распределена по нормальному закону, записать функцию соответствующего нормального распределения;
2) определить границы, в которых с вероятностью 0,95 заключено среднее время, проводимое студентами в Интернете в неделю;
3) определить объем выборки (число студентов, которых нужно опросить), при котором те же границы для среднего времени, проводимого студентами в Интернете в неделю, можно гарантировать с вероятностью 0,99.
31–40. Проведены исследования 200 семей некоторого района по двум показателям (признакам): Х – расходы на питание (% от общего дохода семьи); У – доходы семьи (тыс. руб.). По данным двумерной таблицы распределения (табл. 3) требуется:
1) вычислить условные средние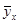 
, построить эмпирическую линию регрессии;
2) предполагая, что между переменными X и Y существует линейная корреляционная зависимость:
а) вычислить коэффициент корреляции 
и сделать вывод о тесноте и направлении связи между переменными X и Y;
б) найти уравнение прямой регрессии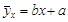 
, построить график этой прямой на одном чертеже с эмпирической линией регрессии.
Таблица 3
уj
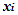
| уj
| ||||||||||
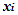
| уj
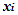
| уj
| ||||||||||
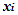
| уj
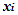
| уj
| ||||||||||
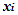
| уj
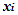
| уj
| ||||||||||
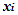
| уj
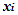
| уj
| ||||||||||
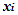
Численные методы
41–50. В табл. 4 приведены аргументы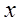 
и значения 
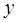некоторой функции.
Требуется:
1) методом наименьших квадратов найти наилучшие значения параметров 
и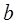 
в уравнении прямой 
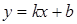, аппроксимирующей заданную функцию;
2) для заданной функции построить интерполяционный многочлен Лагранжа;
3) на одной координатной плоскости построить точки 
и полученные в пунктах 1 и 2 прямую и параболу (параболу – схематично или выполнить построение в среде MathCAD).
Таблица 4
| № задачи | ||||||||||||||||||||
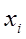
| -1 | -2 | -1 | |||||||||||||||||
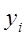
| -9 | -3 | -3 | -8 | -9 | -8 | ||||||||||||||
| № задачи | ||||||||||||||||||||
|
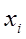
| -1 | -2 | -3 | -1 | ||||||||||||||||
|
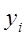
| -5 | -2 | -8 | -4 |
Список рекомендуемой литературы
1. Письменный Д. Т. Конспект лекций по теории вероятностей, математической статистике и случайным процессам / Д. Т. письменный. – М.: АЙРИС ПРЕСС, 2006.
2. Кремер Н. Ш. Теория вероятностей и математическая статистика / Н. Ш. Кремер. – М.: ЮНИТИ, 2006.
3. Общая теория статистики: статистическая методология в изучении коммерческой деятельности: учебник / под ред. О. Э. Башиной, А. А. Спирина. – М.: Финансы и статистика, 2006.
4. Гмурман В. Е. Теория вероятностей и математическая статистика / В. Е. Гмурман. – М.: Высшая школа, 1998.
5. Гмурман В. Е. Руководство к решению задач по теории вероятностей и математической статистике / В. Е. Гмурман. – М.: Высшая школа, 1998.
6. Копченова Н. В. Вычислительная математика в примерах и задачах: учеб. пособие для технич. и эконом. вузов / Н. В. Копченова, И. А. Марон – СПб.: Лань, 2009.
Следующие пособия, изданные кафедрой высшей математики КГТУ,
помогут вам выполнить контрольные работы:
7. Секованова Л. А. Сборник заданий к типовому расчету по математической статистике / Л. А. Секованова, Т. А. Андревкина, О. В. Назарова. – Кострома: Изд-во Костром. гос. технол. ун-та, 2010.
8. Землякова И.В. Математическая статистика. Теория и практика / И.В. Землякова, О.Б. Садовская, А.В. Чередникова. – Кострома: Изд-во Костром. гос. технол. ун-та, 2010.
Интернет-ресурс:
Образовательные ресурсы Интернета – Математика [Электронный ресурс]. – Режим доступа: http://www.alleng.ru/edu/math1.htm
ПРИЛОЖЕНИЕ 1
Таблица значений функции Лапласа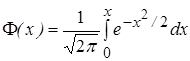 
| x | F(x) | x | F(x) | x | F(x) | x | F(x) | x | F(x) | ||
| 0,00 | 0,0000 | 0,44 | 0,1700 | 0,88 | 0,3106 | 1,32 | 0,4066 | 1,76 | 0,4608 | ||
| 0,01 | 0,45 | 0,89 | 1,33 | 1,77 | |||||||
| 0,02 | 0,46 | 0,90 | 1,34 | 1,78 | |||||||
| 0,03 | 0,47 | 0,91 | 1,35 | 1,79 | |||||||
| 0,04 | 0,48 | 0,92 | 1,36 | 1,80 | |||||||
| 0,05 | 0,49 | 0,93 | 1,37 | 1,81 | |||||||
| 0,06 | 0,50 | 0,94 | 1,38 | 1,82 | |||||||
| 0,07 | 0,51 | 0,95 | 1,39 | 1,83 | |||||||
| 0,08 | 0,52 | 0,96 | 1,40 | 1,84 | |||||||
| 0,09 | 0,53 | 0,97 | 1,41 | 1,85 | |||||||
| 0,10 | 0,54 | 0,98 | 1,42 | 1,86 | |||||||
| 0,11 | 0,55 | 0,99 | 1,43 | 1,87 | |||||||
| 0,12 | 0,56 | 1,00 | 1,44 | 1,88 | |||||||
| 0,13 | 0,57 | 1,01 | 1,45 | 1,89 | |||||||
| 0,14 | 0,58 | 1,02 | 1,46 | 1,90 | |||||||
| 0,15 | 0,59 | 1,03 | 1,47 | 1,91 | |||||||
| 0,16 | 0,60 | 1,04 | 1,48 | 1,92 | |||||||
| 0,17 | 0,61 | 1,05 | 1,49 | 1,93 | |||||||
| 0,18 | 0,62 | 1,06 | 1,50 | 1,94 | |||||||
| 0,19 | 0,63 | 1,07 | 1,51 | 1,95 | |||||||
| 0,20 | 0,64 | 1,08 | 1,52 | 1,96 | |||||||
| 0,21 | 0,65 | 1,09 | 1,53 | 1,97 | |||||||
| 0,22 | 0,66 | 1,10 | 1,54 | 1,98 | |||||||
| 0,23 | 0,67 | 1,11 | 1,55 | 1,99 | |||||||
| 0,24 | 0,68 | 1,12 | 1,56 | 2,00 | |||||||
| 0,25 | 0,69 | 1,13 | 1,57 | 2,01 | |||||||
| 0,26 | 0,70 | 1,14 | 1,58 | 2,04 | |||||||
| 0,27 | 0,71 | 1,15 | 1,59 | 2,06 | |||||||
| 0,28 | 0,72 | 1,16 | 1,60 | 2,08 | |||||||
| 0,29 | 0,73 | 1,17 | 1,61 | 2,10 | |||||||
| 0,30 | 0,74 | 1,18 | 1,62 | 2,12 | |||||||
| 0,31 | 0,75 | 1,19 | 1,63 | 2,14 | |||||||
| 0,32 | 0,76 | 1,20 | 1,64 | 2,16 | |||||||
| 0,33 | 0,77 | 1,21 | 1,65 | 2,18 | |||||||
| 0,34 | 0,78 | 1,22 | 1,66 | 2,20 | |||||||
| 0,35 | 0,79 | 1,23 | 1,67 | 2,22 | |||||||
| 0,36 | 0,80 | 1,24 | 1,68 | 2,24 | |||||||
| 0,37 | 0,81 | 1,25 | 1,69 | 2,2 | |||||||
| 0,38 | 0,82 | 1,26 | 1,70 | 2,28 | |||||||
| 0,39 | 0,83 | 1,27 | 1,71 | 2,30 | |||||||
| 0,40 | 0,84 | 1,28 | 1,72 | 2,32 | |||||||
| 0,41 | 0,85 | 1,29 | 1,73 | 2,34 | |||||||
| 0,42 | 0,86 | 1,30 | 1,74 | 2,36 | |||||||
| 0,43 | 0,87 | 1,31 | 1,75 | 2,38 | |||||||
| x | F(x) | x | F(x) | x | F(x) | x | F(x) | ||||
| 2,40 | 0,4918 | 2,60 | 0,4953 | 2,80 | 0,4974 | 3,00 | 0,49865 | ||||
| 2,42 | 2,62 | 2,82 | 3,20 | 0,49931 | |||||||
| 2,44 | 2,64 | 2,84 | 3,40 | 0,49966 | |||||||
| 2,46 | 2,66 | 2,86 | 3,60 | 0,499841 | |||||||
| 2,48 | 2,68 | 2,88 | 3,80 | 0,499928 | |||||||
| 2,50 | 2,70 | 2,90 | 4,00 | 0,499968 | |||||||
| 2,52 | 2,72 | 2,92 | 4,50 | 0,499997 | |||||||
| 2,54 | 2,74 | 2,94 | 5,00 | 0,499997 | |||||||
| 2,56 | 2,76 | 2,96 | |||||||||
| 2,58 | 2,78 | 2,98 | |||||||||
ПРИЛОЖЕНИЕ 2
Критические точки распределения c2
| Число степеней свободы k | Уровень значимости a | |||||
| 0,010 | 0,025 | 0,050 | 0,950 | 0,975 | 0,990 | |
| 6,60000 | 5,00000 | 3,80000 | 0,00390 | 0,00098 | 0,00016 | |
| 9,20000 | 7,40000 | 6,00000 | 0,10300 | 0,05100 | 0,02000 | |
| 11,30000 | 9,40000 | 7,80000 | 0,35200 | 0,21600 | 0,11500 | |
| 13,30000 | 11,10000 | 9,50000 | 0,71100 | 0,48400 | 0,29700 | |
| 15,10000 | 12,80000 | 11,10000 | 1,15000 | 0,83100 | 0,55400 | |
| 16,80000 | 14,40000 | 12,60000 | 1,64000 | 1,24000 | 0,87200 | |
| 18,50000 | 16,00000 | 14,10000 | 2,17000 | 1,69000 | 1,24000 | |
| 20,10000 | 17,50000 | 15,50000 | 2,73000 | 2,18000 | 1,65000 | |
| 21,70000 | 19,00000 | 16,90000 | 3,33000 | 2,70000 | 2,09000 | |
| 23,20000 | 20,50000 | 18,30000 | 3,94000 | 3,25000 | 2,56000 | |
| 24,70000 | 21,90000 | 19,70000 | 4,57000 | 3,82000 | 3,05000 | |
| 26,20000 | 23,30000 | 21,00000 | 5,23000 | 4,40000 | 3,57000 | |
| 27,70000 | 24,70000 | 22,40000 | 5,89000 | 5,01000 | 4,11000 | |
| 29,10000 | 26,10000 | 23,70000 | 6,57000 | 5,63000 | 4,66000 | |
| 30,60000 | 27,50000 | 25,00000 | 7,26000 | 6,26000 | 5,23000 | |
| 32,00000 | 28,80000 | 26,30000 | 7,96000 | 6,91000 | 5,81000 | |
| 33,40000 | 30,20000 | 27,60000 | 8,67000 | 7,56000 | 6,41000 | |
| 34,80000 | 31,50000 | 28,90000 | 9,39000 | 8,23000 | 7,01000 | |
| 36,20000 | 32,90000 | 30,10000 | 10,10000 | 8,91000 | 7,63000 | |
| 37,60000 | 34,20000 | 31,40000 | 10,90000 | 9,59000 | 8,26000 | |
| 38,90000 | 35,50000 | 32,70000 | 11,60000 | 10,30000 | 8,90000 | |
| 40,30000 | 36,80000 | 33,90000 | 12,30000 | 11,00000 | 9,54000 | |
| 41,60000 | 38,10000 | 35,20000 | 13,10000 | 11,70000 | 10,20000 | |
| 43,00000 | 39,40000 | 36,40000 | 13,80000 | 12,40000 | 10,90000 | |
| 44,30000 | 40,60000 | 37,70000 | 14,60000 | 13,10000 | 11,50000 | |
| 45,60000 | 41,90000 | 38,90000 | 15,40000 | 13,80000 | 12,20000 | |
| 47,00000 | 43,20000 | 40,10000 | 16,20000 | 14,60000 | 12,90000 | |
| 48,30000 | 44,50000 | 41,30000 | 16,90000 | 15,30000 | 13,60000 | |
| 49,60000 | 45,70000 | 42,60000 | 17,70000 | 16,00000 | 14,30000 | |
| 50,90000 | 47,00000 | 43,80000 | 18,50000 | 16,80000 | 15,00000 |
