Анализ экспериментальных данных

Содержание

1. Введение --------------------------------------------------------------------------------------------3

2. Оптическая модель ядра---------------------------------------------------------------------- 4

3. Анализ экспериментальных данных ------------------------------------------------------6

4. Заключение --------------------------------------------------------------------------------------10

5. Использованные литературы ---------------------------------------------------------------11

Введение

В данной работе предоставлены краткое изложение теории оптического потенциала упругого рассеяния и результаты выполненной работы по упругому рассеянию в рамках оптической модели. Процесс реакции упругого рассеяния рассматривается на примере ²³Na+ ¹n, E_lab = 5.44 МэВ .

Задачи курсовой работы:

· Взять данные на сайте (http://cdfe.sinp.msu.ru/services/unifsys/index.html) или (http://nrv.jinr.ru/nrv ) и оцифровать данные;

· На основе имеющихся данных по упругому рассеянию ядер, используя сервис http://nrv.jinr.ru/nrv, позволяющий описать реакции, выполнить расчет дифференциального сечения реакции, а также сравнить экспериментальные и расчетные кривые, добиться их совпадения.

 

 

Оптическая модель ядра

В квантовомеханической оптической модели упругого рассеяния (ОМ) относительное движение частицы описывается с помощью одночастичного уравнения Шредингера:

,

где E = ²k²/2 – энергия относительного движения, – приведенная масса, V_OM эффективный неэрмитовый оператор, который называется оптическим потенциалом (ОП). Предполагается, что влияние всех каналов реакции на упругий канал может быть учтено соответствующим выбором ОП. На практике обычно используется феноменологический ОП с простой радиальной зависимостью:

VOM(r) = Vc(r) + VN(r) + iW(r) + [Vso(r) + iWso(r)]( · ).

(

Здесь кулоновское и ядерное взаимодействие Vc + V_N такое же, как и в классической модели. Мнимая часть ОП может иметь поверхностную или объемную компоненты, либо их суперпозицию. Спин-орбитальное взаимодействие V_so + iW_so может быть включено в случае, если рассеимая частица имеет не равный 0 спин.
Волновая функция относительного движения имеет граничное условие на бесконечности:

,

где f() - это амплитуда рассеяния (при рассеянии заряженных частиц эта формула может быть немного модифицирована с учетом искажений плоской и сферической волн на больших расстояниях дальнодействующим кулоновским взаимодействием). Чтобы найти амплитуду рассеяния, полная волновая функция представляется в виде разложения по парциальным волнам:

= (2l + 1)il l(r)Pl(cos )

(

и одномерные радиальные уравнения Шрёдингера численно интегрируются от 0 до некоторого достаточно большого r = R_max, где V_N(r) и W(r) можно пренебречь и остается только кулоновское взаимодействие.

На таких больших расстояниях численное решение плавно переходит в известное асимптотическое поведение парциальных волн:

l(r) [(Fl + iGl) + Sl(Fl - iGl)],

где F_l и G_l -это действительная и мнимая части парциальной кулоновской волновой функции.Имея найденные таким образом S-матричные элементы, можно рассчитать амплитуду рассеяния с помощью (5) и дифференциальное сечение упругого рассеяния с помощью (6).
Для более глубокого понимания механизма упругого рассеяния (природу интеренференционной структуры, радужные эффекты и т.д.) классическая и квазиклассическая модели могут использоваться совместно с рассчётами по ОМ.
С оптической моделью также может быть сделано так называемое “near-far” разбиение амплитуды рассеяния, которое даёт во многих случаях лучшее понимание некоторых спецефических особенностей углового расспределения [1,2]. Такое разбиение идентично преобразованию формулы (5), основанному на представлении полиномов Лагранжа в виде:

Pl(cos ) = () + ()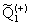

(

с асимптотикой

() [ (2l + 1)sin ]^-1/2exp{i[ + (l + 1/2) /4]}, при l >> 1/sin .

Подставляяя (13) в (5) получаем “ near-far ” разбиение, которое показывает в коротко-волновом приближении (L_max = kR_max >> 1) вклады в амплитуду, которые даёт рассеяние
на положительные ("near", 2d _l/dl = (b) = + ) и отрицательные ("far", 2d _l/dl = (b) = - ) углы.

Типичный оптический потенциал содержит 9 геометрических параметров (R_v, R_ws, R_wv, R_sl, R_c, a_v, a_ws, a_wv, a_sl) и 5 энергетических (V₀, W_s, W_v, V_sl, W_sl). Значения этих параметров подбираются так, чтобы дифференциальные сечения упругого рассеяния и поляризации, расчитанные по оптической модели хорошо согласовывались с экспериментом. Так как оптический потенциал является усредненной характеристикой взаимодействия, то следует ожидать плавную зависимость параметров оптического потенциала от характеристик ядер и энергии. Так параметры R_i ~ r_0iA^1/3, параметры диффузности a_i не должны зависеть от массового числа. Систематизация оптических параметров, полученных из экспериментов при различных энергиях и на разных ядрах, позволила получить феноменологические зависимости для параметров, получить наборы так называемых глобальных параметров.

Для заданных ОМ параметров код NRV оптической модели позволяет рассчитать, представить в графической и табличной форме, все выше упомянутые величины: парциальные волны _l(r), парциальные матричные элементы S_l, полную трехмерную волновую функцию (r, ) и дифференциальное сечение рассеяния d /d . Автоматический поиск параметров ОМ может быть выполнен фитированием расчетного углового распределения к экспериментальным данным.Многие другие дополнительные возможности также включены в код, что позволяет анализировать исследуемый процесс в деталях.

Анализ экспериментальных данных

Для описания реакции упругого рассеяния применилась оптическая модель ядра. В качестве примера рассмотрим реакцию столкновения нейтрона ¹n с натрий ²³Na.

Графики экспериментальных данных зависимости сечения реакции ²³Na+ ¹n, Е_lab=52МэВ от угла были взяты из статьи F.G.PEREY,W.E.KINNEY/Neutron elastic- and inelastic- scattering cross 6 sections for Na in the range of 5.4 to 8.5 MeV. [3]

Рисунок 1: Дифференциальное сечение реакции ²³Na + ¹n, E_lab = 5.44 МэВ.

Обработка данных и определение параметров реакции проводилась с помощью раздела «Elastic scattering», размещённого на сайте http://nrv.jinr.ru/nrv/. Главное диалоговое окно сервиса приведено на рисунке 2.

Рисунок 2: Рабочее окно "Elastic scattering"

Первоначальная картинка с необработанными данными выглядела таким образом(Рисунок 3):

Рисунок 3. График зависимости дифференциального сечения от угла рассеяния (необработанные данные).

Как показано на рисунке 3, теоретические и экспериментальные данные лежат на одном уровне, но в рамках оптической модели они недостаточно хорошо описаны.

Экспериментальные значения параметров были взяты из работы [3](таблица 1) и дали качественное совпадение с экспериментальными данными.

Таблица 1

 

ANG-CM, ADEG	DATA, MB/SR	DATA-ERR, PER-CENT
28.65	334.86	6.1
33.32	250.96	6.1
33.33	239.62	6.1
39.02	183.6	6.1
39.03	187.19	6.1
43.68	128.68	6.2
44.71	132.77	6.2
49.34	98.47	4.3
55.01	64.41	6.3
59.12	52.87	6.3
64.74	42.78	6.3
70.34	37.17	6.3
74.38	39.86	4.7
79.94	39.56	5.8
85.48	44.51	4.7
90.51	33.89	5.2
101.49	33.37
104.45	30.48	4.8

Таблица 1: Экспериментальные данные из работы [3].

Таблица 2

Потенциал	Значения параметров
Реальная часть	V0=- 100 МэВ r0= 1.2844 fm aV = 0,6 fm
Мнимая часть	W0=-10 MэВ r 0= 1.2844 fm aw = 0.6 fm
σR, mb	931.67
σtot, mb	2127.99
χ2 / N points	110.683

 

Таблица 2: Начальные параметры потенциалов.

 

Параметры были изменены на следующие значения показанные в таблице 3.

Таблица 3

 

Потенциал	Значения параметров
Реальная часть	V0=- 122,245 МэВ r0= 1.28 fm aV = 0.434 fm
Мнимая часть	W0=3,154 MэВ r 0= 1.2844 fm aw = 0.6 fm
σR, mb	749.15
σtot, mb	1856.32
χ2 / N points	1.951

 

Таблица 3. Подобранные параметры.

После чего график зависимости дифференциального сечения упругого рассеяния от угла рассеяния изменился следующим образом(Рисунок 4):

 

 

Рисунок 4. График зависимости дифференциального сечения реакции от угла рассеяния.

По этой картинке видно, что совпадение теоретической и экспериментальной кривых зависимости сечения от угла на достаточно хорошем уровне.

В работе реальная и мнимая части потенциала берутся в виде потенциала Вудса-Саксона, описывающего упругое рассеяние ¹n на ²³Na:

 

(6)

Заключение

В ходе курсовой работы была изучена оптическая модель упругого рассеяния в реакции ²³Na+ ¹n, E_lab = 5.44 МэВ. Были подобраны параметры реальной и мнимой частей оптического потенциала, описывающих экспериментальные данные на достаточно неплохом уровне.

Была рассмотрена работа зарубежных авторов F.G.PEREY,W.E.KINNEY/Neutron elastic- and inelastic- scattering cross 6 sections for Na in the range of 5.4 to 8.5 MeV на сайте http://cdfe.sinp.msu.ru/services/unifsys/index.html

 

 

Использованные литературы:

1. R.S. Fuller, Phys.Rev., C12 (1975) 1561.

2. M.S. Hussein, K.W.McVoy, Progr.Part.Nucl.Phys, 12 (1984) 103.

3. http://cdfe.sinp.msu.ru/cgi-bin/exf2htm?LINK=10104002&SOURCE=ON

4. Семкин, В.Загребаев, Izv. AN, ser.fiz, 58 (1994), 109

5. V.I. Zagrebaev, AnnPhys.(N.Y.), 197 (1990) 33.