Розрахунок усталених режимів в нелінійних
Електричних колах методом контурних струмів числовими методами
Методичні вказівки
до практичних занять та лабораторних робіт
з дисциплін “Математичне моделювання в електроенергетиці” та “Математичні моделі в електротехніці” для студентів електроенергетичних спеціальностей
Затверджено на засіданні
кафедри «Електричні станції»
Протокол № 1 від 28 серпня 2013 р.
Львів 2014
Розрахунок усталених режимів в нелінійних електричних колах методом контурних струмів числовими методами. Методичні вказівки до практичних занять та лабораторних робіт з дисциплін “Математичне моделювання в електроенергетиці” та “Математичні моделі в електротехніці” / Укл. М.С. Сегеда, Т.А. Мазур – Львів: Національний університет “Львівська політехніка”, 2014. – 25 с.
Укладачі: Сегеда М.С., професор, доктор техн. наук
Мазур Т.А., асистент
Відповідальний за випуск: Сегеда М.С., професор, доктор техн. наук
Рецензенти: Варецький Ю.О., професор, доктор техн. наук
Гоголюк П.Ф., доцент, канд. техн. наук
Мета роботи: вивчення числових методів розв’язання системи нелінійних скінчених рівнянь числовими методами; оволодіти навиками використання системи символьної математики МаthCad.
Короткі теоретичні відомості
У задачах електроенергетики система скінченних рівнянь у загальному випадку нелінійна. Методи розв’язання системи нелінійних скінченних рівнянь можна розглядати як узагальнення відповідних методів розв'язання системи лінійних рівнянь, що з дидактичного погляду має значні переваги.
Одним з найбільш перспективних методів аналізу електромагнетних процесів електричних кіл є метод контурних координат, особливо за великої кількості взаємо індуктивно-зв’язаних віток. Важливою умовою ефективності цього методу являється формування математичної моделі електричної системи на підставі оптимальної системи незалежних контурів, яка забезпечує максимальну розрідженість її матриці контурних параметрів.
Приклади розрахунку
Розрахувати усталений режим в нелінійному електричному колі постійного струму (рис. 1) методом контурних струмів.

Рис. 1. Схема електричного кола
Дані: 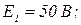
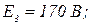
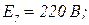
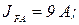



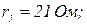

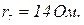
Вольт-амперна характеристика нелінійних резисторів першої та четвертої віток показано на рис. 2.

Рис. 2. Вольт-амперна характеристика нелінійних резисторів
Розв’язати систему скінчених нелінійних рівнянь числовими методами: простої ітерації; ітерації Зайделя; найшвидшого спуску (градієнтний метод); Ньютона-Рафсона. Похибка розрахунку 
Розв’язання.
позначаємо умовні напрями струмів в електричному колі (рис. 1) схема якого наведена рис. 3. Схема (рис. 3) має 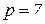 віток,
віток, 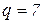 вузлів та
вузлів та 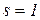 електрично не зв’язаних схем.
електрично не зв’язаних схем.

Рис. 3. Схема електричного кола
Граф схеми електричного кола зображено на рис. 4. вузол 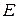 приймаємо за базовий. Вузли
приймаємо за базовий. Вузли 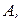

 та
та 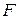 є елементарні. Вітки з нелінійними опорами відтворюємо хордами.
є елементарні. Вітки з нелінійними опорами відтворюємо хордами.
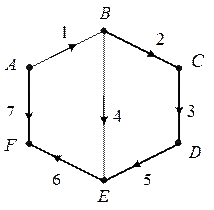
Рис. 4. Граф схеми електричного кола
Рівняння методу контурних струмів
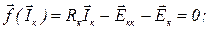

де 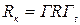 - (п´п)- вимірна матриця контурних опорів;
- (п´п)- вимірна матриця контурних опорів; 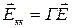 - п -вимірний вектор-стовпець контурних ЕРС, зумовлених ЕРС віток;
- п -вимірний вектор-стовпець контурних ЕРС, зумовлених ЕРС віток;  - п -вимірний вектор-стовпець контурних ЕРС, зумовлених ДС;
- п -вимірний вектор-стовпець контурних ЕРС, зумовлених ДС; 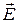 - п -вимірний вектор-стовпець ЕРС віток;
- п -вимірний вектор-стовпець ЕРС віток;  - (q-s) - вимірний вектор-стовпець ДС;
- (q-s) - вимірний вектор-стовпець ДС;  - матриця коефіцієнтів розподілу дерева;
- матриця коефіцієнтів розподілу дерева;  - субматриця сполучення дерева.
- субматриця сполучення дерева.
Формуємо матриці, які описують граф.
Матриця сполучення

Субматриця сполучення дерева
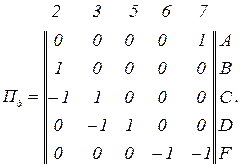
Обернену субматрицю сполучення дерева отримуємо на підставі формування матриці коефіцієнтів розподілу дерева, тобто

Матриця контурів

Матриця опорів

Матриця коефіцієнтів розподілу дерева
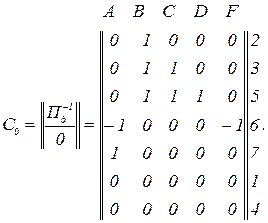
Вектор ЕРС
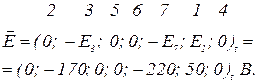
Вектор джерел струму
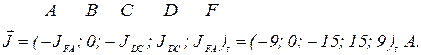
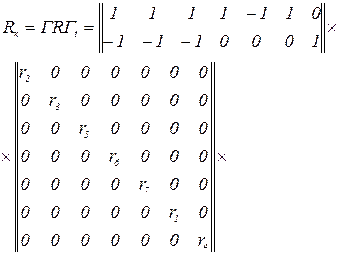

Вектор контурних ЕРС

Вектор контурних ЕРС, зумовлених ДС
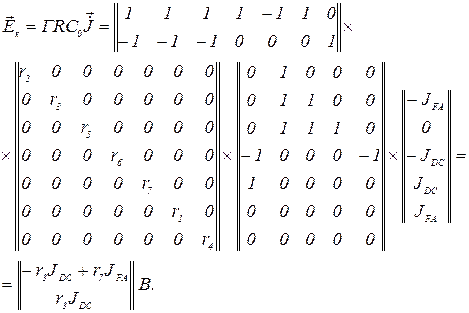
Апроксимацію вольт-амперної характеристики нелінійних резисторів першої та четвертої віток здійснюємо використовуючи метод підставлення за таким поліномом

Для визначення параметрів апроксимуючого полінома візьмемо три точки на кривій (рис. 2), тобто 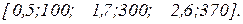
Підставляючи в апроксимуючий поліном значення заданої множини точок отримуємо систему рівнянь у матрично-векторній формі
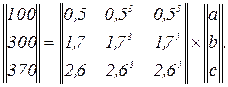
Використовуючи систему символьної математики МаthCad обчислюємо коефіцієнти 
Запишемо в розгорнутій формі систему нелінійних рівнянь
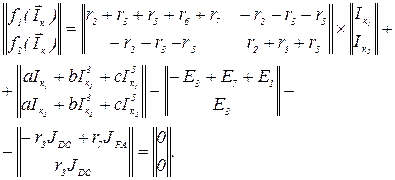
В отриману систему рівнянь підставляємо значення параметрів та фізичних величин

Для знаходження нульового наближення контурних струмів, в апроксимуючому поліномі вольт-амперної характеристики візьмемо лише лінійні члени, тобто  і систему рівнянь розв’яжемо як лінійну, тобто
і систему рівнянь розв’яжемо як лінійну, тобто

Використовуючи систему символьної математики МаthCad обчислюємо 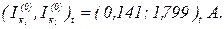
Метод простої ітерації.
Рекурентна формула методу простої ітерації

Матриця Якобі визначається за виразом

Для нульового наближення контурних струмів, які обчислено попередньо, тобто  , отримуємо матрицю Якобі
, отримуємо матрицю Якобі

 Для обчислення першого наближення контурних струмів обчислюємо вектор нев’язок для нульового наближення, тобто
Для обчислення першого наближення контурних струмів обчислюємо вектор нев’язок для нульового наближення, тобто  Перше наближення контурних струмів
Перше наближення контурних струмів
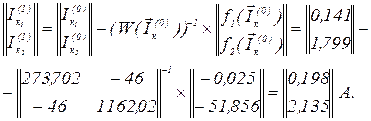
Перевірка точності  , тобто
, тобто

Використовуючи систему символьної математики МаthCad в ітераційному циклі обчислюємо контурні струми з точністю  кількість ітерацій
кількість ітерацій  контурні струми
контурні струми 
Метод ітерації Зайделя.
У методі ітерації Зайделя, значення наближених „молодших” невідомих, знайдених на даному кроці, використовується для визначення старших невідомих на тому самому кроці наближення, тобто для обчислення  використовується
використовується 
У розгорнутій формі записуємо рівняння

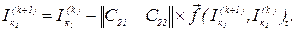
Перша ітерація.
Нульові наближення обчисленні у методі простої ітерації, тобто 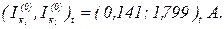
Обчислюємо матрицю  , тобто
, тобто
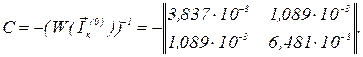
Вектор нев’язок обчислюємо як і у методі простої ітерації, тобто


Обчислюємо перше наближення першого контурного струму
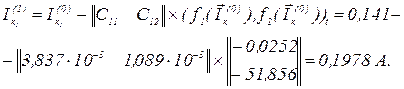
Вектор нев’язок для другого контурного струму з врахуванням 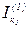

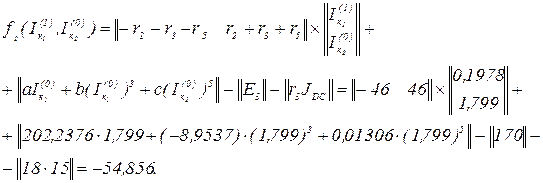
Обчислюємо перше наближення другого контурного струму

Перевірка точності  , тобто
, тобто

Використовуючи систему символьної математики МаthCad в ітераційному циклі обчислюємо контурні струми з точністю  кількість ітерацій
кількість ітерацій  контурні струми
контурні струми 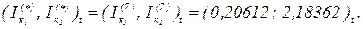
Метод найшвидшого спуску (градієнтний метод).
Для обчислення контурних струмів на 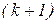 кроці необхідно виконати такі операції:
кроці необхідно виконати такі операції:
1) обчислити вектор нев’язок

2) визначити вектор

3) обчислити вектор

4) знайти параметр ітерації
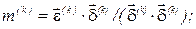
5) визначити 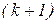 -е наближення вектора контурних струмів
-е наближення вектора контурних струмів
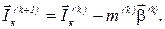
В методі простої ітерації обчислено нульове наближення контурних струмів 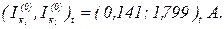
матриця Якобі для нульового наближення контурних струмів обчислена у методі простої ітерації, тобто
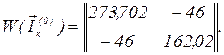
Обчислюємо перше наближення контурних струмів за попередньо наведеним алгоритмом.
Вектор нев’язок

 Обчислюємо вектор
Обчислюємо вектор

Обчислюємо вектор

Параметр ітерації
 Перше наближення вектора контурних струмів
Перше наближення вектора контурних струмів

Обчислюємо евклідову норму

Використовуючи систему символьної математики МаthCad в ітераційному циклі обчислюємо контурні струми з точністю  кількість ітерацій
кількість ітерацій 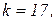 контурні струми
контурні струми 
Метод Ньютона-Рафсона.
Робоча формула Ньютона-Рафсона
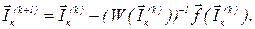
Обчислення першого наближення контурних струмів збігається з методом простої ітерації і відповідно 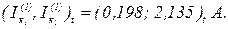
Друге наближення.
Обчислюємо вектор нев’язок
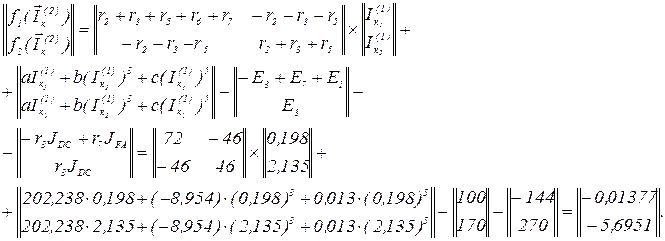 Матриця Якобі
Матриця Якобі



Перевірка точності  , тобто
, тобто

Використовуючи систему символьної математики МаthCad в ітераційному циклі обчислюємо контурні струми з точністю  кількість ітерацій
кількість ітерацій  контурні струми
контурні струми 
Струми віток обчислюємо так

План роботи
1. Ознайомитися з теоретичними відомостями до лабораторної роботи.
2. Вибрати завдання згідно вказаного викладачем варіанту.
3. Намалювати граф електричного кола.
4. Сформувати математичну модель у методі контурних струмів.
6. Використовуючи систему символьної математики МаthCad обчислити контурні струми та струми віток.
6. висновки.
Оформлення звіту
У звіті необхідно навести:
– мету та план роботи;
– короткі теоретичні відомості;
– схему електричного кола та граф схеми;
– матриці, що описують граф електричного кола, параметри та координати електричного кола;
– математичну модель у методі контурних струмів;
– результати розрахунку;
– висновки.
8. Контрольні запитання
1. Як звести систему скінченних нелінійних рівнянь до явної форми?
2. Запишіть рекурентну формулу розв’язання системи скінченних нелінійних рівнянь методом простої ітерації.
3. За якими умовами оцінюється збіжність розв’язання системи скінчених нелінійних рівнянь методом простої ітерації?
4. За яким алгоритмом розв’язується система скінченних нелінійних рівнянь методом ітерації Зайделя?
5. За якими умовами оцінюється збіжність розв’язання системи скінченних нелінійних рівнянь методом ітерації Зайделя?
6. Запишіть рекурентну формулу методу найшвидшого спуску розв’язання системи скінченних нелінійних рівнянь.
7. За яким алгоритмом обчислюють корені системи скінченних нелінійних рівнянь методом найшвидшого спуску?
8. Які підходи використовують для зведення до явної форми системи скінченних нелінійних рівнянь для розв’язання її методом Ньютона-Рафсона?
9. Запишіть рекурентну формулу методу Ньютона-Рафсона розв’язання системи скінченних нелінійних рівнянь.
Список літератури
1. Кириленко О.В., Сегеда М.С., Буткевич О.Ф., Мазур Т.А. Математичне моделювання в електроенергетиці: Підручник / – Львів: Вид-во нац. ун-ту «Львівська політехніка», 2010. – 608 с.
2. Кириленко О.В., Сегеда М.С., Буткевич О.Ф., Мазур Т.А. Математичне моделювання в електроенергетиці: Підручник / 2-е вид. – Львів: Видавництво Львівської політехніки, 2013. – 608 с.
3. Перхач В.С. Математичні задачі електроенергетики – 3-е вид., перероб. і доп. – Львів: Вища шк., 1989. – 464 с.
4. Сегеда М.С. Математичне моделювання в електроенергетиці: Навч. посібник / Мін. освіти і науки України; Національний університет “Львівська політехніка” – Львів: Видавництво Національного університету “Львівська політехніка”, 2002. – 300 с.
5. Чуа Л.О., Пен-Мин Лин. Машинный анализ электрических схем (алгоритмы и вычислительные методы). – М.: "Энергия", 1980. – 640 с.
Завдання
Варіанти схем електричних кіл
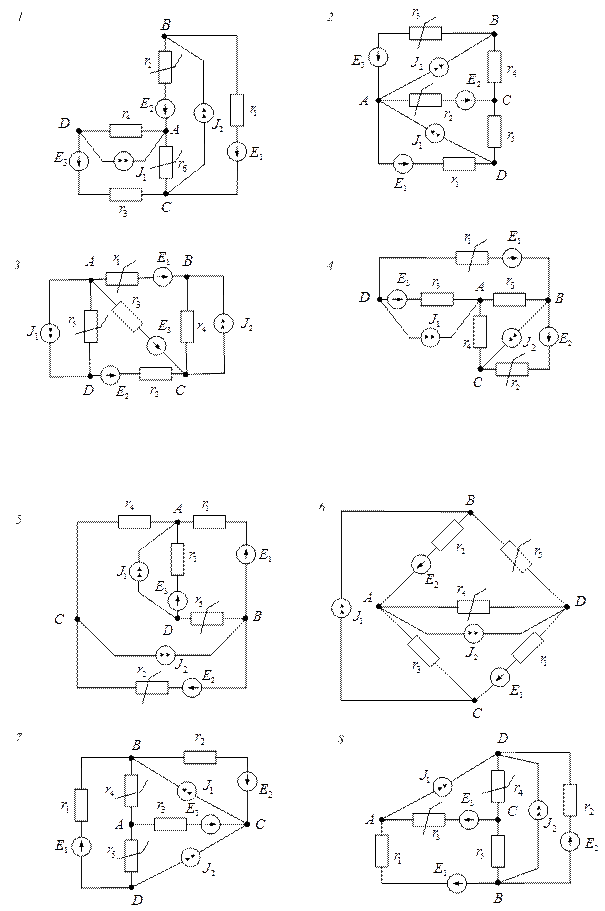
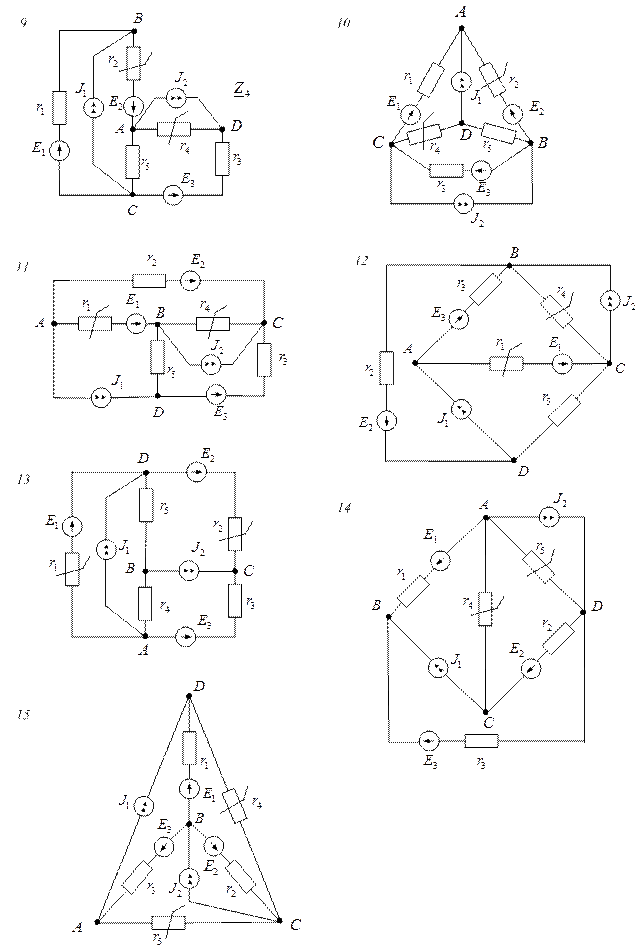

Вихідні дані до завдань
| № Вар. | № схеми | 
| 
| 
| 
| 
| 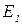
| 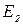
| 
| 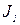
| 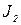
|
| Ом | В | А | |||||||||
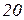
| - | 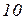
| 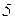
| - | 
| 
| 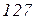
| 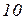
| 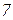
| ||
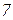
| - | - | 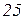
| 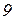
| 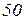
| 
| 
| 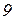
| 
| ||
| - | 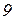
| 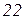
| 
| - | 
| 
| 
| 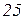
| 
| ||
| - | - | 
| 
| 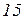
| 
| 
| 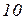
| 
| 
| ||
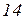
| - | 
| 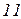
| - | 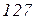
| 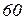
| 
| 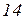
| 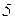
| ||

| 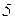
| 
| - | - | 
| 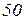
| 
| 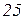
| 
| ||
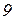
| 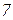
| 
| - | - | 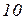
| 
| 
| 
| 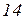
| ||

| 
| - | - | 
| 
| 
| 
| 
| 
| ||

| - | 
| - | 
| 
| 
| 
| 
| 
| ||

| - | 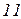
| - | 
| 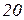
| 
| 
| 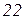
| 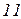
| ||
| - | 
| 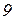
| - | 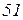
| 
| 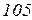
| 
| 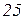
| 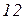
| ||
| - | 
| 
| - | 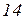
| 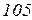
| 
| 
| 
| 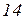
| ||
| - | - | 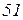
| 
| 
| 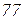
| 
| 
| 
| 
| ||

| 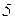
| 
| - | - | 
| 
| 
| 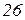
| 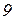
| ||

| 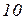
| 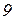
| - | - | 
| 
| 
| 
| 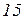
| ||
| - | - | 
| 
| 
| 
| 
| 
| 
| 
| ||

| - | 
| - | 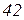
| 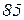
| 
| 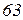
| 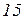
| 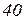
| ||

| 
| 
| - | - | 
| 
| 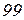
| 
| 
| ||

| - | 
| 
| - | 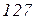
| 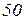
| 
| 
| 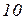
| ||
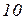
| - | - | 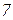
| 
| 
| 
| 
| 
| 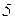
|
Вольт-амперна характеристика нелінійних резисторів

ЗМІСТ
1. Короткі теоретичні відомості………………………………………….3
2. приклад розрахунку…………………………………………………....3
3. План роботи…………………………………………………………….20
4. Оформлення звіту………………………………………………………21
5. Контрольні запитання………………………………………………….21
Список літератури………………………………………………………...22
Завдання……………………………………………………………………23
НАВЧАЛЬНЕ ВИДАННЯ






