Система SmartMath и ее возможности
Назначение системы SmartMath
Начиная с версии 4. 0 система MathCAD обзавелась новым средством оптимизации вычислений — SmartMath. Это фактически экспертная система, ускоряющая вычисления в тех случаях, когда это возможно. При запущенной системе SmartMath процессор численных операций, приступая к вычислению формульного блока, запрашивает символьный процессор о том, может ли тот произвести упрощение или иное преобразование исходной формулы. Если это возможно, то вычисления производятся уже по упрощенной формуле.
Помимо оптимизации вычислений второе важное назначение системы SmartMath заключается в визуализации символьных вычислений и преобразований. Тут дело в том, что символьные вычисления, выполняемые из позиции главного меню Symbolics не наглядны: результат их помещается рядом или под исходным выражением либо замещает его. Откуда он взялся и что именно делается для получения этого результата, в данном случае неясно. К примеру, при вычислении производной некоторого выражения из результата не видно, что вычисляется именно производная, и непонятно, какого она порядка.
Хотя при выполнении символьных операций можно задать опцию вывода комментариев, лишь с применением системы SmartMath процесс символьных преобразований стал очевидным даже в том случае, когда он имеет несколько стадий и выполняется с рядом специальных указаний — директив, которые при этом отображаются в документе.
Система SmartMath более полно использует ядро символьных операций, чем символьные вычисления из подменю позиции Symbolics главного меню, и снимает некоторые ограничения на их выполнение. Например, возможно использование в преобразуемых выражениях функций пользователя. Еще важнее то, что результаты символьных преобразований, выполняемых системой SmartMath, автоматически меняются при изменении исходных символьных данных. Этого, увы, не происходит при символьных вычислениях с помощью команд в позиции Symbolics главного меню.
Описание системы SmartMath не случайно включено в эту главу вместе с разделами по программированию. Она в сущности и является частью программных средств MathCAD, реализующих линейные программы символьных вычислений. При этом блоки символьных вычислений по своей конструкции и идеология их построения очень напоминают программные блоки.
Оператор символьного вывода
Вначале для визуализации результатов символьных преобразований был введен специальный символ — удлиненная горизонтальная стрелка —>. Ее можно вызвать нажатием клавиш Ctrl+. (точка) или вызовом из палитр математических символов (для ввода отношений и символьных операций). Шаблон этого знака имеет вид • —>, где на месте черного прямоугольника вводится подвергаемое символьному преобразованию исходное выражение.
Указанный символ можно рассматривать как простой оператор символьного вывода. Если задать исходное выражение и вывести курсор из формуль-ного блока с ним, то система помещает результат его символьных преобразований после стрелки (оператора символьного вывода). Это и есть первый этап работы с системой SmartMath.
Оператор расширенного символьного вывода
В версию системы MathCAD 7. 0 PRO введен еще один расширенный оператор символьного вывода. Он задается нажатием клавиш Ctrl+ Shift+. (точка) или выбором из палитры символьных операций. Этот оператор имеет вид • • —>. В первый шаблон-прямоугольник вводится исходное выражение, а во второй — директивы символьных преобразований. Они будут описаны чуть позже; задаются эти директивы или вводом соответствующих ключевых слов, или из палитры символьных операций.
Кроме того, в один такой оператор можно ввести другой, с тем чтобы получить составной расширенный оператор символьного вывода и место для записи нескольких директив. Это позволяет намечать заданный путь символьных преобразований. На рис. 12. 1 приведены простейшие примеры применения символьных операций без использования системы SmarthMath и с ее использованием.
Несмотря на простоту примеров, приведенных на рис. 12. 1, они дают наглядное представление об отличительных особенностях реализации символьных операций с помощью операторов символьного вывода, которые были указаны выше.
12. 2. Директивы системы SmartMath и их применение
Состав директив
При вводе стрелки —> после выражения фактически (по умолчанию) над ним исполняется операция Simplify (Упростить). Но что подразумевается под этим, ясно далеко не всегда, даже несмотря на то, что многие символьные операции система выполняет вполне очевидно, например вычисление интеграла или производной в символьном виде.

Рис. 12. 1 Простейшие примеры применения символьных операций
При необходимости выполняемую операцию можно изменить с помощью ряда ключевых слов:
simplify — упрощение выражений;
expand — разложение выражения по степеням;
factor — разложение выражения на простые дроби;
complex — преобразования в комплексной форме;
assume — присваивание переменным неопределенного значения, даже если до этого им были присвоены значения и заданы ограничения на значения переменных;
series — разложение в ряд по заданным переменным;
float — преобразование в формат чисел с плавающей точкой;
literally — запрет символьного преобразования для последующего выражения;
ФBparfac — разложение на элементарные дроби;
Фcoeffs — возвращает коэффициенты полинома;
ФBfourier — прямое преобразование Фурье;
Фlaplace — прямое преобразование Лапласа;
Фztrans — прямое Z-преобразование;
ФBinvfourier — обратное преобразование Фурье;
Фinvlaplace — обратное преобразование Лапласа;
Фinvztrans — обратное Z-преобразование;
ФMT ---> — транспонирование матрицы;
ФМ-1—» — инвертирование матрицы;
Ф¦М¦-> — вычисление детерминанта матрицы;
ФModifier — модифицированные команды:
* assume — вводное слово для приведенных ниже определений;
* real — для var=real означает вещественное значение var;
* RealRange — для var=RealRange(a,b) означает принадлежность вещественной var к интервалу [а,Ь];
» trig — задает направление тригонометрических преобразований.
Ключевые слова допустимо набирать только строчными буквами (кроме Modifier — первая буква в этом слове должна быть прописной). В новой версии MathCAD директивы охватывают все возможные символьные преобразования. При этом их даже больше, чем при использовании операций позиции Symbolics главного меню.
Примеры применения символьных директив
Простейшие примеры на символьные операции даны на рис. 12.2. В этих примерах полезно обратить внимание на множественность применения директив, особенно в примере на применение директивы подстановки substitute.

Рис. 12. 2 Примеры символьных преобразований с помощью системы SmartMath
Как видно из рис. 12. 1 и 12. 2, блоки системы SmartMath имеют следующие отличительные свойства:
дают хорошее визуальное представление операций;
имеют шаблоны для задания параметров и опций;
обеспечивают работу с функциями пользователя;
обеспечивают передачу данных от формулы к формуле;
допускают расширение, позволяющее использовать сразу несколько директив;

Рис. 12.3 Примеры применения символьных вычислений
имеют конструкцию, схожую с конструкцией программных блоков.
На рис. 12. 3 показано еще несколько примеров применения символьных вычислений. Здесь особенно полезно присмотреться к технике применения разложения в ряд Тейлора и преобразования Лапласа.

Рис. 12.4 Примеры на применение директив complex, assume и coeffs

Рис. 12.5 Символьные операции с матрицами
Как нетрудно заметить, директива упрощения simplify не имеет параметров Директива разложения в ряд Тейлора series требует указания двух параметров задания начального значения переменной х и указания числа членов ряда Директивы преобразования Лапласа laplace и решения уравнений solve требуют одного параметра — указания имени переменной (в нашем случае х) С помощью директивы solve можно решать и системы уравнений — тогда ее параметр будет вектором неизвестных.
Применение директив complex, assume и coeffs поясняет рис 12.4. Тут важно обратить внимание на двойственность применения ключевого слова assume Оно может применяться для отмены значений переменных (берется прямо из палитры символьных директив) и для указания статуса и ограничении переменных (берется из дополнительной палитры Modifiers).

Рис. 12.6 Символьное вычисления интегралов
Выполнение матричных операций в символьной форме особой специфики не имеет. На рис. 12.5 показаны основные операции с матрицами, включая их транспонирование и вычисления обратной матрицы и детерминанта матрицы. Для наглядности взята матрица небольшого (2х2) порядка
Рис. 12. 6 показывает применение символьных директив для вычисления интегралов. Здесь, пожалуй, полезно обратить внимание на применение директивы float, позволяющей вычислить значение интеграла в виде обычного вещественного числа
Итак, мы рассмотрели большую часть символьных директив С оставшимися читатель может поработать самостоятельно, тем более что правила их применения уже были описаны
12. 3. Операторы вычисления пределов функций
Для вычисления пределов функций начиная с версии MathCAD PLUS 5 0 в систему введен символьный оператор limit Помимо ввода с наборной панели Calculus Pallete его в трех формах можно ввести нажатием следующих комбинаций клавиш
Ctrl+ L — ввод шаблона оператора вычисления предела функции при х, стремящемся к заданному значению,
Ctrl+ A — ввод шаблона вычисления предела функции слева от заданной точки, Ctrl+ B — ввод шаблона вычисления предела функции справа от заданной точки
На рис. 127 показаны примеры вычисления пределов При вычислении пределов нужно заполнить шаблоны, входящие в главный шаблон для вычисления пределов, а затем ввести функцию, имя переменной, по которой ищется предел, и значение переменной — аргумента функции. Для получения результата установите после блока вычисления предела стрелку с острием, направленным вправо. Предел (если он существует) будет вычислен и появится в шаблоне у острия стрелки. Если функция не имеет предела, вместо результата появится надпись Undefine
12. 4. Задание операторов пользователя
Еще одна экзотическая возможность, присущая новым версиям системы MathCAD, — задание новых операторов пользователя Такой оператор задается практически так же, как функция пользователя, но вместо имени выбирается какой-либо подходящий знак Например, можно задать оператор деления
в виде:

Рис. 12. 7 Примеры вычисления пределов функций
/(А,В):= A/B задание нового оператора деления;
/(6,2) =3 — применение функции деления;
6/2 = 3 — применение нового оператора деления.
При кажущейся простоте такого задания здесь есть проблемы. Встроенные в систему операторы нельзя переопределить. Поэтому набор доступных знаков для обозначения новых операторов ограничен. К примеру, нельзя задать новый оператор деления знаком / (он уже использован), но можно взять знак /поскольку этот символ системой не используется.
Вторая проблема связана с вводом символа нового оператора. Скорее всего, его напрямую ввести нельзя. Придется воспользоваться типовыми приемами ввода новых символов в документы Windows. Один из этих приемов — использование приложения, выдающего таблицу символов, с возможностью его экспорта из этой таблицы в документ другого приложения (в нашем случае — в документ MathCAD).
Можно также воспользоваться подходящим знаком из набора Extra Math Symbol, имеющегося в составе шпаргалок QuickSheet, доступ к которым дает центр ресурсов На рис 12. 8 показан такой вариант задания нового оператора пользователя. Для перетаскивания знака можно скопировать его в буфер об мена с помощью операции Copy, а затем ввести в документ, используя операцию Paste.
После того как оператор задан, его можно использовать как функцию и как оператор. Примеры показаны на рис 12. 8. Для применения нового оператора надо вывести его шаблон с помощью панели математических знаков (она также показана на рис 12 8) В нашем случае следует нажать кнопку xfy этой панели — она выводит особый шаблон вида • • • Введите операнды, например 6 и 2, в крайние прямоугольники, а символ оператора — в средний. Поставив после этой конструкции знак равенства, увидите результат — число 3.
Разумеется, можно задать и другие операторы, например для работы с одним операндом Так, вы можете задать оператор для пересчета значения температуры по шкале Цельсия, с тем чтобы определить соответствующее ему значение по шкале Фаренгейта, следующим образом
°С (х) =9/5 х+32 °F.=1
Затем, используя кнопку xf наборной панели символов отношения, можно выполнять операцию пересчета в виде.
37°С-986 °F
Большинство пользователей MathCAD вправе спросить и зачем только нужны эти сложности? И в самом деле, проще и естественней задать нужную операцию с помощью функции пользователя Однако есть области математики и физики, где задание новых операторов необходимо, поскольку является частью специфического языка их описания Те, кто работает в этих областях, по достоинству оценят предоставляемую возможность, несмотря на определенные неудобства, связанные с назначением новых операторов и их использованием.

Рис. 12. 8 Задание оператора пользователя с выбором имени из набора знаков
12. 5. Задание программных модулей
Программные операторы
Вплоть до появления последних версий системы MathCAD возможности программирования в них были крайне ограниченными. Фактически MathCAD позволяла реализовать лишь линейные программы, в основе которых лежит понятие функции. Функция if и ранжированные переменные в отдельных случаях могли заменить условные выражения и циклы, но с серьезными ограничениями. Отсутствовала возможность задания завершенных программных модулей.
Эти возможности наконец появились в версии MathCAD PLUS 6. 0 PRO и в расширенном варианте имеются в описываемой версии MathCAD 7. 0 PRO. Они сосредоточены в наборной панели программных элементов, показанной на рис. 12. 9.
Как видно из рис. 12. 9, программный модуль в системе MathCAD превратился в самостоятельный модуль, выделяемый в тексте документа жирной вертикальной чертой. Он может вести себя как безымянная функция, не имеющая параметров, но возвращающая результат — первый пример на вычисление квадратного корня из числа 12. Программный модуль может выполнять и роль тела функции пользователя с именем и параметрами — второй пример.
Обзор программных операторов
Нетрудно заметить, что набор программных элементов для создания программных модулей весьма ограничен. Ниже приводится их перечень. Add Line — создает и при необходимости расширяет жирную вертикальную линию, справа от которой в шаблонах задается запись программного блока;
<— — символ локального присваивания (в теле модуля);
if — оператор условного выражения;
for — оператор задания цикла с фиксированным числом повторении;
while — оператор задания цикла типа "пока" (цикл выполняется, пока выполняется некоторое условие);
otherwise — оператор иного выбора (обычно применяется с if);
break — оператор прерывания;
Фcontinue — оператор продолжения;
Фreturn — оператор возврата;
Фоn error — оператор обработки ошибок.
Оператор Add Line
Оператор Add Line выполняет функции расширения программного блока. Расширение фиксируется удлинением вертикальной черты программных блоков или их древовидным расширением. Благодаря этому в принципе можно создавать сколь угодно большие программы.
Оператор <-
Оператор <— выполняет функции внутреннего локального присваивания. Например, выражение х <— 123 присваивает переменной х значение 123. Локальный характер присваивания означает, что такое значение х сохраняет только в теле программы. За пределами тела программы значение переменной х может быть неопределенным либо равным значению, которое задается операторами локального: = и глобального = присваивания вне программного блока.

Рис. 12. 9 Задание программных блоков
Оператор if
Оператор if является оператором условного выражения. Он задается в виде:
Выражение if Условие
Если Условие выполняется, то возвращается значение Выражения. Совместно с этим оператором часто используются оператор прерывания break и оператор иного выбора otherwise.
Оператор for
Оператор for служит для организации циклов с заданным числом повторений. Он записывается в виде:
for Var e Nmin.. Nmax
•
Эта запись означает, что если переменная Var меняется с шагом+ 1 от значения Nmin до значения Nmax, то выражение, помещенное в шаблон, будет выполняться. Переменную счетчика Var можно использовать в выражениях программы.
Оператор while
Оператор while служит для организации циклов, действующих до тех пор, пока выполняется некоторое Условие. Этот оператор записывается в виде:
while Условие
•
Выполняемое выражение записывается на место шаблона.
Оператор otherwise
Оператор иного выбора otherwise обычно используется совместно с оператором if. Это поясняет следующая программная конструкция:
f (x): = 1 if х>0 возвращает 1, если х > О
-1 otherwise возвращает -1 во всех иных случаях
Оператор break
Оператор break вызывает прерывание работы программы всякий раз, когда он встречается. Чаще всего он используется совместно с оператором условного выражения if и операторами циклов while и for, обеспечивая переход в конец тела цикла.
Оператор continue
Оператор continue используется для продолжения работы после прерывания программы. Обычно он применяется совместно с операторами задания циклов while и for, обеспечивая после прерывания возврат в начало цикла.
Оператор return
Оператор return прерывает выполнение программы и возвращает значение своего операнда, стоящего следом за ним. Например, в приведенном ниже случае
return 0 if x<0
будет возвращаться значение 0 при любом х < 0.
Оператор on error
Оператор on error является оператором обработки ошибок, позволяющим создавать конструкции обработчиков ошибок. Этот оператор задается в виде:
Выражение_1 on error Выражение_2
Если при выполнении Выражения_1 возникает ошибка, то выполняется Выражение_2. С оператором on error связана функция error, которая обычно используется для возврата текстового сообщения об ошибке.
12. 6. Примеры программирования
Несмотря на столь скромный набор программных средств, они дают системе MathCAD именно те возможности, которые ранее попросту отсутствовали: задание функций с аппаратом локальных переменных, задание различных видов циклов (в том числе вложенных), упрощение алгоритмов с помощью операций присваивания и реализация по классическим алгоритмам итерационных и рекурсивных процедур. Рекомендуется внимательно изучить рис. 12. 10, на котором показана часть этих возможностей.
Обратите особое внимание на второй пример вычисления факториала. Здесь использовано задание одного программного модуля внутри другого. Вообще говоря, для нескольких подмодулей, которые должны выполняться в составе циклов, надо использовать их объединение в виде жирной вертикальной черты. Для этого, как и для исходного задания блока, служит команда Add Line, добавляющая в модуль дополнительную вертикальную черту для подмодуля.

Рис. 12. 10 Примеры задания программных блоков
Программный модуль в сущности является функцией, но описанной с применением упомянутых сугубо программных средств. Эта функция может возвращать значение, определяемое последним оператором. Это значит, что после такого модуля, выделенного как целый блок, можно поставить знак равенства для вывода значения функции. В блоке могут содержаться любые операторы и функции входного языка системы. Для передачи в блок значений переменных можно использовать переменные документа, которые ведут себя в блоке как глобальные переменные.
Обычно модулю присваивается имя со списком переменных, после которого идет знак присваивания: =. Переменные в списке являются локальными, и им можно присваивать значения при вызове функции, заданной модулем Локальный характер таких переменных позволяет присваивать им те же имена, что и глобальным переменным документа. Однако лучше этого не делать и использовать разные имена для локальных переменных программных модулей и переменных документа.
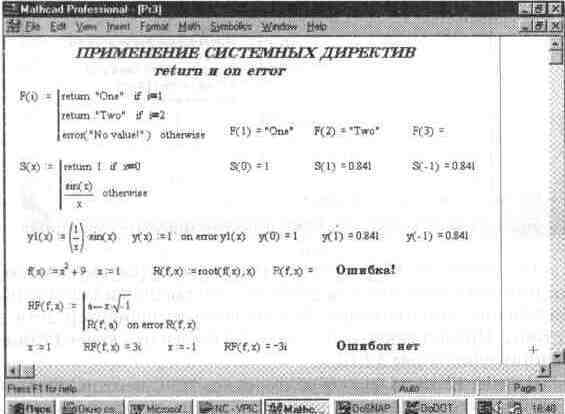
Рис. 12. 11 Применение директив on error и return
На рис. 12. 11 показано применение операторов on error и return, а также действие функции error, задающей вывод надписи в желтом прямоугольнике при активизации мышью выражения, содержащего ошибку.
В этих примерах надо обратить внимание на два момента. Первый — возможность применения оператора on error вне программного блока для задания функции y (x) =sin (x)/x с исключительным значением 1 при х=0. Второй — применение этого оператора для решения уравнения, имеющего комплексные корни. Когда при таком решении задается действительное начальное приближение для х, то функция root (f, x) дает ошибку. Она исправляется с помощью оператора on error при задании функции RF (f, x), имеющей обработчик ошибок.
Задание программных модулей позволяет реализовать любые специальные приемы программирования и может служить мощным средством расширения системы путем задания новых функций.
Теперь рассмотрим достаточно сложный и поучительный пример применения программного блока. На рис. 12. 12 показан документ, в котором программный модуль вычисляет коэффициенты Фурье для заданной функции — пилообразного импульса (его можно менять).
Тут вычисление коэффициентов ряда Фурье выполнено по их классическим интегральным представлениям. Это хорошо иллюстрирует возможность применения в программных блоках весьма мощных средств входного языка системы. Продолжение этого документа, реализующее гармонический синтез, представлено на рис. 12. 13.
На рис. 12. 13 показаны векторы коэффициентов, приведена формула гармонического синтеза исходной функции по ее гармоническому ряду и на графике проведено сопоставление исходной функции с ее представлением рядом Фурье с ограниченным числом гармоник N.
Еще один пример применения программного модуля для задания точек некоторой функции в трехмерном пространстве показан на рис 12 14 Там же представлено построение этих точек внутри параллелепипеда
Разумеется, подобные задачи могут в системе MathCAD решаться и без использования в явном виде программных средств Однако эти средства облегчают решение сложных задач, особенно когда имеется описание их программной реализации на каком-либо языке программирования Тогда несложно перевести реализацию решения задачи с этого языка на язык программирования системы MathCAD.
Вообще, надо отметить, что проблема включения в документы программных блоков в MathCAD решена изящно и красиво, такие блоки подчас просто украшают документы и позволяют пользоваться всеми средствами не только математически ориентированного входного языка MathCAD, но и классического программирования.
Много интересного и поучительного можно найти в примерах задания и применения программных модулей раздела QuickSheet (Шпаргалки), доступного из центра ресурсов системы. Нельзя не отметить, что характер задания программных модулей в MathCAD весьма удачен: модули прекрасно вписываются в документы, выглядят просто и естественно.

Рис. 12. 12 Вычисление коэффициентов А и В разложения функции в ряд Фурье

Рис. 12. 13 Реализация гармонического синтеза
Следует также отметить, что система MathCAD PLUS 7. 0 допускает расширение путем включения в нее новых функций, написанных на языке Си или Си++. Впрочем, возможности системы настолько широки, что трудно себе представить необходимость в таком кардинальном шаге. Это расширение скорее может оказаться полезным для разработчиков системы, чем для подавляющего большинства ее пользователей.
Интересующиеся этой возможностью могут воспользоваться описанием ее в [14].

Рис. 12. 14 Применение программного модуля для построения точек заданной функции в пространстве
12. 7. Погрешности вычислений и сообщения об ошибках

Рис. 12. 15 Влияние переменной TOL на погрешности вычисления производных и интегралов
Большинство вычислений в системе реализовано с помощью численных методов, принципиально имеющих конечную погрешность вычислений. Так, для вычислений производной используется конечно-разностный метод с изменением шага между узлами и его подстройкой под заданную погрешность. Интегралы вычисляются методом Симпсона с заданной погрешностью, а для вычисления корней функций применяется метод секущих.
Для всех методов погрешность вычислений задается с помощью специальной системной переменной TOL. Хотя истинная погрешность может оказаться значительно меньше значения TOL, ее влияние на результаты вычислений все же заметно (см. рис. 12. 15).
При выполнении вычислений возможны ошибки. Система выводит сообщения об ошибках, закрашивая ошибочные имена идентификаторов в ярко-красный цвет. В прежних версиях MathCAD сообщения об ошибках появлялись в красных прямоугольниках с линией, отходящей от места ошибки к прямоугольнику с сообщением о ней. Однако это загромождало документ, и от такого способа в новой версии отошли. В новой версии MathCAD подробное сообщение об ошибке можно получить также, установив на выражение с ошибкой курсор мыши и нажав ее левую клавишу.
Ниже представлен список основных сообщений об ошибках:
array size mismatch — несоответствие размера массива;
cannot be defined — не может быть определено;
cannot take subscript — не содержит верхних (нижних) индексов, definition stack overflow — переполнение стека определений;
did not find solution — решение не найдено;
dimension to non real power — размерность массива — не целое число;
domain error — ошибка области определения;
duplicate — дублирование;
equation too large — слишком большое выражение;
error in constant — ошибка в константе;
error in list — ошибка в списке;
error in solve block — ошибка в блоке;
file error — ошибка в файле;
file not found — файл не найден;
illegal array operation — неверная операция с массивом;
illegal context — неверный контекст;
illegal factor — неверный множитель;
illegal function name — неверное имя функции;
illegal ORIGIN — неверное употребление ORIGIN;
illegal range — неправильный диапазон;
illegal tolerance — некорректная точность аппроксимации;
incompatible units — несовместимые единицы;
index out of bounds — индекс вне границ;
interrupted — решение прервано;
invalid order — неверный порядок;
list too long — длинный входной список;
misplased comma — неуместная запятая;
missing operand — пропущенный операнд;
missing operator — пропущенный знак операции;
must be 3-vector — должен быть трехмерный вектор;
must be array — должен быть массив;
must be dimensionless — должен быть безразмерным;
must be increasing — должен быть возрастающим;
must be integer — должен быть целым;
must be nonzero — должен быть ненулевым;
must be positive — должен быть положительным;
must be range — должен быть диапазон;
must be real — должен быть вещественным;
must be scalar — должен быть скаляром;
must be vector — должен быть вектором;
nested solve block — следующий блок решения;
no matching Given — нет соответствующего Given;
no scalar value — нескалярная величина;
not a name — не является именем;
not converging — не конвертируется;
only one array allowed — допустим только один массив;
overflow — переполнение;
significance lost — потеряны значащие цифры;
singularity — деление на нуль;
stack overflow — переполнение стека;
subscript too large — слишком большой нижний индекс;
too few arguments — слишком мало аргументов;
too few constraints — слишком мало ограничений;
too few elements — слишком мало элементов;
too few subscripts — мало нижних индексов;
too large to display — слишком велико, чтобы быть отображенным;
too many arguments — слишком много аргументов;
too many constraints — слишком много ограничений;
too many points — слишком много точек;
too many subscripts — слишком много индексов;
undefindet — не определено;
unmatched parenthesis — дисбаланс скобок;
wrong size vector — неверный размер вектора.
Сообщения об ошибках кратки, но их анализ не вызывает особых затруднений. Заметим, что приведенный список содержит далеко не все ошибки, а лишь наиболее распространенные.
12. 8. Реализация численных методов в MathCAD 7. 0 PRO
Серьезные пользователи, работающие с математическими системами, зачастую бывают недовольны отсутствием информации о реализованных в таких системах численных методах. Связано это с тем, что нередко от этих методов зависит успех решения особых задач, с которыми может столкнуться каждый пользователь. Поэтому немного остановимся на сути численных методов, реализованных в системе MathCAD 7. 0 PRO.
Прежде всего отметим, что выражения 0*x, 0/х и 0/0 система вычисляет как 0. Точнее говоря, встречая 0 в числителе любого выражения, она не вычисляет это выражение, а просто полагает его значение равным 0. При реализации численных методов MathCAD дает точными 15 десятичных цифр для результатов вычислений, но при выводе задает число знаков в соответствии с выбранным форматом чисел.
Определенные интегралы система вычисляет методом Ромберга. Этот метод широко описан в нашей литературе (см., например, [1, 2]). Поэтому, не описывая его подробно, отметим лишь, что он является вариантом метода трапеций с делением на два интервала интегрирования с итерационным уточнением решения до достижения заданной точности (она определяется значением системной переменной TOL).
Если за заданное число итераций точность не достигнута, используется более точный метод Ромберга с открытыми концами. При нем число интервалов утраивается на каждом шаге интегрирования. Этот метод увеличивает число шагов интегрирования там, где подынтегральная функция меняется более резко (например, если она имеет разрыв).
К достоинствам метода можно отнести то, что он делает все возможное, чтобы вычислить интеграл даже при сложной функции. Но для простых функций это ведет к увеличению времени вычислений. При наличии у подынтегральной функции особенностей время вычисления может резко возрастать из-за перехода от одной реализации метода Ромберга к другой. Поэтому нередко бывает оправданным применение достаточно точных формул интегрирования, например формул Ньютона — Котесса с легко предсказуемыми узлами, которые можно выбрать вдали от особых точек подынтегральной функции. Примеры такого подхода даны в Главе 14.
Для вычисления производных порядка от 0 до 5 система использует метод Риддера. Подробности о нем можно найти в [14]. Главное то, что метод вычисляет первую производную с погрешностью до 7—8 верных цифр результата, а с повышением производной на порядок число верных цифр уменьшается на единицу. Метод Риддера — итерационный (на каждой итерации шаг дифференцирования уменьшается), но число итераций ограничено. Если при реализации этого метода указанная точность не достигается, MathCAD сообщает об отсутствии сходимости.
При решении систем уравнений и неравенств используется итерационный метод Левенберга — Маркардта, содержащийся в известном и свободно распространяемом пакете алгоритмов численных методов MINPACK. Этот метод пытается найти нули или минимум среднеквадратичной погрешности при решении заданной системы уравнений или системы неравенств. При решении с применением аппарата комплексных чисел раздельно решаются действительная и мнимая части уравнений.
При решении вычисляется также вектор невязки. Если его величина меньше TOL, система возвращает вектор переменных-неизвестных. Если для решения используется функция find, при величине вектора невязки больше TOL система сообщает, что решение не найдено. Когда используется функция minerr, вектор неизвестных возвращается даже в том случае, когда значение вектора невязки больше TOL. Наконец, если не обнаружено схождение за заданное число итераций, выдается сообщение об отсутствии сходимости (как при применении функции find, так и minerr). В любых случаях величина вектора невязки определяется значением переменной ERR.
Для вычисления определителей матрицы и ее инвертирования используется LU-разложение. При этом матрица М разлагается в произведение нижней треугольной матрицы L и верхней U (т. е. M=L-U). Такой метод хорошо известен. В частности, он позволяет:
• вычислить определитель исходной матрицы как произведение диагональных элементов матриц L и U;
• вычислить обратную матрицу из решения матричного уравнения M*Vj=ej, где е — вектор с единицей на j-м месте и нулями в остальных позициях, V— вектор решения, который образует столбцы обратной матрицы для каждогоj;






