Модуль 2. векторы. комлексные числа. кривые
Лекция 4. Векторы, линейные операции над ними. скалярное произведение векторов
1. Геометрические векторы
2. Действия над векторами
3. Система координат.
4. Координаты вектора. Преобразования координат вектора при основных операциях.
5. Модуль вектора. Расстояние между двумя точками.
6. Скалярное произведение векторов.
Установление связи между алгеброй и геометрией было, по существу, революцией в математике. Это позволило воспринимать математику как единую науку и способствовало ее быстрому развитию. Рене Декарт (1637) дал описание метода координат, а развитие его идей привело к развитию ветви математики – аналитической геометрии.
Геометрические векторы
Есть величины, которые полностью определяются заданием своих числовых значений. Например, масса, длина, площадь, объем. Это скалярные величины. Но есть величины, для задания которых необходимо знать еще и направление. Например, сила, скорость, ускорение. Это векторные величины.
· Вектором  называется направленный отрезок:
называется направленный отрезок:  – начало вектора,
– начало вектора,  – конец вектора. Также вектор будем обозначать
– конец вектора. Также вектор будем обозначать 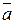 ,
,  ,
,  - латинскими буквами со стрелками.
- латинскими буквами со стрелками.
· Модулем вектора (длиной) называется расстояние между началом и концом. Обозначается  .
.
· Векторы  и
и 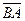 называются противоположными.
называются противоположными.
· Вектор, для которого начало и конец которого совпадают, называется нулевым вектором 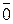 .
.
· Векторы называются коллинеарными, если они расположены на одной прямой или на параллельных прямых.




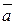
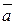 ||
|| 
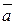 ||
|| 
Коллинеарные векторы
· Векторы называются равными, если они коллинеарные, одинаково направлены и равны по длине.
Пример 1. Построим векторы, образующие ромб  . Укажем равныевекторы
. Укажем равныевекторы  . Отметим неравные векторы
. Отметим неравные векторы  .
.

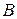



·  Векторы называются компланарными, если они находятся в одной плоскости или на параллельных плоскостях.
Векторы называются компланарными, если они находятся в одной плоскости или на параллельных плоскостях.

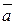

Компланарные векторы  ,
,  ,
, 
Операции над векторами
Операции умножение вектора на число  и сложение векторов
и сложение векторов 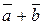 называются линейными операциями над векторами.
называются линейными операциями над векторами.
1. Умножение вектора 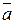 на число
на число  . Если
. Если  , то нужно отложить от начальной точки вектора
, то нужно отложить от начальной точки вектора 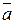 в направлении вектора
в направлении вектора 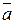 вектор длины
вектор длины  . Если
. Если 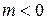 , то нужно отложить от начальной точки вектора
, то нужно отложить от начальной точки вектора 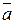 в направлении, противоположном вектору
в направлении, противоположном вектору 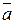 , вектор длины
, вектор длины  .
.
 Пример 2. Рассмотрим вектор
Пример 2. Рассмотрим вектор  и число
и число  . Построим
. Построим  .
.
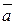

Сложение векторов.
Векторы можно складывать по правилам треугольника и параллелограмма.
По правилу треугольника суммой векторов 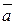 и
и  является вектор
является вектор  , начало которого совпадает с началом вектора
, начало которого совпадает с началом вектора  , а конец – с концом вектора
, а конец – с концом вектора  , при условии, что начало
, при условии, что начало  приложено к концу
приложено к концу  .
.

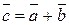 Правило треугольника
Правило треугольника


По правилу параллелограмма суммой векторов  и
и  , имеющих общее начало, называется вектор
, имеющих общее начало, называется вектор  , который выходит из общей точки векторов
, который выходит из общей точки векторов  и
и  и является диагональю параллелограмма, построенного на векторах
и является диагональю параллелограмма, построенного на векторах  ,
,  .
.



Правило параллелограмма

Если имеется несколько векторов  , то сложить их можно следующим образом:
, то сложить их можно следующим образом:





Правило многоугольника

 3. Разностью векторов
3. Разностью векторов 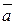 и
и  называется вектор, равный сумме векторов
называется вектор, равный сумме векторов 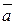 и
и  , т.е.
, т.е.  .
.

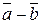

Множество геометрических векторов на прямой обозначается 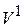 , на плоскости -
, на плоскости -  , в пространстве -
, в пространстве - 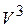 .
.
Система координат
Аналитическая геометрия изучает свойства геометрических фигур (линий, поверхностей) средствами алгебры (с использованием чисел и алгебраических операций) на основе метода координат. Данный метод позволяет каждой точке на плоскости поставить в соответствие упорядоченную пару чисел, а каждой точке пространства – упорядоченную тройку чисел. Основным инструментом метода координат служит система координат.
Далее будем рассматривать только прямоугольную, или декартову, систему координат.
В школьном курсе было дано определение метода координат.
· Осью координат называется прямая линия, на которой зафиксирована точка О (называемая началом координат), выбраны положительное направление (указывается стрелкой) и единица длины.
Каждому действительному числу  соответствует точка
соответствует точка 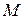 на оси координат, это число называется координатой точки на оси координат, что записывается как
на оси координат, это число называется координатой точки на оси координат, что записывается как  . И обратно: каждой точке
. И обратно: каждой точке 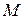 оси координат соответствует действительное число. Это соответствие взаимно однозначное:
оси координат соответствует действительное число. Это соответствие взаимно однозначное:  .
.

 (ось ординат)
(ось ординат)  (ось аппликат)
(ось аппликат)





О 
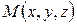

 (ось абсцисс)
(ось абсцисс)


 (ось ординат)
(ось ординат)

 (ось абсцисс)
(ось абсцисс)
Системы координат
· Прямоугольной системой координат на плоскости называется совокупность двух взаимно перпендикулярных осей координат, имеющих общее начало.
Каждой упорядоченной паре чисел  соответствует единственная точка на плоскости
соответствует единственная точка на плоскости 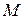 , и обратно:
, и обратно: 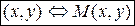 .
.
Числа  и
и  называются координатами точки
называются координатами точки 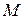 в системе координат OXY. Число
в системе координат OXY. Число  называется абсциссойточки и является координатой основания перпендикуляра, опущенного из точки
называется абсциссойточки и является координатой основания перпендикуляра, опущенного из точки 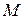 на горизонтальную ось (ось абсцисс). Число
на горизонтальную ось (ось абсцисс). Число  называется ординатойточки и является координатой основания перпендикуляра, опущенного из точки
называется ординатойточки и является координатой основания перпендикуляра, опущенного из точки 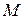 на вертикальную ось (ось ординат).
на вертикальную ось (ось ординат).
· Прямоугольной системой координат в пространстве называется совокупность трех взаимно перпендикулярных осей координат, имеющих общее начало.
Оси ОХ, ОУ и ОZ называются осями абсцисс, ординат и аппликат.
Каждой точке 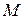 пространства соответствует упорядоченная тройка чисел
пространства соответствует упорядоченная тройка чисел  , которые называются координатами точки в системе координат OXYZ. Это соответствие взаимно однозначное:
, которые называются координатами точки в системе координат OXYZ. Это соответствие взаимно однозначное:
 .
.
Итак, положение точки на прямой относительно оси координат определяется заданием одного числа;
положение точки на плоскости относительно введенной системы координат - двух упорядоченных чисел;
положение точки в пространстве – упорядоченной тройкой чисел (абсциссой, ординатой, аппликатой), которые называются прямоугольными (декартовыми) координатами точки.
В дальнейшем под словом «точка» часто будем понимать ее координаты.
Важной задачей является нахождение расстояния между двумя точками:
1) расстояние между точками  и
и  на прямой равно модулю разности их координат:
на прямой равно модулю разности их координат:
 ;
;
2) расстояние между двумя точками  и
и  на плоскости вычисляется по формуле
на плоскости вычисляется по формуле
 ;
;
3) расстояние между двумя точками  и
и  в пространстве вычисляется по формуле
в пространстве вычисляется по формуле
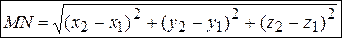 .
.
Координаты вектора. Преобразования координат вектора при основных операциях
Дан вектор  в пространстве. Известны координаты точек
в пространстве. Известны координаты точек  и
и  . Тогда координаты вектора
. Тогда координаты вектора  вычисляются по правилу: из координат конечной точки нужно вычесть координаты начальной точки:
вычисляются по правилу: из координат конечной точки нужно вычесть координаты начальной точки:  .
.
При умножении вектора  на число
на число  его координаты умножаются на это число:
его координаты умножаются на это число:  .
.
При сложении векторов  и
и  складываются соответствующие координаты:
складываются соответствующие координаты:  .
.
Пример 3. На плоскости  даны точки
даны точки  ,
,  ,
,  . Найдите координаты векторов
. Найдите координаты векторов  ,
, 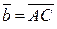 ,
, 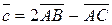 .
.
 ;
;
 ;
;
 .
.






