Обработка результатов измерений. Цель работы – Исследование характера поляризации лазерного излучения и экспериментальная проверка законов Малюса и Брюстера.

ПОЛЯРИЗАЦИЯ СВЕТА. ЗАКОНЫ МАЛЮСА И БРЮСТЕРА

 

 

Работу выполнил:

Студент 2 курса

Группы P3251

Бессонов А.М.

 

Санкт-Петербург

2016 г.

ПОЛЯРИЗАЦИЯ СВЕТА. ЗАКОНЫ МАЛЮСА И БРЮСТЕРА

Цель работы – Исследование характера поляризации лазерного излучения и экспериментальная проверка законов Малюса и Брюстера.

Требуемое оборудование

Модульный учебный комплекс МУК-ОВ.

Краткое теоретическое введение

Поперечные волны обладают особым, присущим только им, свойством, известным под названием поляризация. Под этим понимается пространственное соотношение между направлением распространения светового луча и направлением колебания вектора напряженности электрического (или магнитного ) поля. Теория Максвелла для электромагнитной волны утверждает только, что векторы напряженности электрического и магнитного полей лежат в плоскости, перпендикулярной направлению распространения света, но не накладывает никаких ограничений на их поведение в этой плоскости. Друг относительно друга вектора и ориентированы взаимно перпендикулярно. Поэтому для описания колебаний в световой волне достаточно указывать один из них. Исторически таким вектором выбран вектор напряженности электрического поля , который также называют световым.

Если при распространении световой волны направление колебаний электрического вектора бессистемно, хаотически изменяется с равной амплитудой и, следовательно, любое его направление в плоскости, перпендикулярной распространению волны, равновероятно, то такой свет называют неполяризованным, или естественным. Если колебания электрического вектора фиксированы строго в одном направлении, свет называется линейно- или плоско-поляризованным. В этом случае плоскость, образованная направлением распространения электромагнитной волны и направлением колебаний вектора напряженности электрического поля, называется плоскостью поляризации электромагнитной волны.

Если конец электрического вектора описывает эллипс или окружность, поляризация будет соответственно эллиптической или круговой (циркулярной).

Для анализа поляризации света применяются устройства, называемые поляризаторами. С технической стороны поляризаторы могут быть самых разных типов: кристаллические, пленочные, отражательные и т. п. Но независимо от конкретного устройства, поляризатор пропускает свет с определенной ориентацией вектора . Таким образом, прошедший через поляризатор свет всегда линейно поляризован.

Широкое распространение для получения плоско-поляризованного света имеют поляризаторы, действие которых основано на явлении дихроизма – селективного поглощения света в зависимости от направления колебаний электрического вектора световой волны. Сильным дихроизмом обладают кристаллы турмалина. В данной работе для получения плоско-поляризованного света применяются поляроиды – пленки на которые нанесены кристаллики герапатита – двоякопреломляющего вещества с сильно выраженным дихроизмом в видимой области.

Поляризаторы можно использовать и в качестве анализаторов – для определения характера и степени поляризации интересующего нас света. Пусть на анализатор падает линейно-поляризованный свет, вектор которого составляет угол с плоскостью пропускания P (рис. 3, где направление светового пучка перпендикулярно к плоскости рисунка). Анализатор пропускает только ту составляющую вектора , которая параллельна его плоскости пропускания P, т. е.
Интенсивность пропорциональна квадрату модуля светового вектора (), поэтому интенсивность прошедшего света:

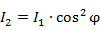, (1)

где — интенсивность падающего плоско-поляризованного света. Это соотношение было установлено в 1810 г. французским физиком Этьеном Луи Малюсом и носит название закона Малюса.

Одной из количественных характеристик поляризации является степень поляризации P. Для ее определения измеряется интенсивность прошедшего света при вращении поляризатора вокруг направления светового пучка. Определяются максимальная I _max и минимальная I _min интенсивности (соответствующие двум ортогональным ориентациям поляризатора) и вычисляется величина P по формуле

. (2)

Поляризация света наблюдается при отражении и преломлении света на границе прозрачных изотропных диэлектриков. Если угол падения естественного света на границу раздела двух прозрачных диэлектриков отличен от нуля, то отраженный и преломленный пучки оказываются частично-поляризованными (рис. 1). В отраженном свете преобладают колебания вектора , перпендикулярные к плоскости падения, а в преломленном свете – параллельные плоскости падения. Степень поляризации обеих волн (отраженной и преломленной) зависит от угла падения. Соответствующую зависимость в 1815 г. установил шотландец Дэвид Брюстер. Как показали опыты, отраженный луч оказывается полностью поляризованым (колебания вектора в нем перпендикулярны плоскости падения) в случае, когда угол между отраженным и преломленным лучом равен 90°. Прошедший луч поляризован частично и содержит преимущественно параллельную составляющую вектора .

Объяснение эффекту Брюстера дал в 1823 г. один из создателей волновой теории света французский физик Огюст Френель. Он доказал, что коэффициенты отражения для света, поляризованного параллельно и перпендикулярно плоскости падения, равны

(3)

Значение угла, соответствующего полной поляризации отраженного луча, определяется из закона преломления:

, (4)

т.е.

(5)

Соответствующий угол падения называют углом Брюстера.

Если на границу раздела двух диэлектриков под углом Брюстера падает плоско-поляризованный свет (например, от лазера) с направлением колебаний вектора в плоскости падения волны, то интенсивность отраженной волны становится близкой к нулю. Однако коэффициент отражения при этом равен

, (6)

что для границы раздела воздух–стекло равно примерно 0,15. Поэтому получать таким образом линейно-поляризованный свет энергетически невыгодно.

Степень поляризации преломленной волны при угле падения, равном углу Брюстера, достигает максимального значения, однако эта волна остается лишь частично поляризованной со степенью поляризации

. (7)

Для границы воздух–стекло степень поляризации прошедшего света всего 8%, повысит ее можно путем ряда последовательных отражений и преломлений. Это осуществляют с помощью, так называемой стопы Столетова, состоящей из нескольких одинаковых и параллельных друг другу пластинок, установленных под углом Брюстера к падающему свету. При достаточно большом числе пластинок проходящий через эту систему свет будет практически полностью линейно-поляризованным. Интенсивность прошедшего через такую стопу света (в отсутствие поглощения) будет равна половине падающего на стопу естественного света.

Эта идея нашла высокоэффективное использование в лазерах, где торцы разрядной трубки представляют собой плоскопараллельные стеклянные пластинки, расположенные под углом Брюстера к оси трубки (рис. 2). Поэтому излучение, распространяющееся вдоль оси трубки между зеркалами и поляризованное в плоскости падения на пластинки, многократно проходит сквозь них практически беспрепятственно, не испытывая отражения. В результате из лазера выходит луч, поляризованный в этой плоскости, что и показано на рисунке. Для другой составляющей излучения, плоскость поляризации которой перпендикулярна плоскости падения, из-за отражений коэффициент усиления оказывается меньше единицы и генерация отсутствует. Таким образом, излучение лазера оказывается линейно поляризованным.

Методика эксперимента

При проведении эксперимента необходимо учитывать то, что в анализаторе теряется часть световой энергии. Поэтому закон Малюса будет иметь следующий вид:

, (8)

где — интенсивность света, прошедшего через анализатор, — интенсивность плоско-поляризованного падающего света, — коэффициент пропускания, который можно найти по следующим формулам:

для параллельной ориентации

, (9)

для перпендикулярной ориентации

, (10)

где , — максимальная и минимальная интенсивности прошедшего света, найденная при вращении анализатора.

Упражнение 1. Проверка закона Малюса

Обработка результатов измерений

1.1. Найду максимальное значение интенсивности излучения, прошедшего сквозь поляризатор = 0,977, соответствующее углу = 0. Получу нормированные значения относительной интенсивности . Результаты занесу в таблицу 1.

Таблица 1

j	I	I	I	Iср
	0,649	0,651	0,650	0,650	0,665	0,750
	0,51	0,55	0,53	0,53	0,532	0,587
	0,36	0,42	0,40	0,393	0,394	0,413
	0,216	0,22	0,225	0,22	0,221	0,250
	0,1	0,115	0,117	0,111	0,111	0,117
	0,023	0,028	0,021	0,024	0,024	0,030
	0,007	0,009	0,005	0,007	0,007	0,000
	0,046	0,051	0,042	0,046	0,046	0,030
	0,129	0,133	0,127	0,13	0,13	0,117
	0,258	0,255	0,261	0,258	0,259	0,250
	0,432	0,436	0,437	0,435	0,436	0,413
	0,573	0,577	0,575	0,575	0,577	0,587
	0,764	0,771	0,768	0,768	0,77	0,750
	0,87	0,875	0,877	0,874	0,877	0,883
	0,948	0,951	0,953	0,951	0,954	0,970
	0,974	0,977	0,979	0,977		1,000
	0,879	0,883	0,877	0,88	0,883	0,970
	0,765	0,769	0,761	0,765	0,767	0,883
	0,623	0,626	0,625	0,625	0,627	0,750
	0,46	0,466	0,463	0,463	0,464	0,587
	0,313	0,315	0,311	0,313	0,314	0,413
	0,178	0,181	0,174	0,178	0,179	0,250
	0,07	0,075	0,077	0,074	0,074	0,117
	0,014	0,016	0,018	0,016	0,016	0,030
	0,009	0,014	0,012	0,012	0,012	0,000
	0,051	0,055	0,052	0,053	0,053	0,030
	0,143	0,145	0,147	0,145	0,145	0,117
	0,287	0,288	0,29	0,288	0,289	0,250
	0,45	0,456	0,453	0,453	0,454	0,413
	0,589	0,587	0,591	0,589	0,591	0,587
	0,78	0,783	0,788	0,784	0,786	0,750

 

 

1.2. Построю график зависимости нормированной интенсивности от угла .

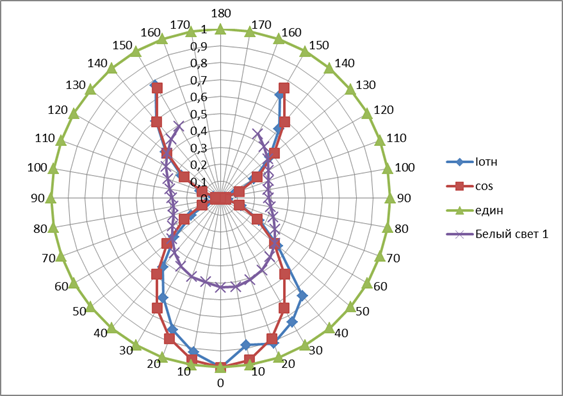
1.3. На той же координатной плоскости построю график зависимости от угла поворота поляроида . Имеем плоскополяризованный свет.

1.4. Найду коэффициенты пропускания использованного поляроида для параллельной и перпендикулярной ориентации его плоскости пропускания по отношению направлению колебаний вектора 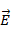в излучении лазера: = 1,197 и = 0,007.

1.5. Найдите степень поляризации излучения белого источника

1.6. На той же координатной плоскости по данным п. 1.8 построю зависимость 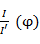для белого света по данным из таблицы 2.

1.7. Таблица 2.

j				()ср
	0,311	0,315	0,316	0,496
	0,27	0,273	0,275	0,431
	0,23	0,235	0,233	0,368
	0,196	0,198	0,199	0,312
	0,17	0,166	0,174	0,269
	0,156	0,151	0,156	0,243
	0,158	0,155	0,156	0,247
	0,167	0,164	0,165	0,261
	0,194	0,194	0,19	0,304
	0,232	0,235	0,236	0,37
	0,267	0,263	0,264	0,418
	0,304	0,306	0,309	0,484
	0,34	0,345	0,346	0,543
	0,366	0,372	0,367	0,582
	0,379	0,383	0,386	0,605
	0,375	0,377	0,384	0,598
	0,366	0,366	0,374	0,582
	0,349	0,352	0,353	0,555
	0,316	0,318	0,319	0,502
	0,275	0,273	0,274	0,433
	0,238	0,239	0,235	0,375
	0,196	0,197	0,192	0,308
	0,168	0,169	0,165	0,264
	0,153	0,154	0,148	0,24
	0,154	0,154	0,154	0,243
	0,17	0,171	0,174	0,271
	0,2	0,206	0,208	0,323
	0,23	0,228	0,235	0,348
	0,274	0,272	0,274	0,432
	0,308	0,304	0,306	0,489
	0,338	0,336	0,339	0,533

Вывод: В ходе выполнения лабораторной работы мы исследовали характер поляризации лазерного излучения, и благодаря графику зависимости нормированной интенсивности от угла поворота поляроида в полярных координатах определили, что поляризация лазера - линейная, были экспериментально проверены законы Малюса(интенсивность света, прошедшего через анализатор, пропорциональна квадрату косинуса угла между плоскостями пропускания поляризатора и анализатора),что видно из графика зависимости от угла поворота поляроида , и Брюстера, степень поляризации света лазера.

Контрольные вопросы

1. Чем отличается линейно-поляризованный свет от естественного?

В естественном свете присутствуют световые колебания всевозможных направлений, каждое из которых перпендикулярно направлению распространения света. В поляризованном свете присутствуют световые колебания только одного направления, совпадающего с оптической осью поляроида.

2. Чем отличается линейно-поляризованный свет от света, поляризованного по кругу?

Линейно-поляризованный свет - свет, в котором вектор (и, следовательно, ) колеблется только в одном направлении, перпендикулярном лучу. Свет, поляризованный по кругу, - свет, для которого вектор (вектор ) изменяется со временем так, что его конец описывает эллипс, лежащий в плоскости, перпендикулярной лучу.

3. Чему равна степень поляризации циркулярно-поляризованного света?

К циркулярно поляризованному свету понятие степени поляризации не применимо, Р=1 всегда.

4. Можно ли имея в распоряжении поляризатор и анализатор определить тип поляризации света (линейная, круговая, эллиптическая).

Можно. Например, поляризаторы можно использовать в качестве анализаторов – для определения характера и степени поляризации интересующего нас света.

5. Как зависит угол Брюстера от показателя преломления первой среды?

где - показатель преломления второй среды относительно первой, - угол падения (угол Брюстера).

Тангенс угла Брюстера обратно пропорционален показателю преломления первой среды.

6. Как зависит угол Брюстера от показателя преломления второй среды?

Тангенс угла Брюстера прямо пропорционален показателю преломления второй среды.

7. Какова связь между углами Брюстера при падении света на границу воздух–стекло со стороны воздуха и со стороны стекла?