Типы векторных объектов, основанные на определении пространственных размеров

Безразмерные типы объектов

· Точка - определяет геометрическое местоположение

· Узел - топологический переход или конечная точка, также может определять местоположение

Одномерные типы объектов

· Линия - одномерный объект

· Линейный сегмент - прямая линия между двумя точками

· Строка - последовательность линейных сегментов

· Дуга - геометрическое место точек, которые формируют кривую определенную математической функцией

· Связь - соединение между двумя узлами

· Направленная связь - связь с одним определенным направлением

· Цепочка - направленная последовательность непересекающихся линейных сегментов или дуг с узлами на их концах

· Кольцо - последовательность непересекающихся цепочек, строк, связей или замкнутых дуг

Двумерные типы объектов

· Область - ограниченный непрерывный объект, который может включать или не включать в себя собственную границу

· Внутренняя область - область, которая не включает собственную границу

· Полигон (контур) - 2-мерный (площадной) объект, внутренняя область, образованная замкнутой последовательностью дуг в векторно-топологических представлениях или сегментов в модели "спагетти". Различают простой П., не содержащий внутренних П., и составной П, содержащий внутренние П., называемые также "островами" (island) и анклавами (hole).

· Пиксель - элемент изображения, который является самым малым неделимым элементом изображения

Пример слоев, составленных из пространственных объектов линейного типа

Примеры слоев, составленных из пространственных объектов полигонального типа

Топологическое представление векторных объектов

Формирование топологии включает определение и кодирование взаимосвязей между точечными, линейными и площадными объектами.

Сопоставление растровой и векторной моделей данных

Преимущества

Растровая модель	Векторная модель
1. Простая структура данных 2. Эффективные оверлейные операции 3. Работа со сложными структурами 4. Работа со снимками	1. Компактная структура 2. Топология 3. Качественная графика

 

 

Квадротомическое дерево (квадродерево) - структура данных, используемая для представления двумерных пространственных данных. Существует несколько типов квадродеревьев в зависимости от базового типа данных. (точки, площади, кривые, поверхности или объемы). Наиболее общим типом квадродерева и примером использования является квадродерево растрового изображения (см. рисунок 1, рисунок 3 и рисунок 4 - примеры изображения и его бинарного представления, блоков разбиения и квадродерева). Далее, для конкретности, под пространственными данными везде будем понимать растровое изображение.

Следуя Samet (1990), под двумерным изображением понимается массив элементов изображения (пикселов, pixel). Если каждый из пикселов имеет только два состояния - черный или белый (подсвечен или нет), то изображение называется бинарным. Если пикселы могут принимать более двух значений, то их значения могут трактоваться как оттенки серого, а изображение в этом случае называется изображением в градациях серого (grey-scale). Цветные изображения организованы аналогичным образом. Квадродеревья наиболее широко используются для работы с двухцветными изображениями, поэтому в дальнейшем будем иметь дело преимущественно с бинарными изображениями. Будем также в дальнейшем подразумевать, что фоновым в бинарном изображении является белый цвет.

При построении квадродерева двумерное изображение рекурсивно подразделяется на квадранты. Каждый из четырех квадрантов становится узлом квадротомического дерева. Больший квадрант становится узлом более высокого иерархического уровня квадродерева, а меньшие квадранты появляются на более низких уровнях. Преимущества такой структуры в том, что регулярное разделение обеспечивает простое и эффективное накопление, восстановление и обработку данных. Простота проистекает из геометрической регулярности разбиения, а эффективность - за счет хранения только узлов с данными, которые представляют интерес. Основополагающая идея квадродерева - комбинирование одинаковых или сходных элементов данных и кодирование больших однородных совокупностей данных малым количеством битов.

Корневой узел соответствует изображению в целом и имеет четыре дочерних узла, которые ассоциируются с четырьмя квадрантами исходного изображения (обозначаемыми NW - северо-западный, NE - северо-восточный, SW - юго-западный, SE - его-восточный). В свою очередь каждый из дочерних узлов корня дерева также имеет по четыре дочерних узла, ассоциированных с шестнадцать субквадрантами исходного изображения. Дочерние узлы следующего уровня представляют собой шестьдесят четыре квадранта, составляющих исходное изображение и так далее.

Рис. 1: (a) изображение (b) его бинарный образ (c) его квадротомическое разбиение

В сформированном выше описанном способом квадродереве листовым узлам дерева (узлам, соответствующим каждому одиночному пикселу изображения) приписывают цвет связанного с ними пиксела (черный или белый). Если нелистовой узел имеет среди дочерних узлов, узлы как одного так и другого цвета, ему приписывается серый цвет. Если же все дочерние узлы нелистового узла дерева "окрашены" в один и тот же цвет, то такому узлу приписывается этот цвет, а его дочерние узлы исключаются из дерева. Таким образом, в квадродереве могут отсутствовать некоторые ветки, представляющие собой достаточно большие одноцветные области.

Как показано Samet and Tamminen (1985), квадродеревья и их варианты оказываются полезными в различных приложениях таких, как обработка изображений, машинная графика, распознавание образов, роботостроении и картографии.

Рис. 2: Пример квадродерева

 

Построение квадродерева

Рис. 3: (a) первый этап разбиения (b) второй этап разбиния
(c) третий этап разбиения (d) изображение полностью разбито

На каждом этапе построения квадродерева изображение разбивается на четыре квадранта и каждому присваивается одно из следующих значений

• 1) белый --> квадрант полностью белый. Обозначается белым квадратом.
• 2) черный --> квадрант полностью черный. Обозначается черным квадратом.
• 3) серый --> квадрант - смесь черного и белого. Обозначается белым кругом.

На нулевом этапе полному изображению (рисунок 1a) сопоставляется корневой узел дерева (рисунок 4). Далее четырем равновеликим квадрантам первого этапа разбиения (рисунок 3a) ставятся в соответствие дочерние узлы первого уровня. В показанном на рисунках частном случае северо-западный NW -квадрант обозначен белым квадратом, а остальные три - серыми кругами (рисунок 4). На очередно этапе серые квадранты снова подвергаются разбиению (на рисунке 3b для простоты показано лишь разбиение SW -квадранта). Как видно по рисунку 3b SW -квадрант на этом этапе содержит два белых, один черный и один серый подквадранты. Они представлены в дереве на рисунке 4. узлами второго уровня. Единственный серый квадрант снова разбивается. В данном случае это разбиение является последним, т.к. ни один из получившихся в результате подквадрантов не оказался серым (один белый и три черных). Подобным же образом обрабатываются и остальные квадранты изображения всех уровней. Окончательный вид квадродерева показан на рисунке 4.

Рис. 4: Окончательный вид квадродерева

 

Burroughs (1986) и Samet (1990) также упоминают о том, что квадродерево полезно при изменении разрешения объекта. Рассмотрим, например, квародерево на рисунке 4, которое представляет изображение, приведенное на рисунке 1.a. Если мы хотим изменить разрешение этого изображения, нам необходимо просто заменить все серые узлы второго уровня на черные узлы. Результатом будет новое изображение, показанное на рисунке 5.

Рис. 5: Изображение с измененным при помощи квадродерева разрешением

Наконец, еще одним немаловажным достоинством квадродеревьев является также наличие доступных исходных текстов программ и алгоритмов для реализации этой структуры данных (см.исходные тексты).

 

Недостатки квадродерева

Главный недостаток квадродеревьев состоит в том, что почти невозможно сравнить два изображения, которые отличаются, например, лишь поворотом. Это обусловлено тем, что квадродеревья, представляющие такие изображения являются абсолютно различными.

Алгоритмы поворота квадротомированного изображения ограничиваются лишь поворотами на углы, кратные 90 градусам. Повороты на любые другие углы невозможны.

Хотя квадродеревья имеют массу плюсов в ГИС-приложениях, их распространение в других областях сдерживается их недостатками. Большинство проблем связано именно с тем, что при повороте изображения для него приходится заново перестраивать квадродерево. При этом сопоставление квадродеревьев исходного и повернутого изображений становится весьма сложной задачей. Вследствие этого применение квадродеревьев, например, в геометрическом анализе форм и распознавании образов остается достаточно узким.

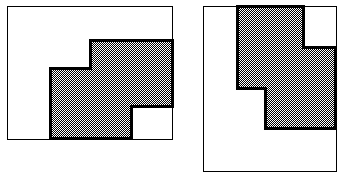
Рис. 6: Исходное и повернутое изображения, различные квадродеревья

 

Что такое ArcView?

ArcView - мощный, легкий в использовании инструмент для обеспечения доступа к географической информации, дает широкие возможности для отображения, изучения, выполнения запросов и анализа пространственных данных. ArcView разработан Институтом Исследований Систем Окружающей Среды (Environmental Systems Research Institute, ESRI), изготовителем ARC/INFO - ведущего программного обеспечения для географических информационных систем (ГИС). Более 25 лет помогает решать разнообразные пространственные задачи. При использовании ArcView не обязательно знать о том, как создаются пространственные данные. ArcView поставляется с уже готовыми к использованию данными. Дополнительные наборы географических данных доступны через ESRI и через различных поставщиков, что позволяет решать любые задачи. И если организация использует данные ARC/INFO, то можно обратиться к этим ресурсам, включая векторные покрытия, библиотеки карт, гриды, изображения и событийные данные.
Работа с пространственными данными
ArcView может быть использована всеми, кому необходима работа с пространственными данными. Главная особенность ArcView - простота загрузки в ArcView табличных данных, типа файлов dBASE и данных с серверов баз, для отображения, запросов, обработки и организации таких данных в удобном для восприятия и анализа виде.
Виды (Views)
Работа в ArcView осуществляется с географическими (распределенными в пространстве) данными на интерактивных картах, называемых Видами. Каждый Вид в ArcView предоставляет уникальную географическую Таблицу содержания, похожую на обычную легенду, облегчающую понимание отображаемых данных, что делает геоинформационную систему довольно простой.
Таблицы (Tables)
Работа с табличными данными в таблицах ArcView организована через элементы управления. Щелкнув по объекту в Виде, выделяются данные в таблице, показывающей нужные атрибуты выбранного объекта. Можно выбрать запись в таблице, и соответствующие объекты выделятся в Виде. Помимо этого, таблицы ArcView обеспечивают полный набор возможностей для получения итоговой статистики, сортировки и запросов.
Диаграммы (Charts)
Диаграммы в ArcView предоставляют средства создания полноценной деловой графики и возможности визуализации данных, полностью интегрированные со средой ArcView. Можно просто щелкнуть по объектам в Виде для добавления их к диаграмме. ArcView позволяет работать одновременно с географическим и табличным представлениями данных, а также с их представлением в виде диаграмм.
Компоновки (Layouts)
Компоновки ArcView позволяют создавать высококачественные, полноцветные карты простым размещением элементов любым из выбранных способов. Компоновки динамичны, потому что имеют связь с представляемыми ими данными. При печати компоновки, любые изменения в картах будут автоматически учтены, и карта будет содержать все внесенные исправления.
Скрипты или тексты программ (Scripts)
Скрипты ArcView являются макрокомандами, написанными на Avenue, языке программирования и среде разработки ArcView. Используя Avenue, можно настроить под свои задачи практически любые элементы управления, начиная от создания новой кнопки, выполняющей скрипт, до создания полного пользовательского приложения, готового для распространения.
Проекты (Projects)
Все компоненты в сеансе работы с ArcView: виды, таблицы, диаграммы, компоновки и скрипты для удобства сохраняются в одном файле, называемом проект. Окно проекта ArcView показывает все компоненты проекта и облегчает управление работой.