ДӘРІС. Термодинамиканың 2-заңы. Энтропия.
Гиббс, Гельмгольц энергиялары. Химиялық тепе-теңдік
Термодинамиканың 2-заңы адамзат тәжірибесінің талдау қорытындысы. Ол заң жылу машинасының пайдалы әсер коэффициентін (ПӘК) зерттеу нәтижесінде ашылды. Жылу машинасы (бу машинасы) жылуды жұмысқа айналдыратын қүрал. Двигатель(қозғағыш) деп циклді түрде жұмыс істейтін және сондықтан бастапқы күйіне периодты түрде қайтып оралатын құралды айтады. Мұндай құралғы қыздырғыштан энергия алып қанша уақыт болса да жұмыс істей алады. Ал қыздырғыш энергияны отынның жануынан алады.
Ыстық денеден салқын денеге жылу көшкенде жұмыс алуға болады, себебі бұл процесс өздігінен жүреді. Бұл кез-келген жылу машинасында іске асатын процесс. Бірақ жылудың бәрі (q1) (жұмысқа айналмайды, оның тек бір бөлігі ғана айналады: А= q1- q2. Қалған бөлігі q2 төменгі температуралы (Т2) денеге көшеді (жылуалғыш немесе суытқыш).Т1 - қыздырғыштың температурасы.
Сөйтіп мұндай машинаның жұмысы тек қана жылу алып және жұмыс атқару емес, сонымен қатар жылудың кейбір мөлшерін q2 төменгі температуралы жылу алғыш денеге беріп отыру болып табылады.
Бұл кезде Т1>Т2 болуы шарт, егер Т1 = T2 болса жылу жұмысқа айналмайды, өйткені; істелінген жұмыстың алған жылуға қатынасы h (ПӘК) – машинаның пайдалы әсер коэффициенті.

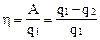 немесе
немесе  (3.1)
(3.1)
Олай болса жылуды толығымен (100%) жұмысқа айналдыру мүмкін емес.
Соның көмегімен термодинамиканың 2-заңының анықтамасын беруге болады: жылу машинасының ең үлкен пайдалы әсер коэффициенті машинаның жұмысына қатысушы заттар мен денелердің түрлеріне немесе табиғатына тәуелді емес, ол тек қана қыздырғыш пен суытқыштың температураларына тәуелді (Карно-Клаузиус теоремасы)
Енді (2.1) – теңдеуді мына түрде жазуға болады: 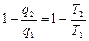 немесе
немесе  немесе
немесе 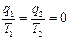 (3.2)
(3.2)
мұндағы  - процестің келтірілген жылуы деп аталады.
- процестің келтірілген жылуы деп аталады.
Термодинамиканың 2-заңының тұжырымдары
«Нәтижесінде жылу толығымен жұмысқа айналатын процесті іске асыру мүмкін емес» (Макс-Планк, Кельвин).
«Идеал жылу машинасының пайдалы әсер коэффициенті қыздырғыш пен суытқыштың температурасымен анықталады» (Сади Карно).
«Барлық әрекеті жылу көзін салқындату арқылы жұмыс өндіруге ғана бейімделген машина жасау мүмкін емес (2-текті мәңгілік двигатель)» (Оствальд). Мысалы: мұхиттардың энергиясының шексіз қорын толық пайдалану мүмкін емес.
Мұхиттардың жылуын пайдалану оның температурасы қоршаған ортадан төмен бола бастаған кезде салқын денеден ыстық денеге жылу берілетін процесс жүргізуге итерер еді, бірақ ол өздігінен жүруі мүмкін емес.
«Температурасы төменірек денеден температурасы жоғарырақ денеге жылу өздігінен берілмейді».
здігінен жүретін процестердің мүмкіншілігі және бағыты. Энтропия
Табиғатта өз еркімен жүретін процестерді өздігінен жүретін немесе табиғи процестер деп атайды.:Жүруі үшін энергия жұмсалуын талап ететін процестерді өздігінен жүрмейтін процестер дейді.
Кез-келген термодинамикалық система үшін оның тұрған жағдайында термодинамикалық процестердің бағытын және өздігінен жүруінің шегін сипаттайтын жалпы критериі болуы қажет. Мысалы, оқшауланған система үшін мұндай критерий ретінде энтропия деп аталатын термодинамикалық функцияны атайды. Басқа жағдайларда тұрған системалар үшін басқа критерий – басқа термодинамикалық параметрлер қолданылады. (Энтропия деген атауды Клаузиус енгізген; грекше ңөзгеріске қабілеттің деген мағына береді). 19-ғасырдың ортасында Клаузиус күй функциясы болатын және өзгерісі q/Т –ға тең термодинамикалық функция – энтропия термодинамиканың 2-заңын бейнелеу үшін өте пайдалы екенін көрсетті.
Энтропия - экстенсивтік термодинамикалық шама, S –таңбасымен белгіленеді және мына қасиеттерімен ерекшеленеді:
Системаның шексіз аз қайтымды өзгерістері үшін  (3.3) және шексіз аз өздігінен жүретін қайтымсыз өзгерістері үшін
(3.3) және шексіз аз өздігінен жүретін қайтымсыз өзгерістері үшін  (3.4)
(3.4)
Энтропия күй функциясы болғандықтан өзгерісі өту жолына тәуелді емес: Система 1-күйден 2-күйге өткенде оның өзгерісі (3.3) – теңдеудің интегралымен бейнеленеді
 (3.5)
(3.5)
Қайтымды процесс үшін (3.5) –ден интеграл алғанда: 
qқайт. – қайтымды процесте сіңірілген жылу.
Термодинамиканың 2-заңының анықтамасы: оқшауланған системаларда оның энтропиясын жоғарылататын процестер ғана өздігінен жүре алады және ондай процестер берілген жағдайларда энтропияның мәні максималдық болатын күйге жеткенше ғана жүре алады ( DS>O).
 ,
, 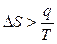 (3.7)
(3.7)
Қайтымды және қайтымсыз процестер үшін теңдеулерді біріктіріп жазсақ:
 ,
,  (3.8)
(3.8)
(3.3) - (3.8) - термодинамиканың 2-заңының математикалық өрнектері.
Оқшауланған системаларда өздігінен жүретін қайтымсыз процестерде dS>0, DS>0.
Энтропия түсінігін шашырап кеткен энергия өлшемі ретінде жиі қолданады, яғни DS мәні үлкен болған сайын пайдалы жұмысқа айналмайтын жылудың көбірек мөлшері кеңістікке тарап кетеді.
Термодинамиканың 1- және 2-заңдарының біріккен теңдеулері
Термодинамиканың 1- заңы Термодинамиканың 2-заңы
dU = dq + dA dq = TdS
қайтымды процесс үшін қайтымсыз процесс үшін кез-келген процесс үшін
dU = TdS + pdV dU< TdS + pdV dU £ TdS + pdV
Бірақ бұдан кері бағытта процесс жүрмейді деген ұғым тумауы керек. Ол тек өздігінен жүрмейді (DS<0), оның жүруі сырттан жұмыс жасалуын талап етеді.
Бөлшектерге (молекулалар, атомдар) әрқашан ретсіз қозғалыс тән болғандықтан, система реттілігі көбірек күйден реттілігі азырақ күйге көшуге тырысады.
Мысал: жылудың ыстық денеден салқын денеге берілісі, газдың араласуы ретсіздігі көбірек күйге көшуіне әкеліп соғады. Ретсіздіктің сан мөлшерін энтропия көосетеді.
3.3 Энтропия және ықтималдық
Термодинамиканың 2-заңы статистикалық заң. Ол уақиғалардың үлкен санын қарастырғанда ғана қолданылады. өздігінен жүретін процестер – бұл біздің айналамызда жүріп жататын ықтималдығы көбірек процестер.
1877 жылы Больцман системаның әр күйіне Термодинамикалық ықтималдық тән деп статистика-лық түсінік енгізді. Термодинамикалық ықтималдық молекулалардың механикалық қозғалыстарының (параметрлерінің таралу тұрғысынан қарағандағы) күйі ретсіз болған сайын артады. Бұл түсінік бойынша энтропияның өсуі системаның өздігінен бір күйден Термодинамикалық ықтималдығы басым екінші күйге өтетінін көрсетеді.
Стаистикалық термодинамикада микроскопиялық параметрлер қолданылады. Системаның макроскопиялық күйі – оның қысымы, температурасы, химиялық құрамы сияқты макроскопиялық параметрлері белгілі болған жағдайда анықталады. Системаның микроскопиялық күйі – оның әрбір бөлшектерінің бір-біріне қатысты сипаттамалары белгілі болған жағдайда анықталады.
Белгілі макроскопиялық күйге микроскопиялық күйлердің өте үлкен саны сәйкес келеді. Бұл микроскопиялық күйлердің саны термодинамикалық ықтималдықты көрсетеді.
Энтропия системаның термодинамикалық ықтималдығының функциясы:
S = klnW (3.9)
Демек, системаның энтропиясы оның күйінің термодинамикалық ықтималдығының логарифміне пропорционал. Мұндағы k – Больцман тұрақтысы.
Бұл маңызды қатынас (3.9) қазіргі статистикалық термодинамиканың негізін қалайды. Термодинамиканың 2-заңын енді былай айтуға болады: Оқшауланған система микроскопиялық күйлерінің саны ең көп болатын ықтималдық күйіне жетуге тырысады.
3.4Термодинамиканың 3-заңы постулат ретінде тұжырымдалады:
Абсолюттік нөл температурада идеал кристалл түріндегі таза заттың энтропиясы нөлге тең.
Бұл 0 К температурада толық реттілік орын алатынын көрсетеді. Белгілі макрокүй тек қана жалғыз микрокүй арқылы іске асады.
W = 1, S = klln1 = 0 (3.10)
(3.10) теңдеу – термодинамиканың 3-заңы
Термодинамиканың 3-заңы барлық таза заттардың абсолюттік энтропиясын кез-келген температурада анықтауға мүмкіндік береді.
Заттардың энтропияларының мәндерін салыстыру үшін оларды стандарттық жағдайда қарайды:
Т = 298К, Р = 101325 Па, ерітінділер үшін концентрациясы немесе активтілігі 1-ге тең.
Осы жағдайда анықталған энтропияны S0298 деп белгілеп стандарттық энтропия деп атайды. өлшем бірлігі –Дж/К моль.






