Наиболее распространенными опенками характеристик положения являются среднее арифметическое выборки (выборочное среднее), выборочная медиана и выборочная мода. В дальнейшем будем, опускать термин «выборочная», имея, однако, в виду, что любая оценка, начисляемая по выборке, является всего лишь приближенным значением соответствующей характеристики генеральной совокупности
Для выборки объема n: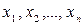 
, среднее арифметическое равно
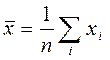
Если выборка представлена в виде статистического ряда, где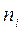 
, есть частота элемента 
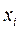, среднее арифметическое вычисляется по формуле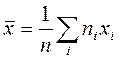 
Модой d называется элемент выборки, имеющий наибольшую частоту.
Пусть 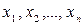вариационный ряд выборки.
Медианой называется число h, которое делит вариационный ряд на две части, содержащие равное число элементов.
Дисперсия определяется по формуле
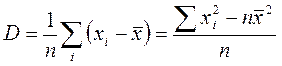
Среднее квадратическое отклонение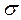 
определяется как арифметический квадратный корень из дисперсии 
.
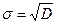В качестве меры относительного разброса данных используют коэффициент вариации
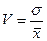или 
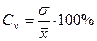
Величину отклонения выборочного показателя (статистики) от его генерального параметра называют статистической ошибкой. Для измерения этой ошибки некоторой статистики квадратичная (стандартная) ошибка статистики (нельзя путать со средним квадратичным отклонением изучаемой случайной переменной). Так, стандартная ошибка среднего арифметического может быть найдена по формуле:
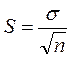
Доверительный интервал
По известным точечным выборочным характеристикам можно построить интервальную оценку или доверительный интервал, в котором с той или иной вероятностью находится генеральный параметр. Вероятности, признанные достаточными для уверенного суждения о генеральных параметрах на основании известных выборочных показателей, называют доверительными. Обычно в медико-биологических исследованиях приемлемым является значение доверительной вероятности Р=0,05 (95%). При этом вероятность выхода истинного значения параметра за пределы этих границ не превышает 1-0,95=0,05 (5%). Величину, дополняющую доверительную вероятность да единицы, обычно обозначают α.
Как известно из центральной предельной теоремы, независимо от распределения исходной совокупности, из которой извлечены выборки, выборочные средние имеют приближенно нормальное распределение. Таким образом, доверительный интервал для выборочного среднего значения находится между границами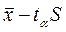 
и 
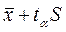, где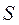 
- стандартная ошибка среднего, 
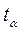- коэффициент Стьюдента, величина, зависящая от объема выборки 
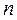(или соответствующего числа степеней свободы 
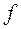) и выбранного уровня доверительной вероятности, определяется по таблицам распределений Стьюдента. Величина коэффициента 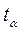, определяется по таблице на уровне α, дополняющем доверительную вероятность до 1,т.е. в случае 95% доверительного интервала на уровне (1 -0,95) = 0,05 с учетом симметрии интервала.
1. Изучалось среднее артериальное давление (мм.рт.ст.) в начальной стадии шока. По случайной выборке объема 50: 112, 110, 107, 103, 108, 109, 111, 110, 103, 103, 109. 102, 113, 106, 105, 108, 104, 99, 112, 112, 103, 101, 98, 100, 97. 98. 100, 98, 107, 108, 99, 98, 92, 98, 110, 106, 105, 102, 100, 101, 100, 95, 100, 105, 100, 102, 102, 99, 97, 100. Найти статистический интервальный ряд распределения и построить гистограмму относительных частот.
2. Изучался рост (см) мужчин возраста 25 лет для сельской местности. По случайной выборке объема 35: 175, 167. 168, 169, 168, 170,174, 173, 177, 172, 174, 167, 173, 172, 171, 171, 170, 167, 174, 177, 171, 172, 173, 169, 171, 173, 173, 168, 173. 172, 166, 164, 168, 172, 174, найти статистический интервальный ряд распределения и построить гистограмму относительных частот.
3. Из продукции, произведенной фармацевтической фабрикой за месяц, случайным образом отобраны 15 коробочек некоторого гомеопатического препарата, количество таблеток в которых оказалось равным соответственно 50,51,48, 52, 50, 49, 50, 47, 50, 51, 49, 50, 52,48,49. Представить эти данные в виде дискретного статистического ряда распределения и построить полигон частот, а также полигон относительных частот.
Литература
Основная литература
1. Адибаев Б.М. Элементы математической статистики и основы теории верятностей. Учебное пособие, Алматы 2004г.
2. Баврин И.И. Краткий курс высшей математики. Учебник для химико-биологических и медицинских специальностей. Москва. 2003г.
3. Павлушков И.В. Основы высшей математики и математической статистики. Учебник для медицинских и фармацевтических вузов. М., 2003г.
4. Е.А.Лукьянова Медицинская статистика. Москва. Издательство Россиского университета дружбы народов.2002г.
5. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. М., «Высшая школа», 2002г.
6. Гмурман В.Е. Теория вероятностей и математическая статистика. М., «Высшая школа, 2001г.
7. Морозов В.Ю. Основы высшей математики и статистики. Москва. Медицина. 2001г.
8. Турецкий В.Я. Математика и информатика. Москва. ИНФРА-М. 2004г.
9. Ремизов А.Н., Максина А.Г. Сборник задач по медицинской и биологической физике. Москва. 2001г.
Дополнительная литература
1. Чистяков В.П. Курс теории вероятностей. М., «Наука», 1982г.
