Оценка значимости (достоверности) результата исследования.
Пусть в результате статистического наблюдения получен ряд из n независимых измерений дискретных случайных величин Х1, Х2, …, Хn (т.е. выборка). Требуется оценить истинное значение а (т.е. для генеральной совокупности, из которой взяты выборки объемом n) измеряемой величины. Это значит:
а) указать такую функцию g (Х1, Х2, …, Хn) от результатов измерений, которая дает достаточно хорошее приближение к значению а. Такая функция называется точечной оценкой или просто оценкой значения а; g (Хi)® a при п ® ¥.
б) указать границы интервала (g -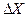 
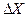, g + ), который с заданной вероятностью Р покрывает истинное значение а. Такая оценка называется доверительной оценкой, вероятность Р – доверительной вероятностью (надежностью, достоверностью), интервал 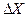(g - , g + 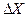) – доверительным интервалом (точностью), а его границы – доверительными границами.
Обычно доверительная вероятность задается в виде одного из трех уровней:
0.95, 0.99 или 0.999.
Если все n измерений величины а произведены с одинаковой точностью (равноточные измерения), то в качестве оценки истинного значения а измеряемой СВ применяют среднее арифметическое значение результатов измерений. Если измерения не являются равноточными, но известны веса измерений, то в качестве оценки истинного значения СВ применяют среднее взвешенное значение.
Таким образом, g (Х1, Х2, …, Хn) = 
.
При бесконечно большом числе измерений истинное значение измеряемой случайной величины равно среднему значению всех случайных величин, т.е.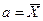 
при 
.
Чем больше величина доверительного интервала ( - 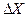, + 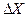), т.е. чем больше задаваемая погрешность результата измерений 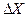, тем с большей надежностью искомая величина а попадет в этот интервал:
.
Естественно, что величина надежности будет зависеть от числа измерений n, а также от величины задаваемой погрешности :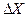
.
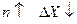Доверительный интервал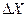 
, который покрывал бы истинное значение а случайной величины Хi с доверительной вероятностью Р, определяется по формуле
.
А для самого истинного значения а случайной величины можно записать выражения
,
или
,
где – среднее значение СВ, s – среднеквадратичное отклонение, n – число измерений СВ, Р – доверительная вероятность, t – коэффициент Стьюдента.
(
) – нижняя граница доверительного интервала, (
) – верхняя граница доверительного интервала.
Коэффициент Стьюдента определяется из таблиц и зависит от доверительной вероятности Р и числа степеней свободы f = n -1. Называется он так в честь ученого, предложившего этот параметр в 1908 г., – английского статистика и химика В.С. Госсета, работавшего в пивоваренной промышленности и публиковавшего свои работы под псевдонимом "Стьюдент" (студент).
Если, например, задана доверительная вероятность 95%, то уровень значимости в этом случае будет равняться 5%. Для этих параметров в таблице приведены для примера значения коэффициентов Стьюдента
| f (или n -1) | ¥ | |||||
| t | 12.71 | 4.3 | 2.57 | 2.23 | 2.09 | 1.96 |
Величину a = 1 – Р, называют уровнем значимости. a – это положительное малое число, которое говорит об ошибке результата исследования.
