ЛЕКЦИЯ № 9
ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ДИСКРЕТНЫХ СИСТЕМ
(продолжение)
План лекции:
севдочастотные характеристики дискретных систем.
2. Методы построения ЧХ дискретных систем.
севдочастотные характеристики дискретных систем.
Из-за своей простоты и удобства использования ЛАФЧХ получили широкое применение при исследовании непрерывных систем. Однако, непосредственное использование ЧХ дискретных систем не может быть выполнено также, как и в случае непрерывных аналогов. Это объясняется тем, что построение дискретных АФЧХ значительно более громоздко, и тем, что эти характеристики не обладают свойством асимптотичности, вследствие чего не могут быть приближенно представлены ломаными линиями. Однако и для дискретных систем оказывается возможным ввести характеристики, которые по методике построения и своим свойствам будут схожи с ЛАФЧХ непрерывных систем. Такие характеристики называются псевдочастотными.
Частотная характеристика дискретной системы полностью определяется значением в диапазоне частот:
; 
.
Чтобы использовать обычную методику построения ЛЧХ вводят так называемую псевдочастоту l и рассматривают псевдочастотные характеристики.
Переход к псевдочастоте делается на основе билинейного преобразования (w-преобразования).
Введем комплексную величину w, связанную с комплексной величиной Z билинейным преобразованием:
; 
(9.1)
Сделав подстановку: 
, получим из предыдущей формулы:
;
; 
;
;
где 
,
представляет собой так называемую относительную псевдочастоту.
При анализе импульсных систем удобно рассматривать абсолютную псевдочастоту:
(9.2)
Тогда: 
и 
.
Чем удобна абсолютная псевдочастота? Она удобна тем, что на малых частотах 
. Поэтому при выполнении условия 
, в расчетах можно заменить псевдочастоту действительной круговой частотой. Это свойство может быть использовано, например, при расчетах реакции импульсной системы на медленно меняющиеся гармонические сигналы на его входе.
Нетрудно видеть из зависимости:
,
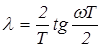что при изменении частоты в пределах: 
, псевдочастота пробегает все значения от -¥ до +¥, а комплексная величина w движется по оси мнимых частот:
, от -j¥ до +j¥.
.
 |
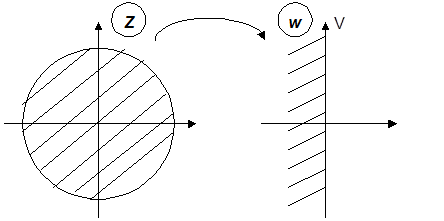Отметим также еще одно замечательное свойство билинейного преобразования.Оно заключается в том, что при таком преобразовании внутренняя часть круга единичного радиуса на плоскости z отображается на левую полуплоскость плоскости w (рис.9.1).
Рис.9.1.
Действительно, пусть w=u+iv, тогда комплексной переменной z определится выражением:
откуда следует, что при
u<0, 
;
u=0, 
;
u>0, 
.
Это свойство оказывается чрезвычайно удобным, так как позволяет использовать традиционные критерии для оценки устойчивости импульсных систем.
Итак, для получения передаточной функции импульсной системы на основе псевдочастоты l, необходимо выполнить подстановку в 
:
,
а затем заменить: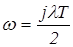 
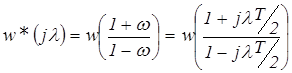
Частотная характеристика W*(jl) в функции псевдочастоты l
называется псевдочастотной характеристикой (ПЧХ).
В w -области передаточная функция дискретной системы есть дробно-рациональная функция jl, причем при изменении w в диапазоне от 
, псевдочастота изменяется в пределах:
.
Таким образом, в области псевдочастот частотные характеристики дискретных систем имеют те же свойства, что и у непрерывных систем. Следовательно, к псевдочастотным характеристикам могут быть применены известные методы синтеза непрерывных систем.
