РАСЧЕТ ЭЛЕКТРОМАГНИТНЫХ
ПЕРЕХОДНЫХ ПРОЦЕССОВ В ЭЛЕКТРИЧЕСКИХ СИСТЕМАХ
Методические указания к выполнению
индивидуальных заданий, курсовых и дипломных проектов.
Архангельск
Рассмотрены и рекомендованы к изданию методической комиссией факультета промышленной энергетики
Архангельского государственного университета
3 марта 2004 г.
Составитель:
В.М. Волков, доц., канд. техн. наук
Рецензент
В.П. Емельянов, доц., канд. техн. наук
УКД 621.3
Волков В.М. Расчет электромагнитных переходных процессов в электрических системах. Методические указания к выполнению индивидуальных заданий, курсовых и дипломных проектов.: Архангельск: Изд-во АГТУ, 2004.-34 с.
Подготовлены кафедрой электроснабжения промышленных предприятий АГТУ.
Предназначены для студентов факультета промышленной энергетики специальности 1004 «Электроснабжение промышленных предприятий» очной и заочной формы обучения.
Ил.I Табл.4. Библиогр.4 назв.
©Архангельский государственный
технический университет, 2004
1. МЕТОДЫ РАСЧЕТА ПЕРЕХОДНЫХ ПРОЦЕССОВ ПРИ
СОХРАНЕНИИ СИММЕТРИИ ТРЕХФАЗНОЙ ЦЕПИ
Общее решение задачи расчета переходных процессов в электрических системах связано с анализом систем нелинейных алгебраических и дифференциальных уравнений высокого порядка. Для решения инженерных задач, такой подход нецелесообразен вследствие большой вычислительной трудоемкости.
Удовлетворительные по точности инженерные решения получают при использовании ряда допущений:
1) сохранении симметрии трехфазной электрической системы;
2) отсутствии насыщения магнитных систем, то есть линейность цепи;
3) пренебрежении токами намагничивания трансформаторов и автотрансформаторов;
4) отсутствии качания синхронных машин;
5) пренебрежении емкостными проводимостями линий электропередач;
6) приближенном учете нагрузок.
Используя данные допущения, расчет переходных процессов при коротких замыканиях целесообразно производить с помощью следующих методов:
налитический метод
Наиболее эффективный подход к анализу токов короткого замыкания - сведение задачи к расчету квазистационарных или стационарных режимов в некоторой расчетной электрической цепи. При этом исследуемый квазистационарный режим соответствует определенному моменту переходного процесса в заданной электрической системе. Для формулирования задачи расчета требуемого момента электромагнитного переходного процесса необходимо представить элементы систем в расчетной электрической цепи параметрами, характеризующими свойства элементов в рассматриваемый момент времени. Расчет следует проводить последовательно в несколько этапов. Особенности каждого расчетного этапа можно рассмотреть при решении задачи.

Рис.1.
Задача 1.
Номинальная мощность станции, питающей потребителей по схеме (рис.1), равна 120 МВ*А. Напряжение генераторов станции 10,5 кВ, их относительная реактивность 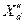 =0,13. Станция работает с номинальной нагрузкой при cosφ=0,8. Присоединенные потребители можно рассматривать как обобщенные промышленные нагрузки, мощности которых составляют Н-1 60 МВ*А, Н-2 40 МВ*А, Н-3 10 МВ*А.
=0,13. Станция работает с номинальной нагрузкой при cosφ=0,8. Присоединенные потребители можно рассматривать как обобщенные промышленные нагрузки, мощности которых составляют Н-1 60 МВ*А, Н-2 40 МВ*А, Н-3 10 МВ*А.
Параметры других элементов схемы:
трансформатор Т-1 60 МВ*А; 115/10,5 кВ;  ;
;
трансформатор Т-2 40 МВ*А; 115/6,5 кВ;  ;
;
трансформатор Т-3 30 МВ*А; 117/35/6,5 кВ;  ;
; 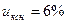 ;
; 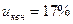 ;
;
линии Л-1 66 км; Л-2 38,5 км; Х=0,4 Ом/км одной цепи.
При трехфазном коротком замыкании в точке К на стороне 35 кВ определить величину начального сверхпереходного тока в месте повреждения. Решение привести в относительных единицах. В исходных данных отсутствуют параметры, характеризующие активное сопротивление элементов, поэтому в расчетах принимаем r=0.
Решение.
Первый этап – составление схем замещения. Основу для получения расчетных цепей (схем замещения) составляет однолинейная схема трехфазной электрической системы. Поскольку трехфазная система принята симметричной, то анализ ее режима достаточно проводить только для одной фазы. Режим расчетной схемы должен моделировать процессы только в одной фазе электрической системы. Структуру расчетной схемы замещения (цепи) определяют из топологии исходной электрической системы. При этом необходимо учитывать равенство напряжений в началах ветвей источников энергии, нагрузок и в местах короткого замыкания. Таким образом, расчетная схема замещения в своей структуре повторяет исходную схему электрической системы и расширяется связями, характеризующими равенство напряжений в началах ветвей генерации, нагрузки и в местах повреждений (рис.2).
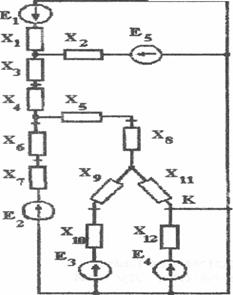 Рис.2.
Рис.2.
Второй этап – вычисление параметров составленной схемы замещения. Параметры расчетных схем определяются характеристиками элементов электрических систем, отвечающих рассматриваемому моменту переходного процесса.
Этот этап наиболее эффективен в случаях расчета начального момента переходного процесса и установившегося режима, которым заканчивается переходный процесс. В начальный момент электромагнитного переходного процесса элементы электрических систем в расчетных схемах представлены следующими моделями:
а) генераторы - активным двухполюсником в виде сверхпереходных (переходных) эдс 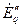 (В) и сопротивления
(В) и сопротивления 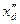 (Ом). Параметры двухполюсника определяют по характеристикам генератора Рн, Uн, cosφн,
(Ом). Параметры двухполюсника определяют по характеристикам генератора Рн, Uн, cosφн,  :
:
 ; (1)
; (1)
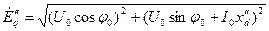 , (2)
, (2)
где индекс "н" определяет номинальные параметры элемента; U0, I0, φ0 -параметры машины в режиме, предшествующем короткому замыканию; причем U0, I0 – фазные параметры режима.
б) двухобмоточные трансформаторы и автотрансформаторы двухполюсником, полное сопротивление которого Z (Ом), его составляющие r и х (Ом) определяют по напряжению uк % и мощности Рк короткого замыкания:

 ; (3)
; (3)
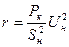 ; (4)
; (4)
 ; (5)
; (5)
При неучете активных сопротивлений
 . (6)
. (6)
в) трехобмоточные трансформаторы и автотрансформаторы - трехлучевой звездой, для которой полные сопротивления лучей ZB, ZC, ZH (Ом) определяются напряжениями короткого замыкания 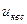 ;
; 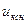 ;
; 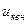 %, а активные сопротивления (Ом) - мощностями короткого замыкания Рквс, Рквн, Рксн;
%, а активные сопротивления (Ом) - мощностями короткого замыкания Рквс, Рквн, Рксн;
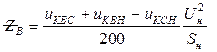 ; (7)
; (7)
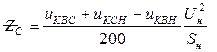 ; (8)
; (8)
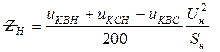 ; (9)
; (9)
 ; (10)
; (10)
 ; (11)
; (11)
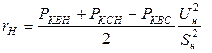 . (12)
. (12)
Значения хВ, хС, хН определяют по формуле (5). Если пренебречь активными сопротивлениями, то хВ, хС, хН можно вычислить по формулам (7), (8), (9);
г) реакторы - двухполюсником, параметры которого х и r (Ом) оценивают характеристикой реактивности хН, потерями на фазу Рк и номинальному току Iн:
 ;
;

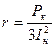 . (13)
. (13)
д) сдвоенные реакторы - трехлучевой звездой, для которой параметры лучей определяются относительной реактивностью х, коэффициентом связи К и отношением х/r:
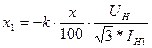 ; (14)
; (14)
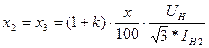 . (15)
. (15)
е) кабельные линии и воздушные линии электропередач протяженностью менее 1000 км - двухполюсником, полное сопротивление Z (Ом) которого определяется удельными
сопротивлениями rуд, худ и длиной линии l по формуле
 (16)
(16)
ж) воздушные линии протяженностью более 1000 км - моделями,
в которых учитывают распределение параметров;
з) асинхронные двигатели - активным двухполюсником в виде сверхпереходных эдс 
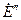 (В) и сопротивлений
(В) и сопротивлений 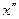 (Ом), определяемых по характеристикам двигателя Р2н, ηн, cosφн, Uн,
(Ом), определяемых по характеристикам двигателя Р2н, ηн, cosφн, Uн, 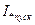 :
:
 ; (17)
; (17)
 . (18)
. (18)
и) синхронные двигатели и компенсаторы - активным двухполюсником в виде сверхпереходных эдс  (В) и сопротивлений
(В) и сопротивлений 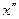 (Ом), определяемых по характеристикам Р2н, ηн, cosφн, Uн,
(Ом), определяемых по характеристикам Р2н, ηн, cosφн, Uн, 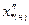 :
:
 ;
;
 ,
,
где знак плюс относится к компенсаторам, знак минус - к двигателям.
При рассмотрении электромагнитных переходных процессов, связанных с включением двигателей, в расчетных схемах эти двигатели представляют только сверхпереходными реактивностями.
к) обобщенная нагрузка - активным двухполюсником, параметры которого 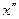 (Ом),
(Ом), 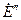 (кВ) определяют по формулам:
(кВ) определяют по формулам:
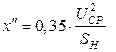 ;
;
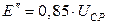 ,
,
где Ucp - среднее значение, кВ, той ступени, на которой включена нагрузка мощностью Sн,MB*A;
л) система бесконечной мощности - активным двухполюсником с параметрами  (В), Zc(Ом):
(В), Zc(Ом):
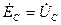 ;
;  ,
,
где  - напряжение системы, поддерживаемое за неизменным сопротивлением Zc.
- напряжение системы, поддерживаемое за неизменным сопротивлением Zc.
Если в состав рассматриваемой электрической схемы входят трансформаторы, то в расчетной схеме все элементы системы представляются моделями, параметры которых должны быть приведены к одному уровню напряжения, выбранному за основной. Приведение параметров моделей осуществляется с помощью следующих соотношений:
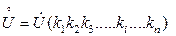 ;
;
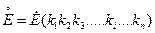 ;
;
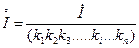 ;
;
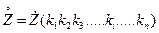 ,
,
где ki - коэффициент трансформации i-го трансформатора, определяемый на холостом ходу отношением линейного напряжения обмотки, обращенной в сторону основной ступени, к линейному напряжению обмотки, обращенной в сторону приводимого элемента;
n - число трансформаторов, включенных между основной ступенью и приводимой.
При выполнении расчетов в системе относительных единиц параметры схем замещения выражают в относительных единицах путем деления именованной величины на базисную. Параметры схемы замещения выражаются в относительных единицах, если определены базисные величины Sб, Uб, Iб, Zб.
Эти величины могут быть выбраны произвольно. Удобнее выбирать только две базисные величины, например Sб и Uб другие параметры вычислять, используя следующие соотношения:
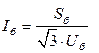 ;
; 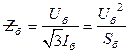 ;
;  ;
; 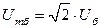 ;
;  .
.
При данном выборе базисных величин все соотношения, справедливые для именованных величин, остаются в силе и для относительных.
При наличии в схемах трансформаторов для решения задач в системе относительных величин следует предварительно привести все именованные величины. На каждом уровне напряжения определяют базисные величины. Если на основном уровне напряжения выбраны SбI и UбI, то на всех других уровнях базисные величины вычисляют по соотношениям:
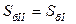 ;
; 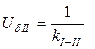 ;
;
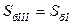 ;
; 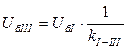 ,
,
где kI-II и kI-III - коэффициенты трансформации трансформаторов, связывающих I и III уровни напряжения соответственно.
Таким образом, выражая параметры элементов в системе относительных единиц, осуществляют и приведение параметров к одному уровню:
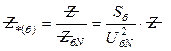 ;
;  ;
;  ;
;  ,
,
где UбN, IбN, ZбN, ImбN, UcpбN - базисные величины того уровня напряжения, на котором находится данный элемент, то есть которому соответствуют величины 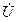 ,
,  ,
,  , Z, r, x,
, Z, r, x, 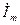 ,
, 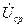 .
.
В соответствии с моделями элементов электрических систем для начального момента Uб1Sб =120 MB*A; Uб1 =10,5 кВ, определим базисные величины на других уровнях:
 кВ;
кВ;
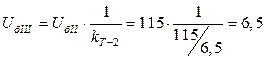 кВ;
кВ;
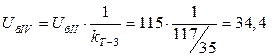 кВ;
кВ;
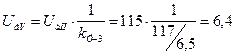 кВ.
кВ.
Выразим параметры схемы замещения в системе относительных единиц, учитывая, что условиями задачи определены только реактивные сопротивления:
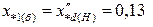 ;
; 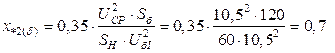 ;
;
 ;
;
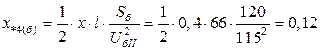 ;
;
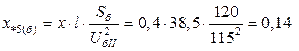 ;
;
 ;
;
 ;
;
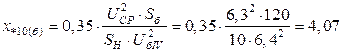 ;
;
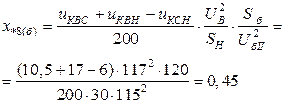 ;
;
 ;
;
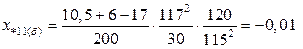 ;
;
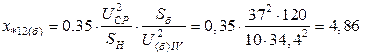 ;
;
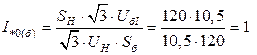 ;
; 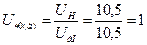 ;
;
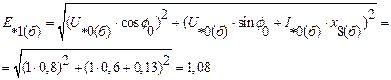 .
.
3. Третий расчетный этап – вычисление токов короткого замыкания на основе полученной схемы замещения.
При полном анализе режима работы расчетной электрической цепи используют следующие методы расчета электрических цепей: методы контурных токов, узловых напряжений и законы Кирхгофа. Если задачи исследования
электромагнитных процессов ограничены расчетом токов короткого замыкания только в одной аварийной ветви или в местах повреждения, то целесообразно использовать метод эквивалентного генератора или методы, основанные на принципе наложения. При рассмотрении коротких замыканий в узлах схемы ток в месте повреждения определяют как сумму токов аварийных ветвей. При использовании метода эквивалентного генератора в качестве выделяемой ветви удобно выбирать не аварийную, а ветвь, связывающую место короткого замыкания с нейтральным узлом схемы. Сопротивление такой ветви равно нулю. Выбор метода при анализе режима работы расчетной схемы связывают с минимумом вычислительных затрат.
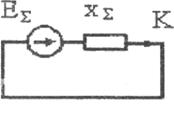 Рис. 3.
Рис. 3.
Для определения тока в месте короткого замыкания используют метод эквивалентного генератора, приводя схему замещения к элементарному виду (рис.3) путем эквивалентных преобразований сопротивлений и эдс последовательно и параллельно включенных ветвей.
Результирующее сопротивление схемы, то есть сопротивление эквивалентного генератора (рис. 2) относительно точки К, определяем из выражения
 ,
,
где знак // определяет сложение параллельно включенных сопротивлений.
(Здесь индексы * и (б) опускаются)
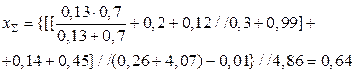 .
.
Результирующая эдс, то есть эдс эквивалентного генератора, вычисляется сложением эдс последовательно и параллельно включенных ветвей:
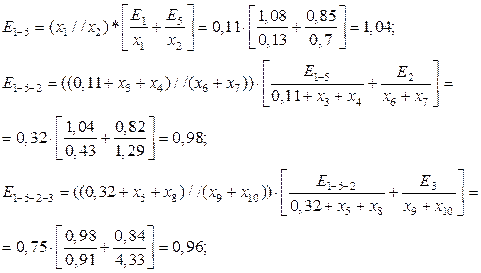
 Относительная величина модуля действующего значения тока короткого замыкания в месте повреждения в соответствии с методом эквивалентного генератора определяется по формуле:
Относительная величина модуля действующего значения тока короткого замыкания в месте повреждения в соответствии с методом эквивалентного генератора определяется по формуле:
 ,
,
где  - сопротивление выделяемой ветви.
- сопротивление выделяемой ветви.
Модуль действующего значения фазного тока короткого замыкания определяют в именованных единицах
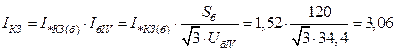 кА.
кА.
Рассмотренный этап используют и для расчета установившихся режимов короткого замыкания. При этом также режим исходной электрической системы моделируется квазистационарным режимом расчетной электрической цепи.

Рис.4
Задача 2.
Определить величину установившегося тока короткого замыкания в точке К электрической системы (рис.4). Параметры элементов электрической системы следующие:
генератор Г - 52 МВ*А; 10,5 кВ; хd = 1,0; АРВ включен, 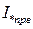 =4;
=4;
система С - источник бесконечной мощности с неизменным напряжением Uc =112 кВ;
трансформатор Т - 60 MB*А, 110/11 кВ, uк = 10,5%;
нагрузка Н - 77 МВ*А;
реактор Р - 10 кВ; 1,0 кА; Х=5%.
Решение.
1. Топология схемы замещения определяется на основе изложенных положений применительно к начальному моменту короткого замыкания.
2. Модели элементов электрической системы в расчетных схемах при установившемся режиме короткого замыкания могут быть следующими:
а) для генератора с АРВ — активный двухполюсник со, следующими параметрами:
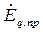 - эдс генератора (В), соответствующая предельному току возбуждения Iпр.в и хd - синхронная реактивность (Ом), если генератор работает в режиме предельного возбуждения, то есть ток в генераторе превосходит критический ток Iкр (А). Если генератор работает в режиме номинального напряжения (ток в генераторе меньше тока критического Iкр), то
- эдс генератора (В), соответствующая предельному току возбуждения Iпр.в и хd - синхронная реактивность (Ом), если генератор работает в режиме предельного возбуждения, то есть ток в генераторе превосходит критический ток Iкр (А). Если генератор работает в режиме номинального напряжения (ток в генераторе меньше тока критического Iкр), то  = UH; Х=0.
= UH; Х=0.
По паспортным данным генератора параметры двухполюсника вычисляют следующим образом:
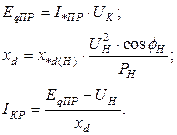
б) Для генератора без АРВ - активный двухполюсник с параметрами

в) Для обобщенной нагрузки, синхронных и асинхронных двигателей - двухполюсник, полное сопротивление которого определяется по формуле
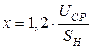 .
.
Модели других элементов электрических систем не отличаются от их моделей для начального момента переходного процесса.
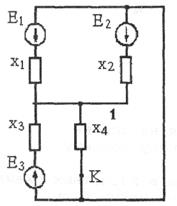 Рис.5.
Рис.5.
При составлении расчетной схемы (рис.5) принимается модель генератора, соответствующая режиму предельного возбуждения, поскольку генератор достаточно близок к месту повреждения.
Принимая в качестве базисных величин
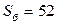 МВА;
МВА;  кВ;
кВ; 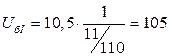 кВ,
кВ,
выразим параметры схемы замещения в системе относительных единиц:
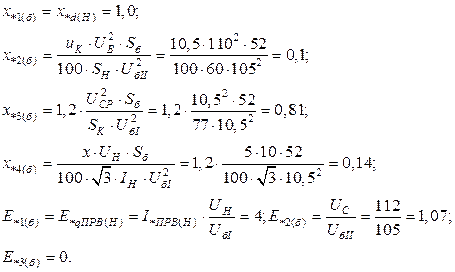
3. Особенность анализа режимов расчетных схем, моделирующих установившиеся режимы короткого замыкания, состоит в решении системы алгебраических уравнений со скачкообразными нелинейностями. Ориентировочно принятый режим работы генераторов с АРВ должен удовлетворять ограничениям по рассчитываемому току в генераторе. Решение таких систем уравнений можно выполнять в следующем порядке.
В зависимости от удаленности генератора от места
повреждения принимается тот или иной режим работы генератора с АРВ, а, следовательно, и соответствующая модель. Вычисляют режим работы расчетной цепи с принятыми моделями генераторов. Если полученные токи в некоторых генераторах с АРВ не удовлетворяют условиям существования выбранных режимов, то для этих генераторов принимают другие режимы и соответствующие модели. Затем рассчитывают схемы с этими моделями. Процесс продолжается до тех пор, пока не установится соответствие между принятыми и рассчитанными режимами для всех генераторов.
Прежде чем определять ток в месте короткого замыкания, оценим правильность выбранного режима работы генератора. Для этого достаточно сравнить критический ток генератора с током, который протекает в генераторе согласно расчетной схеме (см. рис.5).
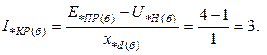
Ток в генераторе наиболее просто определяется из уравнения узловых напряжений, записанного для узла 1:
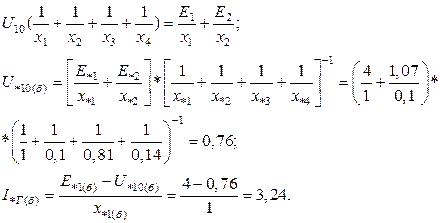
Ток в генераторе ( ) больше тока критического (
) больше тока критического ( ), следовательно, генератор работает в режиме предельного возбуждения. Таким образом, предварительно принятый режим работы генератора соответствует действительности.
), следовательно, генератор работает в режиме предельного возбуждения. Таким образом, предварительно принятый режим работы генератора соответствует действительности.
Определяем ток в месте короткого замыкания

или в именованных единицах модуль действующего значения фазного тока в месте повреждения
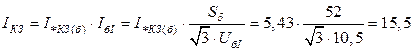 кА
кА
етод спрямленных характеристик
Аналитический подход анализа электромагнитных переходных процессов при использовании метода спрямленных характеристик может быть применен для расчета любого момента переходного процесса. Основу метода спрямленных характеристик составляет возможность характеризовать электрическую машину в любой момент переходного процесса в одномашинной системе некоторыми эдс и реактивностью, не зависящими от параметров внешней цепи. Погрешности таких моделей составляют не более 8%. Однако строго доказать правомерность использования таких моделей для представления переходных процессов не удается. Сравнение с результатами расчетов по более точным методикам показывает, что использование метода спрямленных характеристик позволяет получать удовлетворительные по точности решения и для многомашинных систем.
Рассмотрим особенности расчетных этапов этого метода.
1. Топологию схем замещения определяют на основе положений, изложенных применительно к задачам о начальном моменте переходного процесса. Вследствие невысокой точности результатов, получаемых при использовании метода спрямленных характеристик, в расчетную схему целесообразно вводить эквивалентные укрупненные нагрузки, не выделяя отдельных нагрузочных узлов.
2. Элементы электрических систем в расчетных схемах, согласно методу спрямленных характеристик, можно представить следующими моделями:
а) Генератор, работающий в режиме подъема напряжения, то есть когда ток генератора больше тока критического Iкрt, - активным двухполюсником с параметрами  *, xt* в момент времени t переходного процесса при предшествующем токе возбуждения определяют по кривым (рис.6) для типовых генераторов средней мощности: Et*=f(t); xt* = φ(t).
*, xt* в момент времени t переходного процесса при предшествующем токе возбуждения определяют по кривым (рис.6) для типовых генераторов средней мощности: Et*=f(t); xt* = φ(t).
Если параметры генераторов отличаются от типовых, то эдс и реактивность двухполюсника определяют из соотношении:
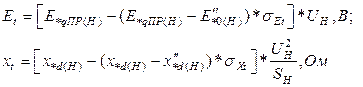
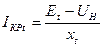 ,А
,А
где  ,
, 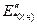 ,
,  ,
,  , Uн, Sн - параметры генератора; σЕt, σxt - коэффициенты, определяемые по кривым (рис.6).
, Uн, Sн - параметры генератора; σЕt, σxt - коэффициенты, определяемые по кривым (рис.6).

Рис. 6.
Если значения постоянных времени для обмотки возбуждения Тв0 генератора существенно отличаются от типовых значений, то величины Et, xt определяют для момента t`: для турбогенераторов 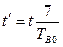 ; для гидрогенераторов
; для гидрогенераторов  .
.
б) Генератор, работающий в режиме номинального напряжения, то есть когда ток в генераторе меньше тока критического Iкрt -активным двухполюсником с параметрами E = UH; x =0.
Модели других элементов системы совпадают с моделями для становившегося режима короткого замыкания.
3. Расчет электромагнитного процесса с использованием метода спрямленных характеристик аналогичен расчету установившегося режима короткого замыкания. В зависимости от удаленности генератора от точки короткого замыкания принимается тот или иной режим работы и соответствующая модель. Рассчитанные токи в генераторах должны удовлетворять принятому режиму. Если соотношения между токами в генераторах и их критическими удовлетворяют выбранным режимам работы генераторов, то расчет закончен. Для тех генераторов, у которых эти соотношения не выполняются, изменяют режим работы и соответственно модели. Затем производится расчет скорректированной схемы и т.д.
етод расчетных кривых
Рассмотренные методы расчета электромагнитных переходных процессов позволяют рассчитывать режим работы всех элементов схемы электрической системы. На практике часто встречается задача анализа переходных процессов только в одной аварийной ветви. Наиболее целесообразен, с точки зрения вычислительных затрат, метод расчетных кривых, позволяющий оценивать ток в месте короткого замыкания в любой момент времени.
Суть метода расчетных кривых состоит в том, что для одиночного генератора, работающего в предшествующем режиме с номинальной нагрузкой, периодическая составляющая тока короткого замыкания однозначно определяется электрической удаленностью генератора от места повреждения. Зависимости периодической составляющей тока генератора от сопротивления Zрасч ветви, за которой рассматривается трехфазное короткое замыкание, представлены в виде расчетных кривых (рис. 7, 8).
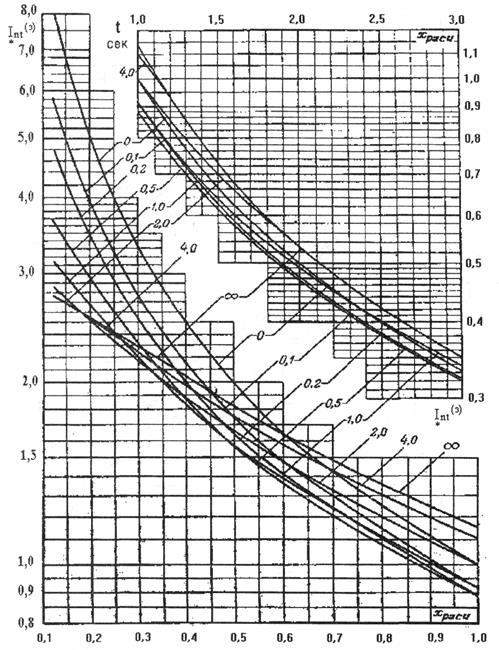 Рис.7.
Рис.7.

Рис. 8.
Эквивалентные преобразования сложных многомашинных систем позволяют получить схему с одним генератором суммарной мощности. Для расчета переходных процессов в таких системах используют зависимость тока генератора от сопротивления. Погрешности расчетов в таких случаях определяются тем, насколько реальные условия для отдельных генераторов отличаются от средних, соответствующих эквивалентному генератору.
Задача 3.
Решить методом расчетных кривых задачу № 1.
При решении необходимо учитывать следующие особенности расчетных этапов:
1. Топологию расчетной схемы определяют в соответствии с положениями, изложенными применительно к задаче о начальном моменте переходного процесса.
2. Для элементов электрических схем при составлении расчетных схем замещения по методу расчетных кривых используют следующие модели:
а) для генераторов - двухполюсник, параметром которого является сверхпереходная реактивность генератора 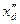 , определяемая по формуле (1);
, определяемая по формуле (1);
б) для обобщенных нагрузок и двигателей, удаленных от места короткого замыкания, - двухполюсник с бесконечно большим сопротивлением. Эти элементы в расчетных схемах отсутствуют;
в) крупные двигатели и компенсаторы, находящиеся вблизи точки короткого замыкания рассматривают как генераторы равновеликой мощности.
Другие элементы электрических схем представляют такими же моделями, как и при расчете начального момента
переходного процесса.
Схема замещения для данной задачи представлена на рис.9.
3. Осуществить эквивалентные преобразования расчетной схемы к схеме пассивного двухполюсника (один конец которого должен совпадать с точкой короткого замыкания), то есть вычислить результирующее сопротивление Z∑ данной схемы относительно точки короткого замыкания.
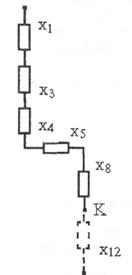
Рис.9.
На основе полученного значения Z∑ вычислить расчетное сопротивление Z*расч, которое определяет периодическую составляющую тока короткого замыкания в месте повреждения по формуле
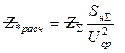 ,
,
где SH∑ - суммарная мощность генераторов схемы, участвующих в питании короткого замыкания;
Ucp - среднее напряжение той ступени, на которой рассматривается точка короткого замыкания.
По соответствующим кривым (см. рис.7), используя интерполирование, для любого момента времени t по значению расчетного сопротивления Zрасч определить относительное значение тока короткого замыкания 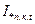 . При Zрасч >3
. При Zрасч >3

Периодическая составляющая тока короткого замыкания в месте повреждения для момента t переходного процесса определяется из выражения
 где
где 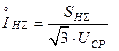
В тех случаях, когда влияния отдельных источников на ток короткого замыкания существенно различны, а также при наличии в схемах источников бесконечной мощности, их необходимо выделять в самостоятельно генерирующие ветви. При этом, если питание места короткого замыкания осуществляется различными источниками через общие ветви, то выделять отдельные генерирующие ветви можно с помощью эквивалентных преобразований звезды в многоугольник. Для каждой выделенной ветви с результирующим сопротивлением Z∑i определяют расчетное сопротивление:
 ,
,
где SH∑i - суммарная мощность генераторов i-ой выделяемой ветви.
По значениям  для всех выделенных ветвей определяют с помощью расчетных кривых относительные значения периодических составляющих токов в отдельных ветвях
для всех выделенных ветвей определяют с помощью расчетных кривых относительные значения периодических составляющих токов в отдельных ветвях 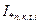 . Тогда величина периодической составляющей тока короткого замыкания в месте повреждения определяется по формуле:
. Тогда величина периодической составляющей тока короткого замыкания в месте повреждения определяется по формуле:
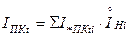 ,
,
где 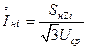 - номинальный ток i-ой генерирующей ветви, а для источников с SH∑ = ∞
- номинальный ток i-ой генерирующей ветви, а для источников с SH∑ = ∞
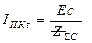 .
.
Выделение генераторов в отдельные ветви основано на допущении независимости протекания процессов в этих ветвях. Такой подход позволяет несколько уточнить расчеты, когда число выделяемых ветвей не превышает двух-трех.
Выразим результирующее сопротивление ветви станции (см.рис.9) относительно точки короткого замыкания:
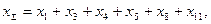
учитывая вычисленные параметры (см. разд. 1.1),
 .
.
Расчетное сопротивление ветви станции:
 .
.
Используя расчетные кривые при 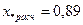 , t =0, находим относительное действующее значение периодической составляющей тока в месте короткого замыкания:
, t =0, находим относительное действующее значение периодической составляющей тока в месте короткого замыкания:
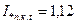 ,
,
в именованных единицах
 кА.
кА.
Полученная величина существенно отличается от решения аналитическим методом. Заниженное значение тока короткого замыкания объясняется, в первую очередь, тем, что не учитывают влияние нагрузки, на выводах которой рассматривается повреждение. Выделяя эту нагрузку в отдельную генерирующую ветвь, можно получить более точное значение.
 .
.
По расчетным кривым (см. рис.7) при 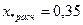 в момент t =0
в момент t =0 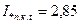 . Определяем ток от нагрузки в месте повреждения:
. Определяем ток от нагрузки в месте повреждения:
 кА
кА
Таким образом, с учетом близости нагрузки к месту короткого замыкания определяем ток в точке К:
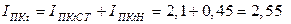 кА.
кА.
2. МЕТОДЫ РАСЧЕТА ПЕРЕХОДНЫХ ПРОЦЕССОВ ПРИ НАРУШЕНИИ СИММЕТРИИ ТРЕХФАЗНОЙ ЦЕПИ
Анализ переходных процессов в несимметричных трехфазных электрических системах основан на использовании метода симметричных составляющих. Решение таких задач сложно, поскольку несимметрия электрических машин приводит к появлению высших гармоник в симметричных составляющих. С целью упрощения расчетов в практике считают, что симметрия нарушена только в одном аварийном элементе системы, и рассматривают переходный процесс,.связанный с появлением этой несимметрии. Такое допущение позволяет сводить расчет переходных процессов к решению систем линейных дифференциальных и алгебраических уравнений. Возникновение несимметричных коротких замыканий и обрыв фаз в электрических системах можно рассматривать как включение в месте в месте повреждения симметричного трехфазного источника эдс, считая при этом, что вся цепь остается симметричной. Таким образом, расчет переходных процессов при нарушении симметрии трехфазной цепи сводится к определению симметричных составляющих в симметричной цепи при включении в исходную схему источников эдс прямой, обратной и нулевой последовательностей.
налитический метод
В инженерной практике задача расчета переходных процессов как при сохранении симметрии трехфазной цепи, так и при нарушении в большинстве случаев ограничена нахождением токов и напряжений только в конкретный момент времени, то есть не требуется получения временных
зависимостей параметров режима, характеризующих весь интервал переходного процесса. Наиболее экономично, с точки зрения вычислительных затрат, свести задачу расчета переходных процессов в исходной системе к анализу квазистационарных режимов расчетной электрической цепи. Для исходной трехфазной электрической системы, обладающей симметрией фаз, использование метода симметричных составляющих формулируется в виде расчетов квазистационарных режимов в трех однофазных цепях. При этом параметры этих (расчетных) цепей должны отражать поведение элементов электрических систем в рассматриваемый момент переходного процесса, связанного с включением источников эдс соответственно прямой, обратной и нулевой последовательностей.
Задача 4.
Определить величину тока в месте повреждения в начальный момент однофазного металлического короткого замыкания в точке К-1 электрической системы (см.рис.1).
Решение.
Первый этап – составление схем замещения для симметричных составляющих токов короткого замыкания.
Топологию расчетных цепей симметричных последовательностей определяют исходной схемой, а также схемами соединения многофазных элементов электрической системы. В топологии расчетных схем необходимо учитывать, что напряжения между нейтральными точками генераторных и нагрузочных ветвей равны нулю. При коротких замыканиях между точкой короткого замыкания и нейтральной точкой в расчетные схемы вводят соответствующие эдс прямой, обратной и нулевой последовательностей.
При обрывах фаз источники эдс симметричных последовательностей вводятся в рассечки соответствующих ветвей расчетных схем.
Режим расчетных схем, сформированных на основе топологии электрической системы и моделей элементов, является неопределенным, поскольку неизвестны величины эдс симметричных последовательностей. Однако задача становится однозначной, если на основе граничных условий для конкретного вида повреждения
устанавливают три соотношения, связывающие между собой режимы работы схем симметричных последовательностей в местах повреждений. Иными словами, определяют зависимости между симметричными составляющими токов и эдс. Основываясь на этих соотношениях, можно исключать неизвестные эдс. Тогда расчет переходного процесса сводится к анализу режима комплексной схемы замещения, включающей в себя схемы прямой, обратной и нулевой последовательностей.
Для рассматриваемой задачи об однофазном коротком замыкании граничные условия данного вида повреждения позволяют установить соотношения между симметричными составляющими тока и напряжения (эдс) в месте короткого замыкания для поврежденной фазы А:
 ;
;
 .
.
Комплексная схема замещения может быть получена соединением схем отдельных последовательностей так, чтобы выполнялись граничные условия. Это достигается, если ветви с неизвестными эдс схем симметричных последовательностей включают последовательно в замкнутый контур.
Второй расчетный этап – определение параметров схем замещения.
Модели элементов электрических систем в расчетных схемах прямой, обратной и нулевой последовательностей должны характеризовать свойства элементов в рассматриваемый момент переходного процесса, связанного с включением в исходную схему источников эдс соответственно прямой, обратной и нулевой последовательностей. Величины эдс источников симметричных последовательностей определяют для каждого вида повреждения на основе граничных условий.
Изложенный этап находит наибольшее применение при расчетах начального момента переходного процесса, когда требуется получить распределение токов во всей схеме. При решении таких задач модели элементов электрических систем в расчетных схемах прямой последовательности ничем не отличаются от моделей, принимаемых при расчете начального момента симметричного переходного процесса.
В расчетных схемах обратной последовательности элементы электрических систем представлены следующей моделью:
Генераторы и синхронные двигатели - двухполюсником с параметром х2:
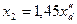 ;
;
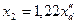 .
.
В упрощенных расчетах принимают  .
.
Индексы 1, 2, 0 определяют параметры, относящиеся к схемам соответственно прямой, обратной и нулевой последовательности.
В расчетных схемах нулевой последовательности элементы электрических систем представляют следующими моделями:
а) Генератор и синхронный двигатель - двухполюсником с параметром х0.
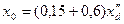 .
.
б) Асинхронный двигатель - двухполюсником с параметром х0, вычисляемым по характеристикам генератора: Р2н, cosφн, ηн, Uн, 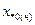 .
.
 .
.
в) Реактор - двухполюсником с параметром Z0, Z0= Z1.
г) Обобщенная нагрузка - двухполюсником с параметром Z0, определяемым сопротивлениями нулевой последовательности компонент нагрузки.
д) Двухобмоточные трансформаторы - двухполюсником с параметром Z0. Для трансформаторов, имеющих со стороны источника эдс нулевой последовательности обмотку, соединенную в треугольник или в звезду без заземленной нейтрали, Z0 = ∞.
При других схемах соединения обмоток Z0 определяется следующим образом:
для схемы Yo/Δ Z0= Z1. Токи нулевой последовательности отсутствуют в цепи за таким трансформатором;
для схемы Yo/Yo Z0= Z1 (если есть заземленная нейтраль в цепи второй обмотки);
для схемы Yo/Y Z0= Zμ0 или Z0 = ∞.
е) Трехобмоточные трансформаторы - трехлучевой звездой. Сопротивления лучей могут иметь конечные значения, если обмотка трансформатора, включенная к
источнику эдс нулевой последовательности, имеет соединение Yo. Для трансформаторов со схемами соединения обмоток Yo/Δ/Yo, Yo/Δ/Δ, Yo/Δ/Y параметры лучей определяют так же, как и для моделей прямой последовательности. При этом следует иметь в виду, что токи нулевой последовательности отсутствуют в цепях обмоток, соединенных треугольником. Поэтому лучи, соответствующие таким обмоткам, должны замыкаться на нейтральную точку схемы. Сопротивление лучей для обмоток, соединенных по схеме Y, принимается равным бесконечности.
ж) Двухобмоточные автотрансформаторы - двухполюсником с параметром Z0. Если обмотки соединены по схеме Yo или Y, то Z0= Z1. В случае соединения обмоток в треугольник Z0 = ∞.
з) Трехобмоточные автотрансформаторы - трехлучевой звездой. Параметры лучей для автотрансформаторов со схемами Yo/Δ/Yo определяются так же, как и у моделей трансформаторов с аналогичными схемами соединения обмоток. У автотрансформаторов со схемами Y/Δ/Y возможна циркуляция токов нулевой последовательности.
и) Воздушные линии электропередач - двухполюсником с параметром Z0:
1) для одноцепной линии без грозозащитных тросов
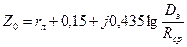 ,
,
где rл - радиус провода фазы;
Dз - глубина возврата тока в земле;
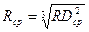 ;
;
R - активное сопротивление провода фазы Ом;
Dср -среднегеометрическое расстояние между проводами фаз.
2) для двухцепных линий без грозозащитных тросов
 ,
,
где DI-II - среднегеометрическое расстояние между фазами линии. l –длина линии. В качестве приближенных оценок сопротивлений нулевой последовательности можно использовать следующие:
для одноцепной линии с грозозащитными тросами х0 =3 х1;
без тросов х0 =3,5 х1;
для двухцепной линии с грозозащитными тросами X0 =4 х1;
без тросов X0 =5,5 х1.
к) Кабельные линии - двухполюсником, параметры которого выражены следующим образом:
r0 = 10 r1; х0 =(3,5…4,6) х1.
С учетом моделей элементов для рассматриваемой задачи приведена комплексная схема замещения (рис.10). Параметры схемы замещения прямой последовательности определены в разд.1.1.

Рис.10. 41
Принимаем, что для всех элементов схемы х2 = х1
Определяем параметры схемы замещения нулевой последовательности:
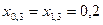 ;
; 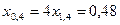 ;
; 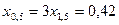 ;
;
 ;
; 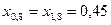 ;
; 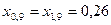 ;
;  .
.
Третий этап – вычисление токов короткого замыкания на основе полученных схем замещения. Расчет комплексной схемы можно проводить при использовании любых методов анализа электрических цепей. Без применения ЭВМ решение задачи удобнее выполнять, используя метод эквивалентного генератора. В этом случае токи и напряжения симметричных последовательностей в местах повреждения выражают через результирующие эдс (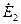 ) и сопротивления Z1∑, Z2∑, Z3∑ схем симметричных последовательностей. Выражения для симметричных составляющих токов и напряжений в месте повреждения приведены в табл.1. Результаты относятся к особой фазе А, отличающейся по условиям повреждения от других фаз, в случае, когда короткое замыкание происходит через дугу. Параметры режима работы фаз через симметричные составляющие определяем с помощью известных соотношений:
) и сопротивления Z1∑, Z2∑, Z3∑ схем симметричных последовательностей. Выражения для симметричных составляющих токов и напряжений в месте повреждения приведены в табл.1. Результаты относятся к особой фазе А, отличающейся по условиям повреждения от других фаз, в случае, когда короткое замыкание происходит через дугу. Параметры режима работы фаз через симметричные составляющие определяем с помощью известных соотношений:

где a = ej120.
Для расчета тока в месте короткого замыкания (задача N4) воспользуемся решениями по методу эквивалентного генератора:
 .
.
Определяем результирующее сопротивление схемы замещения прямой последовательности относительно места повреждения: 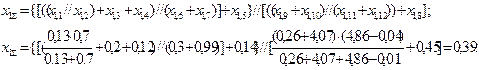
Используя промежуточные результаты (задача N1), вычисляем результирующую эдс: 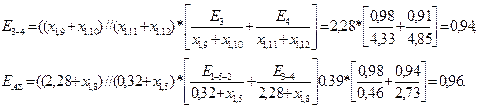
Учитывая, что для всех элементов схемы x2 = x1, получаем результирующее сопротивление схемы замещения обратной последовательности относительно точки короткого замыкания
x2∑= x2∑=0,39.
Результирующее сопротивление схемы замещения нулевой последовательности относительно точки короткого замыкания.

С учетом граничных условий для данного вида повреждения определяем ток аварийной фазы А:
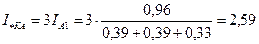 ;
;
в именованных единицах
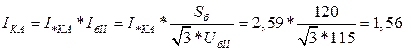 кА.
кА.






