бщие сведения
Математическая формулировка задачи нелинейного программирования может быть представлена как задача отыскания наибольшего или наименьшего значения функции многих переменных:
 (1)
(1)
где функция  является количественной оценкой представляющего интерес качества объекта оптимизации.
является количественной оценкой представляющего интерес качества объекта оптимизации.
На независимые переменные  в общем случае можно наложить различные ограничения в виде равенств:
в общем случае можно наложить различные ограничения в виде равенств:
 (2)
(2)
или неравенств:
 (3)
(3)
или же тех и других одновременно.
Для случая, когда аналитический вид соотношений (1), (2) и (3) известен и не слишком сложен и если, в особенности, число независимых переменных  невелико, всегда можно с большим или меньшим успехом использовать для решения оптимальной задачи аналитические методы. Особые трудности возникают тогда, когда соотношение (1), определяющее значение критерия оптимальности для заданной совокупности значений независимых переменных
невелико, всегда можно с большим или меньшим успехом использовать для решения оптимальной задачи аналитические методы. Особые трудности возникают тогда, когда соотношение (1), определяющее значение критерия оптимальности для заданной совокупности значений независимых переменных  , не может быть записано в явном виде. Задачи такого типа, т.е. с нелинейными и трудновычислимыми соотношениями могут быть решены только численными методами с применением средств вычислительной техники.
, не может быть записано в явном виде. Задачи такого типа, т.е. с нелинейными и трудновычислимыми соотношениями могут быть решены только численными методами с применением средств вычислительной техники.
К одному из эффективных методов нелинейного программирования можно отнести численный метод сканирования.
Метод сканирования заключается в последовательном просмотре значений критерия оптимальности в ряде точек, принадлежащих области изменения независимых переменных, и нахождении среди этих точек такой, в которой критерий оптимальности имеет минимальное (максимальное) значение..
Основным достоинством метода сканирования является то, что при его использовании с достаточно «густым» расположением исследуемых точек всегда гарантируется отыскание глобального оптимума. Другое существенное достоинство – независимость поиска от вида оптимизируемой функции.
Программа численного метода сканирования для решения задачи нелинейного программирования вида:
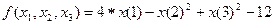 (8)
(8)
при ограничениях:
 (9)
(9)
представлена на рисунке 1.

Рисунок 1.
В программе,рисунок 1, введены следующие обозначения:
 длина шага по каждой переменной
длина шага по каждой переменной  ;
;
 точность решения;
точность решения;
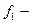 начальное приближение функции многих переменных.
начальное приближение функции многих переменных.
При запуске программы на счет по команде  результат счета получается в окне команд системы MATLAB (рисунок 2):
результат счета получается в окне команд системы MATLAB (рисунок 2):
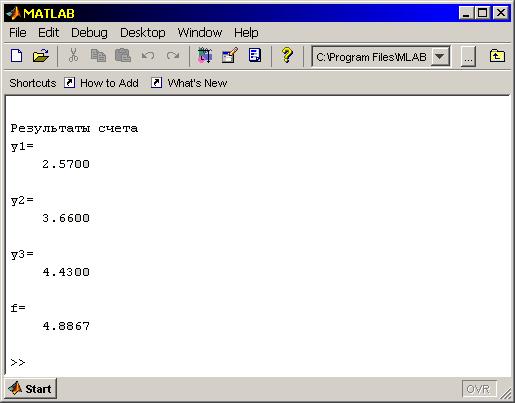
Рисунок 2.
Из рисунка 2 видно, что численное значение первой переменной функции равно 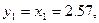
численное значение второй переменной
 .
.
а численное значение третьей переменной

Однако в системе MATLAB данная задача нелинейного программирования, показанная на рисунке 1, может быть решена с помощью функции fmincon.
Программа с использованием функции fmincon дается на рисунке 3, результаты счета показаны на рисунке 4.

Рисунок 3.

Рисунок 4.
Варианты задания
Таблица № 1
| № вари анта | Экстре- мум | Функция

| Ограничения | Начальное приближение |
| min | 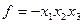
| 
| 
| |
| min | 
| 
| 
| |
| min | 
| 
| 
| |
| min | 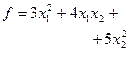
| 
| 
| |
| min | 
| 
| 
| |
| min |  
| 
| 
| |
| min | 
| 
| 
| |
| min |  
| 
| 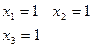
| |
| min | 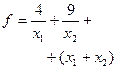
|

|

| |
| min | 
| 
|

|
В программе (рисунок 3) имеются две файл – функции. Одна файл – функция содержит минимизируемую функцию (8), другая с заданными ограничениями (9). Для ограничений  должно выполняться условия
должно выполняться условия  , для ограничений
, для ограничений  необходимо выполнение условий
необходимо выполнение условий  Запуск программы на счет осуществляется по команде
Запуск программы на счет осуществляется по команде  .
.
Результаты счета представленные на рисунке 2 и рисунке 4 имеют незначительную разницу. Значение  (рисунок 4) больше нуля свидетельствует о том, что решение успешно найдено.
(рисунок 4) больше нуля свидетельствует о том, что решение успешно найдено.
рограмма работы
4.2.1 Набрать программу решения задачи нелинейного программирования (функция и ограничения задаются преподавателем из таблицы №1) в M-File системы Matlab (рисунок 1) и получить результат счета.
4.2.2 Набрать программу задачи нелинейного программирования, полученной по заданию преподавателя, в M-File с использованием функции fmincon (рисунок 3) и получить результат счета.
орядок и методика выполнения работы
6.3.1 При запуске программы (рисунок 1) на счет необходимо выполнить команду Debug – Save – Run.
6.3.2 При запуске программы (рисунок 3) на счет необходимо выполнить команду Debug – Save – Run.
одержание отчета
4.4.1 Краткое описание метода сканирования;
4.4.2 Программа метода сканирования и программы с использованием функции fmincon;
4.4.3 Графическое изображение окон Command Window с результатами счета.
4.5 Контрольные вопросы
4. 5.1 В чем заключается сущность метода сканирования?
4.5.2 Достоинства метода сканирования?
4.5.3 В чем заключается разница программы метода сканирования и программы задачи нелинейного программирования с использованием функции fmincon.
4.5.4 Какой командой осуществляется счет по программе задачи нелинейного программирования.
4.5.5 Какие ограничения используются в задачах нелинейного программирования.






