лементы линейной алгебры и аналитической геометрии
11-20. В пирамиде SABC: треугольник АВС – основание пирамиды, точка S – ее вершина. Даны координаты точек A, B, C, S. Сделать чертеж. Найти:
1) длину ребра АВ;
2) угол между ребрами АВ и AS;
3) угол наклона ребра AS к основанию пирамиды;
4) площадь основания пирамиды;
5) объем пирамиды;
6) уравнение прямой АВ;
7) уравнение плоскости АВС;
8) проекцию вершины S на плоскость АВС;
9) длину высоты пирамиды.
11. А(-2;0;0); В(0;3;0); C(0;0;1); S(0;2;3).
12. А(4;0;0); В(0;-8;0); C(0;0;2); S(4;6;3).
13. А(-2;0;0); В(0;6;0); C(0;0;2); S(-1;6;4).
14. А(1;0;0); В(0;2;0); C(0;0;2); S(1;1;4).
15. А(-3;0;0); В(0;-2;0); C(0;0;1); S(-2;-1;3).
16. А(6;0;0); В(0;-3;0); C(0;0;2); S(4;-3;4).
17. А(3;0;0); В(0;-6;0); C(0;0;1); S(1;-3;3).
18. А(-4;0;0); В(0;4;0); C(0;0;2); S(-2;4;3).
19. А(-6;0;0); В(0;2;0); C(0;0;3); S(-3;2;5).
20. А(-1;0;0); В(0;5;0); C(0;0;2); S(-1;3;4).
41-50. На плоскости дана линия своим уравнением в полярной системе координат r=r(φ). Требуется: 1) построить линию по точкам, давая φ допустимые значения через промежуток  , начиная от φ =0 до φ =2 π; 2) найти уравнение данной линии в прямоугольной системе координат, у которой начало совпадает с полюсом, а положительная полуось абсцисс – с полярной осью; 3) по полученному уравнению определить какая это линия.
, начиная от φ =0 до φ =2 π; 2) найти уравнение данной линии в прямоугольной системе координат, у которой начало совпадает с полюсом, а положительная полуось абсцисс – с полярной осью; 3) по полученному уравнению определить какая это линия.
41.  . 42.
. 42.  .
.
43. 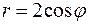 . 44.
. 44.  .
.
45. 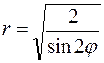 . 46.
. 46.  .
.
47.  . 48.
. 48.  .
.
49. 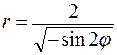 . 50.
. 50.  .
.
51-60. Дана система линейных уравнений: 
Доказать ее совместность и решить тремя способами: 1) методом Гаусса; 2) средствами матричного исчисления; 3) по правилу Крамера.
51. 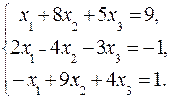 52.
52. 
53. 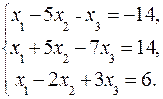 54.
54. 
55.  56.
56. 
57.  58.
58. 
59.  60.
60. 
71-80. Найти собственные значения и собственные векторы линейного преобразования, заданного в некотором базисе матрицей А.
71.  72.
72. 
73.  74.
74. 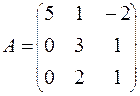
75.  76.
76. 
77. 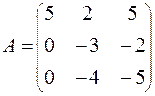 78.
78. 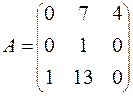
79.  80.
80. 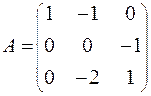
91-100. Дано комплексное число a. Требуется: 1) записать число a в  алгебраической и тригонометрической формах; 2) найти все корни уравнения z3+a=0.
алгебраической и тригонометрической формах; 2) найти все корни уравнения z3+a=0.
91.  . 92.
. 92.  .
.
93.  . 94.
. 94.  .
.
95.  . 96.
. 96.  .
.
97.  . 98.
. 98.  .
.
99.  . 100.
. 100.  .
.
101-105. Построить график функции 
 преобразованием графика функции
преобразованием графика функции 
101. 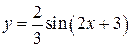 ; 102.
; 102.  ;
;
103.  ; 104.
; 104. 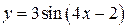 ;
;
105.  .
.
106-110. Построить график функции 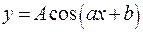 преобразованием графика функции
преобразованием графика функции  .
.
106.  107.
107.  ;
;
108.  109.
109.  ;
;
110.  .
.
111-120. Найти пределы функций, не пользуясь правилом Лопиталя.
111. а)  ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
112. а)  ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
113. а)  ; б)
; б) 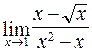 ;
;
в) 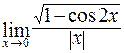 ; г)
; г)  .
.
114. а)  ; б)
; б)  ;
;
в) 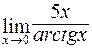 ; г)
; г) 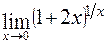 .
.
115. а)  ; б)
; б) 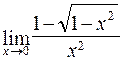 ;
;
в)  ; г)
; г)  .
.
116. а)  ; б)
; б)  ;
;
в)  ; г)
; г) 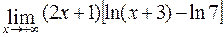 .
.
117. а)  ; б)
; б)  ;
;
в)  ; г)
; г) 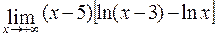 .
.
118. а)  ; б)
; б) 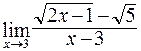 ;
;
в) 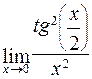 ; г)
; г)  .
.
119. а) 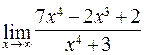 ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
120. а)  ; б)
; б)  ;
;
в)  ; г)
; г) 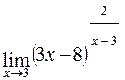 .
.
131 – 140. Задана функция y=f(x). Найти точки разрыва функции, если они существуют. Сделать чертеж.
131. 
132. 
133. 
134. 
135. 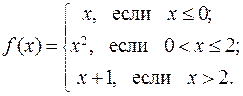
136. 
137. 
138. 
139. 
140. 
2. Производная и её приложение
141-150. Найти производные  данных функций.
данных функций.
141. а)  ; б)
; б)  ;
;
в)  ; г)
; г)  ; д)
; д)  .
.
142. а)  ; б)
; б)  ; в)
; в)  ;
;
г)  ; д)
; д) 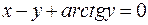 .
.
143. а)  ; б)
; б) 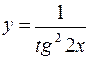 ; в)
; в)  ;
;
г)  ; д)
; д)  .
.
144. а) 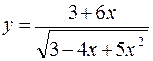 ; б)
; б)  ;
;
в) 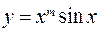 ; г)
; г)  ; д)
; д)  .
.
145. а)  ; б)
; б)  ; в)
; в)  ;
;
г)  ; д)
; д)  .
.
146. а)  ; б)
; б)  ;
;
в)  ; г)
; г)  ; д)
; д)  .
.
147. а)  ; б)
; б)  ;
;
в)  ; г)
; г) 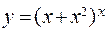 ;
;
д)  .
.
148. а)  ; б)
; б)  ;
;
в)  ; г)
; г) 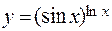 ; д)
; д) 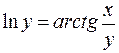 .
.
149. а) 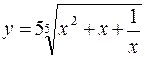 ; б)
; б)  ; в)
; в)  ;
;
г)  ; д)
; д)  .
.
150. а)  ; б)
; б) 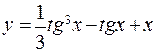 ;
;
в)  ; г)
; г)  ;
;
д)  .
.
151-160. Найти  и
и 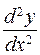 .
.
151. а)  ; б)
; б)  .
.
152. а) 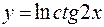 ; б)
; б) 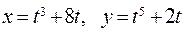 .
.
153. а)  ; б)
; б)  .
.
154. а)  ; б)
; б)  .
.
155. а)  ; б)
; б)  .
.
156. а)  ; б)
; б)  .
.
157. а) 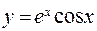 ; б)
; б)  .
.
158. а)  ; б)
; б)  .
.
159. а)  ; б)
; б) 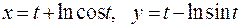 .
.
160. а)  ; б)
; б)  .
.
риложения дифференциального исчисления
101-110. Исследовать методами дифференциального исчисления функцию и, используя результаты исследования, построить ее график.
191.  . 192.
. 192.  .
.
193.  . 194.
. 194.  .
.
195. 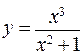 . 196.
. 196.  .
.
197.  . 198.
. 198.  .
.
199.  . 200.
. 200.  .
.
ифференциальное исчисление функций нескольких переменных
231. Дана функция  .
.
Показать, что  .
.
232. Дана функция  .
.
Показать, что  .
.
233. Дана функция  .
.
Показать, что  .
.
234. Дана функция  .
.
Показать, что  .
.
235. Дана функция  .
.
Показать, что 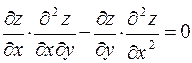 .
.
236. Дана функция  . Показать, что
. Показать, что  .
.
.
237. Дана функция  .
.
Показать, что  .
.
238. Дана функция  .
.
Показать, что  .
.
239. Дана функция  .
.
Показать, что  .
.
240. Дана функция  .
.
Показать, что 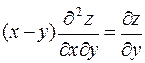 .
.
251-260. Найти наименьшее и наибольшее значения функции z=f(x, y) в замкнутой области D, заданной системой неравенств. Сделать чертеж.
251. z=x 2 +y 2 - 9 xy+ 27; 0≤ x ≤3, 0≤ y ≤3.
252. z=x 2 + 2 y 2 + 1; x ≥0, y ≥0, x + y ≤3.
253. z= 3-2 x 2 -xy - y 2; x ≤1, у ≤ х, у ≥0.
254. z=x 2 + 3 y 2+x-y; x ≥1, y ≥-1, х+y ≤1.
255. z=x 2 + 2 xy +2 y 2; -1≤ x ≤1, 0≤ y ≤2.
256. z= 5 x 2 - 3 xy + y 2 + 4; x ≥-1, y ≥-1, х+y ≤1.
257. z= 10+2 xy - x 2; 0≤ y ≤4- x 2.
258. z=x 2+2 xy -y 2 + 4 x; x ≤0, y ≤0, х+y +2≥0.
259. z=x 2 + xy -2; 4 x 2-4≤ y ≤0.
260. z=x 2+ xy; -1≤ x ≤1, 0≤ y ≤3.
261-270. Дана функция z=z(x, y), точка А(х0, у0) и вектор  . Найти: 1)
. Найти: 1)  в точке A; 2) производную в точке A по направлению вектора
в точке A; 2) производную в точке A по направлению вектора  .
.
261. 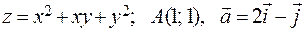 .
.
262.  .
.
263. 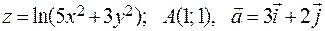 .
.
264. 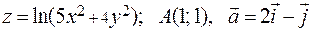 .
.
265.  .
.
266.  .
.
267.  .
.
268. 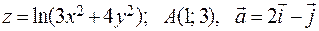 .
.
269.  .
.
270.  .
.
5. Неопределённый и определённыё интегралы
281-290. Найти неопределенные интегралы. В двух примерах (пункты а и б) проверить результаты дифференцированием.
281. а)  ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
282. а)  ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
283. а)  ; б)
; б)  ;
;
в)  ; г)
; г) 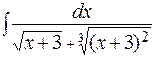 .
.
284. а)  ; б)
; б)  ;
;
в) 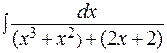 ; г)
; г)  .
.
285. а)  ; б)
; б) 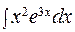 ;
;
в)  ; г)
; г) 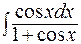 .
.
286. а)  ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
287. а)  ; б)
; б) 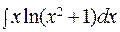 ;
;
в)  ; г)
; г)  .
.
288. а)  ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
289. а)  ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
290. а)  ; б)
; б) 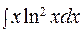 ;
;
в)  ; г)
; г)  .
.
301-310. Вычислить несобственный интеграл или доказать его расходимость.
30 1.  . 30 2.
. 30 2.  .
.
30 3.  . 30 4.
. 30 4.  .
.
30 5.  . 306.
. 306.  .
.
30 7. 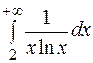 .
.  30 8.
30 8.  .
.
30 9.  . 310.
. 310.  .
.
ифференциальные уравнения
321-330. Найти общее решение дифференциального уравнения.
321.  . 322.
. 322.  .
.
323.  . 324.
. 324.  .
.
325. 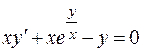 . 326.
. 326. 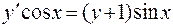 .
.
327.  . 328.
. 328.  .
.
329. 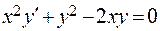 . 330.
. 330.  .
.
341-350. Найти частное решение дифференциального уравнения  , удовлетворяющее начальным условиям
, удовлетворяющее начальным условиям  ,
, 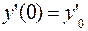 .
.
341.  ;
; 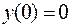 ,
, 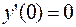 .
.
342.  ;
;  ,
,  .
.
343.  ;
; 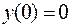 ,
, 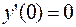 .
.
344.  ;
; 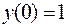 ,
, 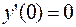 .
.
345.  ;
; 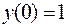 ,
,  .
.
346.  ;
; 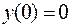 ,
, 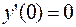 .
.
347.  ;
; 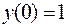 ,
, 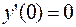 .
.
348.  ;
;  ,
,  .
.
349.  ;
; 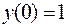 ,
,  .
.
350.  ;
;  ,
,  .
.






