Наибольшему тепловому воздействию струй двигательной установки подвергаются газоотражатели и газоотводные устройства, воспринимающие на себя силовое и тепловое воздействие отводимой от ракеты газовой струи.
Тепловое воздействие на газоотражатели характеризуется следующими данными:
· плотность теплового потока составляет, в среднем,  ;
;
· суммарное тепловое воздействие 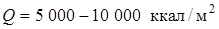 ;
;
· время теплового воздействия составляет от  до
до 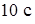 .
.
Плотность теплового потока на отражателях распределяется аналогично давлению на поверхности. Это может быть проиллюстрировано приближенной эмпирической формулой (Я.И. Колтунов)
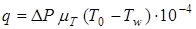 ,
,
где 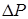 – давление на отражателе
– давление на отражателе 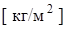 ;
; 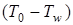 – разность температур газа и стенки;
– разность температур газа и стенки; 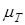 – характеристика топлива, зависящая от его теплотворной способности
– характеристика топлива, зависящая от его теплотворной способности 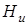 .
.
При 
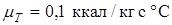
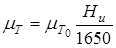 ;
;
Для определения суммарного теплового воздействия необходимо интегрирование произведения переменных величин по времени действия сверхзвукового участка струи (до окончания теплового воздействия при 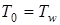 ):
):
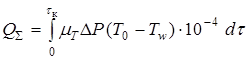 ;
;
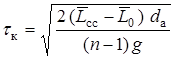 ,
,
где  – длина сверхзвукового участка струи;
– длина сверхзвукового участка струи;  – начальное расстояние сопла от преграды;
– начальное расстояние сопла от преграды;  – перегрузка ракеты при старте.
– перегрузка ракеты при старте.
Тепловое воздействие на газоотводные трубы характеризуется:
· плотностью теплового потока  ;
;
· суммарными тепловыми нагрузками 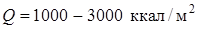 за время действия от
за время действия от 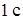 до
до  .
.
Параметры теплового воздействия на поверхности газоотводных труб и газоходов были получены в ходе отработки экспериментальных шахтных пусковых установок. При натурных измерениях определялся весь комплекс параметров, возникающих при взаимодействии струй двигательной установки с элементами пускового устройства (газодинамических, тепловых, акустических, вибрационных). Это позволило выявить специфику тепловых процессов при старте и связать зависимости, полученные при старте, с ранее установленными для изученных течений.
Одной из особенностей в условиях теплообмена является запыленность потока частицами бетона, наличие больших объемов газа с температурой, близкой к температуре торможения, то есть то, что делает заметным вклад в суммарный тепловой поток лучистой составляющей (до 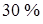 ). Однако тепловое воздействие определяет, в основном, конвективный теплообмен, который при условиях старта имеет свою специфику и некоторые новые свойства. Эти свойства, в первую очередь, появляются в силу действия такого фактора, как акустическая энергия газовой струи, а также больших градиентов давления на поверхности действия газовых струй и пульсаций давления, вызываемых этим действием.
). Однако тепловое воздействие определяет, в основном, конвективный теплообмен, который при условиях старта имеет свою специфику и некоторые новые свойства. Эти свойства, в первую очередь, появляются в силу действия такого фактора, как акустическая энергия газовой струи, а также больших градиентов давления на поверхности действия газовых струй и пульсаций давления, вызываемых этим действием.
3.3.1. Схема процесса теплопередачи от газового потока к конструкциям
Приведенная выше формула для оценки теплового потока далеко не отражает существа процесса теплоотдачи от газа к стенке, а также влияния на него параметров газа и масштабного фактора. Поэтому рассмотрим " классическую " схему механизма теплопередачи от газа к стенке. На рис.3.27 представлена схема течения струи у стенки и распределение параметров в пограничном слое.
Теплопередача происходит в пограничном слое  и ее интенсивность зависит как от уровня параметров потока, так и от градиента изменения параметров в пограничном слое на толщине
и ее интенсивность зависит как от уровня параметров потока, так и от градиента изменения параметров в пограничном слое на толщине  .
.
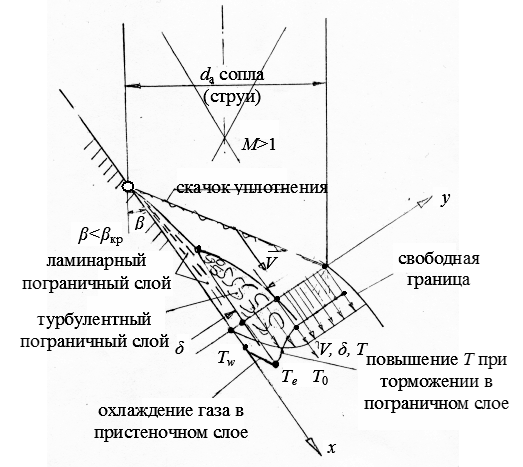
Рис.3.27. Схема течения струи у стенки и распределение параметров
в пограничном слое
Частицы газа тормозятся на стенке ( ). По толщине пограничного слоя режим течения определяется числом Рейнольдса
). По толщине пограничного слоя режим течения определяется числом Рейнольдса  , то есть отношением сил инерции к силам вязкости. Если
, то есть отношением сил инерции к силам вязкости. Если 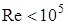 , то течение в пограничном слое слоистое, с устойчивыми траекториями частиц – ламинарное. При числах Рейнольдса
, то течение в пограничном слое слоистое, с устойчивыми траекториями частиц – ламинарное. При числах Рейнольдса 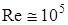 течение неустойчивое (переходный режим); при
течение неустойчивое (переходный режим); при 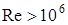 – течение в пограничном слое турбулентное.
– течение в пограничном слое турбулентное.
Температура газа в пограничном слое из-за торможения возрастает от термодинамической 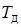 до температуры восстановления
до температуры восстановления 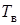 , близкой к температуре торможения
, близкой к температуре торможения  . Однако для теплопроводной стенки в ее непосредственной близости в ламинарном подслое температура газа падает, вследствие теплопередачи в стенку, от значения
. Однако для теплопроводной стенки в ее непосредственной близости в ламинарном подслое температура газа падает, вследствие теплопередачи в стенку, от значения 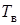 до значения
до значения 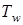 непосредственно на стенке (см. эпюру на рис.3.27).
непосредственно на стенке (см. эпюру на рис.3.27).
Плотность теплового потока определяется формулой
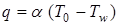 .
.
При всей простоте формулы, определяющей теплоотдачу от газа к стенке при температурном перепаде 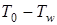 , следует, однако, обратить внимание на то, что вся сложность механизма теплопередачи состоит в сложности определения коэффициента
, следует, однако, обратить внимание на то, что вся сложность механизма теплопередачи состоит в сложности определения коэффициента 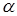 . Этим коэффициентом должно определяться влияние на теплообмен газодинамических параметров обтекания, теплофизических свойств газа переменных по толщине погранслоя и др. Поэтому определение значения
. Этим коэффициентом должно определяться влияние на теплообмен газодинамических параметров обтекания, теплофизических свойств газа переменных по толщине погранслоя и др. Поэтому определение значения 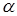 является сложной экспериментальной задачей с воспроизведением критериев моделирования.
является сложной экспериментальной задачей с воспроизведением критериев моделирования.
Коэффициент 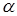 определяется из критериального уравнения для числа Нуссельта
определяется из критериального уравнения для числа Нуссельта 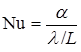 , характеризующего повышение интенсивности передачи тепла конвекцией по сравнению с теплопроводностью газа:
, характеризующего повышение интенсивности передачи тепла конвекцией по сравнению с теплопроводностью газа:
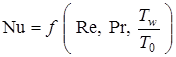 ,
,
где 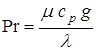 – число Прандтля.
– число Прандтля.
Каждый критерий определяет те или иные свойства потока, от которых зависит теплообмен:
· число  определяет по параметрам потока режим течения в пограничном слое и интенсивность теплопередачи конвекцией;
определяет по параметрам потока режим течения в пограничном слое и интенсивность теплопередачи конвекцией;
· число 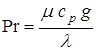 является отношением толщин динамического и теплового пограничных слоев и зависит от теплофизических характеристик (факторов): теплопроводности
является отношением толщин динамического и теплового пограничных слоев и зависит от теплофизических характеристик (факторов): теплопроводности  , теплоемкости
, теплоемкости 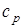 , вязкости
, вязкости 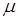 газа пограничного слоя;
газа пограничного слоя;
· температурный фактор 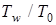 характеризует влияние изменения температуры газа в пограничном слое на теплофизические параметры газа.
характеризует влияние изменения температуры газа в пограничном слое на теплофизические параметры газа.
Здесь следует отметить, что влияние температурного фактора в условиях старта существенно в силу значительной разницы температуры газа  и температуры металлических конструкций
и температуры металлических конструкций 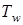 , как в начале нагревания, так и даже при плавлении металлических стенок или низкотемпературных теплозащитных покрытий.
, как в начале нагревания, так и даже при плавлении металлических стенок или низкотемпературных теплозащитных покрытий.
В критериальном уравнении влияние фактора 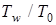 выражается либо непосредственно в виде зависимости
выражается либо непосредственно в виде зависимости  , либо через теплофизические параметры в погранслое, которые определяются с учетом падения температуры газа от
, либо через теплофизические параметры в погранслое, которые определяются с учетом падения температуры газа от  до
до 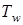 . Это падение температуры может быть учтено одним из следующих способов:
. Это падение температуры может быть учтено одним из следующих способов:
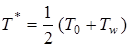
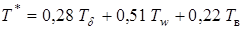 ,
,
где 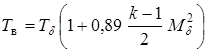 .
.
По температуре  определяются параметры:
определяются параметры: 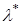 ,
, 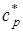 ,
, 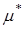 ,
, 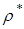 и, соответственно:
и, соответственно:  ,
, 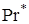 . Это является учетом влияния температурного фактора
. Это является учетом влияния температурного фактора 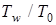 .
.
3.3.2. Схемы теплового воздействия на агрегаты пусковых устройств
Агрегаты пусковых устройств имеют сложную геометрию, поэтому при рассмотрении воздействия на них струй целесообразно выделить отдельные элементы, чтобы свести схемы воздействия к некоторым изученным случаям.
Воздействие на газоотражатель
Схема теплосилового нагружения газоотражателя показана на рис.3.28. Аналогом здесь является обтекание клина внешним потоком. Параметры струи неравномерны по сечению и по длине. При расчетах применяют осреднение по сечению струи.
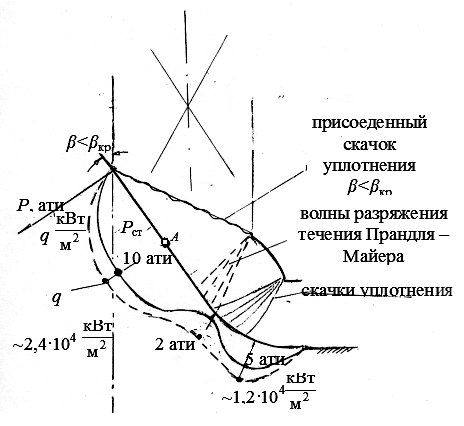
Рис.3.28. Теплосиловое нагружения газоотражателя
Вследствие неравномерности параметров по длине струи, изменение нагрузок на отражателе в зависимости от подъема ракеты имеет характер, показанный на рис.3.29, где представлено изменение теплосиловых нагрузок в точке  газоотражателя при отходе ракеты от старта (
газоотражателя при отходе ракеты от старта ( – расстояние среза сопла от вершины газоотражателя).
– расстояние среза сопла от вершины газоотражателя).
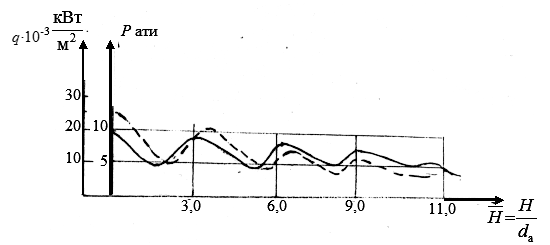
Рис.3.29. Изменение теплосиловых нагрузок в точке  газоотражателя
газоотражателя
при отходе ракеты от старта:
 – расстояние среза сопла от вершины газоотражателя
– расстояние среза сопла от вершины газоотражателя
Типовые параметры нагрузок на отражатель:
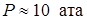 ,
, 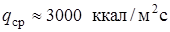 ,
, 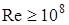 .
.
Воздействие на пусковые контейнеры
Схема теплового воздействия на стенку транспортно-пускового контейнера показана на рис.3.30. Воздействие локальное с перемещением зоны по длине трубы. Максимальное значение 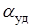 было названо "ударным". Ввиду того, что зона действия
было названо "ударным". Ввиду того, что зона действия 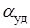 перемещается при движении ракеты в стволе, по экспериментальным данным были составлены эмпирические зависимости, позволившие проводить расчеты по осредненным параметрам.
перемещается при движении ракеты в стволе, по экспериментальным данным были составлены эмпирические зависимости, позволившие проводить расчеты по осредненным параметрам.
Рис.3.30. Тепловое воздействие на стенку
транспортно-пускового контейнера
Обтекание контейнера аналогично обтеканию пластины, так как 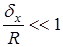 ,
, 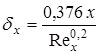 .
.
Воздействие на преграды
Схема воздействия на преграду показана на рис.3.31.
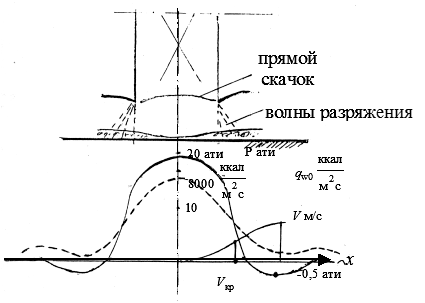
Рис.3.31. Натекание струи на преграду
Воздействие около критической точки зависит от градиента давления  .
.
Рассмотренные характерные случаи имеют аналогию с теплообменом при обтекании тел внешним потоком в отношении формирования погранслоя и в связи с этим возможно использование зависимости 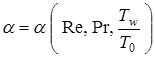 , полученной для этого общего случая (в качестве опорной).
, полученной для этого общего случая (в качестве опорной).
Однако для условий старта имеет место дополнительное воздействие на пограничный слой мощных акустических полей от излучения струй двигательной установки и от процессов взаимодействия струй с элементами пускового устройства, а, вследствие этого, – усиление интенсивности теплообмена. Это явление было обнаружено впервые при натурных испытаниях, так как оно проявляется в условиях действия больших амплитуд и низких частот пульсаций давления.
3.3.3. Зависимости для расчета теплового воздействия
Условия теплового воздействия при старте характеризуются:
· высокими значениями чисел 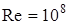 ;
;
· большим диапазоном изменения температуры в пограничном слое  , при высоких значениях
, при высоких значениях  до
до 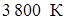 ;
;
· высоким уровнем пульсаций давления в потоке вследствие действия акустического излучения струй двигательной установки ( ).
).
Последнее существенно отличает условия теплообмена при старте от условий теплообмена при обтекании тел невозмущенным потоком.
Однако, несмотря на отмеченную специфику, закономерности изменения теплового воздействия, вызываемого изменением газодинамических и теплофизических параметров газа, аналогичны закономерностям теплообмена при обтекании поверхностей внешним потоком. Это выражается известной формулой Эккерта для коэффициента теплообмена в турбулентном потоке
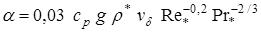 .
.
Однако значения 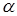 , полученные при натурных испытаниях тепловыми измерениями, оказывались выше, чем рассчитанные по приведенной формуле, в несколько раз, а иногда на порядок. Натурные данные находились в противоречии также с данными модельных испытаний.
, полученные при натурных испытаниях тепловыми измерениями, оказывались выше, чем рассчитанные по приведенной формуле, в несколько раз, а иногда на порядок. Натурные данные находились в противоречии также с данными модельных испытаний.
Исследования этого процесса позволили выявить новый, ранее неизвестный механизм воздействия на турбулентный пограничный слой акустических пульсаций большой мощности, генерируемых струями двигательной установки в каналах стартового сооружения (М.В. Сенкевич, Г.Ф. Куровский).
Исследования потребовали проведения обширного комплекса измерений параметров тепловых, газодинамических и тепловых процессов на натурных шахтных сооружениях при различных режимах пусков, обширных экспериментальных исследований на лабораторных газодинамических установках.
Обработка комплекса данных позволила установить связь коэффициента теплообмена с акустическими характеристиками. Механизм интенсификации теплового воздействия в натурной шахте было предложено учитывать введением акустического числа  , которое характеризует отношение амплитуды перемещения частиц
, которое характеризует отношение амплитуды перемещения частиц 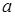 к толщине акустического пограничного слоя
к толщине акустического пограничного слоя  при колебаниях газа. Механизм усиления интенсивности теплообмена состоит в воздействии на турбулентный пограничный слой поперечного к нему перемещения частиц потока при акустических колебаниях и проявляется наиболее сильно при автоколебаниях на дискретных частотах. При этом число
при колебаниях газа. Механизм усиления интенсивности теплообмена состоит в воздействии на турбулентный пограничный слой поперечного к нему перемещения частиц потока при акустических колебаниях и проявляется наиболее сильно при автоколебаниях на дискретных частотах. При этом число  пропорционально квадрату амплитуды акустического давления и обратно пропорционально частоте колебаний. Последнее обстоятельство весьма важное, так как приводит к качественно новым результатам и зависимостям в изменении коэффициента
пропорционально квадрату амплитуды акустического давления и обратно пропорционально частоте колебаний. Последнее обстоятельство весьма важное, так как приводит к качественно новым результатам и зависимостям в изменении коэффициента 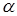 от линейного размера элементов, подвергающихся нагреву, и от масштабного фактора.
от линейного размера элементов, подвергающихся нагреву, и от масштабного фактора.
Так, вместо известной закономерности
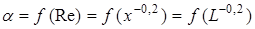 ,
,
при увеличении масштаба 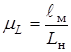 может наблюдаться рост коэффициента теплообмена с ростом масштаба вследствие уменьшения частоты
может наблюдаться рост коэффициента теплообмена с ростом масштаба вследствие уменьшения частоты 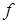 при увеличении масштаба
при увеличении масштаба  . Наоборот, с уменьшением масштаба интенсификация теплообмена уменьшается и полностью исчезает при некотором критическом значении
. Наоборот, с уменьшением масштаба интенсификация теплообмена уменьшается и полностью исчезает при некотором критическом значении  и соответствующем значении масштаба
и соответствующем значении масштаба  . Этим, в частности, объясняется то обстоятельство, что явление усиления теплообмена было обнаружено впервые на крупных натурных объектах (пусковых шахтах).
. Этим, в частности, объясняется то обстоятельство, что явление усиления теплообмена было обнаружено впервые на крупных натурных объектах (пусковых шахтах).
Для учета влияния пульсаций на теплообмен были разработаны зависимости для двух видов условий по акустическим процессам, которые имели место при старте:
· при реализации автоколебательных резонансных процессов;
· при акустических процессах с шумовым спектром.
При реализации в каналах пусковой установки автоколебательных процессов на резонансной частоте  усиление интенсивности теплообмена определяется формулой
усиление интенсивности теплообмена определяется формулой
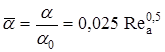 ,
,
где 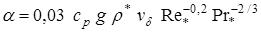 ;
;
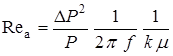 ,
,
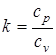 ;
; 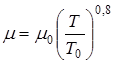 ;
;  . При
. При 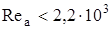
 .
.
Для воздуха 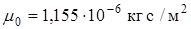 , для водяного пара
, для водяного пара 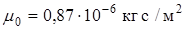 .
.
Для условий воздействия акустических колебаний с шумовым спектром в диапазоне частот 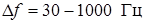 усиление теплообмена может быть определено по формуле
усиление теплообмена может быть определено по формуле
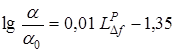 ,
,
где  – спектральная плотность в полосе
– спектральная плотность в полосе 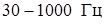 .
.
В этой формуле пороговое значение  , при котором начинается влияние акустических колебаний, составляет
, при котором начинается влияние акустических колебаний, составляет 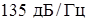 .
.
Определение зависимостей по влиянию на теплообмен акустических пульсаций с шумовым спектром было особенно актуальным для прогнозирования тепловых нагрузок на кормовую часть ракеты при минометном старте. Экспериментальные исследования этого вопроса были проведены Г.Ф. Куровским и М.В. Сенкевич на моделях достаточно крупного масштаба с измерениями газодинамических, тепловых и акустических параметров. В соответствии с данными критериальной обработки более полный учет влияния шумовых акустических пульсаций на турбулентный теплообмен осуществляется зависимостью 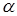 от комплекса
от комплекса 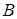 , являющегося безразмерной спектральной плотностью и учитывающего соотношения между
, являющегося безразмерной спектральной плотностью и учитывающего соотношения между  и
и  погранслоя:
погранслоя:
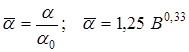 ,
,
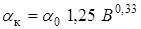 ,
,
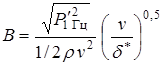 ,
,
где 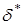 – толщина акустического погранслоя.
– толщина акустического погранслоя.
Этот комплекс можно представить через 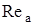 ,
,  и число
и число 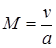 потока:
потока:
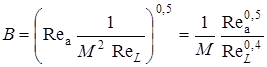 .
.
Из формулы видно, что при увеличении числа  влияние акустических пульсаций уменьшается. На основании полученных закономерностей можно рекомендовать формулы для расчета следующих случаев
влияние акустических пульсаций уменьшается. На основании полученных закономерностей можно рекомендовать формулы для расчета следующих случаев
1. Тепловой поток к пусковому контейнеру (слабо градиентное течение):
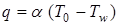 ;
; 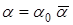 ;
; 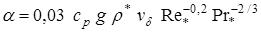 ,
,
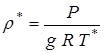 .
.
2. Обтекание отражателя (градиентное течение):
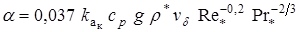 ,
,
где 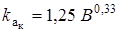 или
или 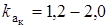 .
.
Иногда применяют формулу
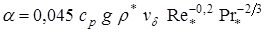 .
.
В расчете  берутся
берутся  ,
,  при
при 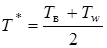 ,
,
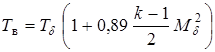 ;
;  ,
,
где 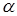 – угол наклона отражателя.
– угол наклона отражателя.
Параметры струи изменяются скачкообразно на длине струи  :
:
· в зоне первой газодинамической структуры струи  ;
;
· на длине шести структур струи 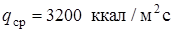 .
.
За время старта 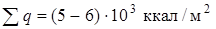 .
.
3. При натекании струи на преграду коэффициент теплоотдачи зависит от градиента скорости растекания потока
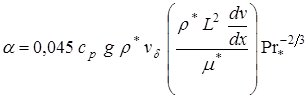 .
.
Представленные закономерности для прогнозирования конвективного турбулентного теплообмена при старте являются концентрированной формулировкой новых свойств теплообмена для реальных натурных условий воздействия струй двигательной установки большой мощности на элементы пусковых установок. Эти новые свойства (влияние акустических пульсаций, "оребрения" обтекаемых поверхностей) в ходе исследований были специально выделены на фоне классических зависимостей, установленных для исследованных течений конвективного турбулентного теплообмена.
Следует отметить, что для получения новых данных по теплообмену при старте потребовалось создание специальной комплексной системы измерений, пригодной для проведения исследований в натурных условиях. Необходимо было разработать специальные датчики теплового режима натурных конструкций и параметров высокотемпературных газов. Необходимо было проведение специальных исследований в лабораторных условиях на моделях крупного масштаба. Методика проведения таких работ рассматривается в четвертой главе.
3.3.4. Особенности конвективного теплообмена при воздействии двухфазного потока
Воздействие двухфазного потока на конструкцию пускового устройства имеет место при запыленности потока твердыми частицами или при старте ракет на ракетных двигателях твердого топлива, продукты сгорания которых имеют металлизированные частицы  или
или 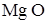 в жидкой фазе (К-фаза).
в жидкой фазе (К-фаза).
В первом случае, как правило, имеет место упругое соударение частиц со стенками, а влияние частиц на теплообмен выражается в повышении турбулизации течения в пограничном слое. Увеличение коэффициента теплопередачи будет зависеть от концентрации частиц в потоке весовой 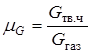 и объемной
и объемной 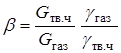 . Эти коэффициенты можно оценить по формуле Гоблица:
. Эти коэффициенты можно оценить по формуле Гоблица:
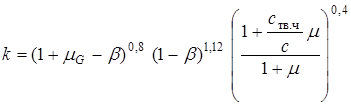 ,
,
где 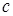 – теплоемкость.
– теплоемкость.
Плотность теплового потока может быть определена по следующей формуле:
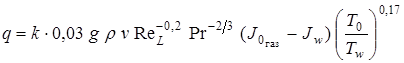 .
.
Следует отметить, что значение разности энтальпий газа 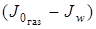 будет меньше, чем без частиц, вследствие отбора тепла от газа на нагрев частиц.
будет меньше, чем без частиц, вследствие отбора тепла от газа на нагрев частиц.
Оценки показывают, что величина теплового потока с твердыми частицами может быть выше, чем в газовом потоке, на 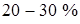 .
.
При ударе твердых частиц о стенку возможно усиление уноса материала стенки в результате механического воздействия частиц. Если стенка имеет теплозащиту, то будет иметь место аккомодация частиц на стенке (прилипание) и увеличение теплового потока.
При воздействии потока с К-фазой, помимо механизма турбулентного потока и усиления теплопередачи конвекцией, существенное влияние оказывает процесс конденсации жидких частиц на более холодной стенке. Этот новый, характерный для условий старта, эффект был исследован под руководством Ю.А. Акопяна. В этом случае тепловой поток может возрастать в несколько (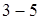 ) раз. Конденсация частиц на более холодной, чем поток, стенке, приводит к образованию твердой пленки, которая играет роль теплозащиты для металлической стенки, снижая тепловой поток за счет роста
) раз. Конденсация частиц на более холодной, чем поток, стенке, приводит к образованию твердой пленки, которая играет роль теплозащиты для металлической стенки, снижая тепловой поток за счет роста  и соответствующего уменьшения температурного или энтальпийного напора
и соответствующего уменьшения температурного или энтальпийного напора  или
или 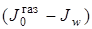 . Характер изменения теплового потока представлен на рис.3.32.
. Характер изменения теплового потока представлен на рис.3.32.
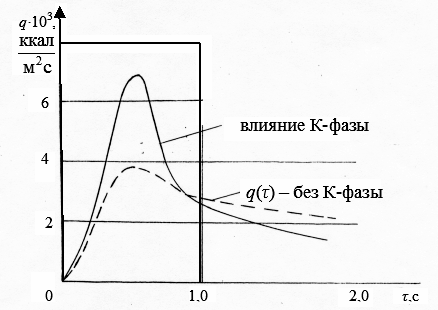
Рис.3.32. Сравнение тепловых потоков от действия
струй с К-фазой и без К-фазы
При этом интегральное количество тепла в процессе старта может быть одинаково в потоке с К-фазой или без К-фазы.
Малая теплопроводность конденсированной твердой пленки приводит к росту температуры поверхности  пленки и ее плавлению для
пленки и ее плавлению для  при температуре
при температуре 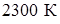 . В этом случае тепловой поток в стенку стабилизируется, а тепло газа идет на плавление верхнего слоя твердой пленки.
. В этом случае тепловой поток в стенку стабилизируется, а тепло газа идет на плавление верхнего слоя твердой пленки.
3.3.5. Лучистый теплообмен от газов двигательной установки при старте
Конвективный обмен, как было указано ранее, играет основную роль при старте. Однако, вследствие больших объемов газов, находящихся в состоянии, близком к торможению, запыленности потока, тепловой поток за счет излучения может достигать 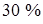 от конвективного.
от конвективного.
Газовые струи продуктов сгорания топлив ракетных двигателей излучают тепловую энергию, в основном, за счет присутствия в них водяного пара 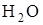 , углекислого газа
, углекислого газа  и других трехатомных компонент. Излучательная способность двухатомных газов
и других трехатомных компонент. Излучательная способность двухатомных газов 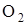 ,
, 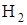 и
и  ничтожна, то есть эти газы для тепловых лучей диатермичны. Газы излучают и поглощают тепловую энергию лишь в определенных интервалах длин волн – в полосах
ничтожна, то есть эти газы для тепловых лучей диатермичны. Газы излучают и поглощают тепловую энергию лишь в определенных интервалах длин волн – в полосах 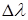 . Тепловая энергия в газе, в отличие от твердых тел, испускается и поглощается в объеме пропорционально длине прохождения луча
. Тепловая энергия в газе, в отличие от твердых тел, испускается и поглощается в объеме пропорционально длине прохождения луча 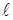 и давлению
и давлению 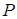 .
.
Таким образом, излучательная способность газов для какой-либо полосы длин волн 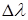 является функцией произведения
является функцией произведения 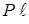 , а также температуры газов:
, а также температуры газов: 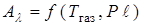 .
.
Общая лучеиспускательная способность газа равна сумме энергии лучеиспускания на всех полосах частот:
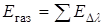 ,
,
где 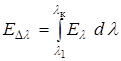 .
.
В основу практических расчетов лучеиспускания газа к стенкам может быть положен закон Стефана – Больцмана:
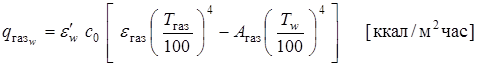 ,
,
где  – эффективная степень черноты оболочки;
– эффективная степень черноты оболочки; 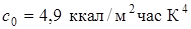 – коэффициент лучеиспускания абсолютно черного тела;
– коэффициент лучеиспускания абсолютно черного тела; 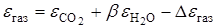 – степень черноты газа;
– степень черноты газа; 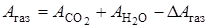 – поглощающая способность газа при температуре оболочки.
– поглощающая способность газа при температуре оболочки.
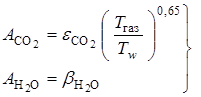
– берется по  ;
; 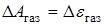 .
.
Можно принять для приближенных расчетов 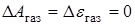 .
.
Если 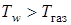 , то стенка не поглощает, а излучает энергию газу.
, то стенка не поглощает, а излучает энергию газу.
Закон Стефана – Больцмана справедлив для теплообмена между лучистой полусферой и плоскостью. Излучение объемов газов другого вида можно свести к излучению полусферы через эквивалентный радиус:
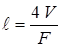 ,
,
где 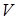 – объем газового тела;
– объем газового тела; 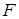 – площадь оболочки.
– площадь оболочки.
Суммарный тепловой поток будет:
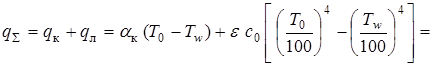
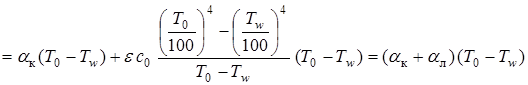 ,
,
где 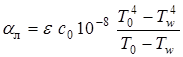 .
.
Для лучистого теплообмена в каналах шахт можно приближенно считать
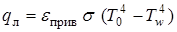 ;
;
 ;
;
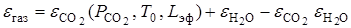 ;
;
 ,
, 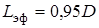 .
.
Для плоских потоков 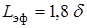 .
.
3.3.6. Нагрев стенок конструкций пусковой установки
Нагрев конструкций газоотражателей с большой толщиной стенки
Условия нагрева газоотражателей и стенок конструкции пусковых установок, подвергающихся воздействию газовых струй двигателей, характеризуются высокой температурой газа  , а также высоким значением коэффициента
, а также высоким значением коэффициента 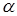 .
.
Эти параметры определяют тепловой поток в стенку 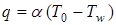 . Величины параметров во время старта изменяются вследствие удаления среза сопла и изменения параметров струи на преграде. Однако в малые отрезки времени они могут быть приняты постоянными со ступенчатым изменением за весь период старта. Такой подход является предпосылкой для графического решения нестационарной задачи теплопроводности методом Шмидта.
. Величины параметров во время старта изменяются вследствие удаления среза сопла и изменения параметров струи на преграде. Однако в малые отрезки времени они могут быть приняты постоянными со ступенчатым изменением за весь период старта. Такой подход является предпосылкой для графического решения нестационарной задачи теплопроводности методом Шмидта.
Вышеназванные условия, задающие нагрев от действия газового потока, а именно 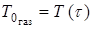 и
и 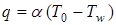 , известны в задачах о теплопроводности как условия третьего рода. Если для выделенных периодов времени
, известны в задачах о теплопроводности как условия третьего рода. Если для выделенных периодов времени 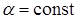 , то на стенке должно быть условие равенства в каждый момент времени теплового потока от газа к стенке и теплового потока от поверхности внутрь пластины, который определяется законом Фурье:
, то на стенке должно быть условие равенства в каждый момент времени теплового потока от газа к стенке и теплового потока от поверхности внутрь пластины, который определяется законом Фурье:
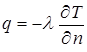 ,
,
где  – коэффициент теплопроводности стенки;
– коэффициент теплопроводности стенки;  – нормаль к поверхности.
– нормаль к поверхности.
Тогда 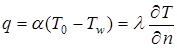 .
.
Уравнение теплопроводности в общем виде:
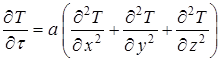 ,
,
где 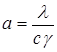 – температуропроводность стенки.
– температуропроводность стенки.
Для нагрева отражателя и контейнера, ввиду малой толщины стенки по сравнению с размером пятна от струи и больших градиентов 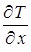 по сравнению с градиентами
по сравнению с градиентами 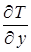 и
и 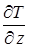 *), это уравнение может быть сведено к одномерному:
*), это уравнение может быть сведено к одномерному:
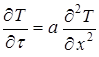 .
.
Напишем уравнение теплопроводности через конечные разности; разбив стенку толщиной  на
на  слоев толщиной
слоев толщиной 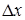 и рассматривая температуру середины слоев
и рассматривая температуру середины слоев 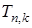 в
в 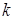 -е моменты времени с интервалом
-е моменты времени с интервалом 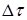 :
:
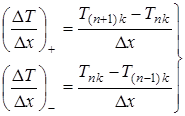 ;
;
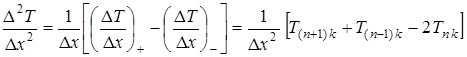 ;
;
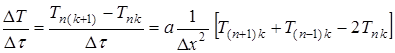 ;
;
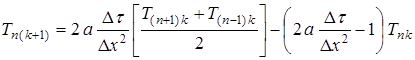 .
.
Для применения графического решения примем связь между 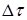 и выбранным
и выбранным 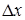 из условия:
из условия: 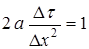 . Одновременно, равенство единице комплекса, являющегося числом Фурье
. Одновременно, равенство единице комплекса, являющегося числом Фурье 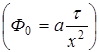 , означает возможность достижения тепловым импульсом конца слоя
, означает возможность достижения тепловым импульсом конца слоя 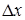 (
(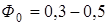 ). При этом условии уравнение теплопроводности в конечных разностях запишется как равенство температуры
). При этом условии уравнение теплопроводности в конечных разностях запишется как равенство температуры  -го слоя в
-го слоя в 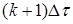 момент времени средней температуре окружающих слоев
момент времени средней температуре окружающих слоев  и
и 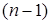 в предшествующий момент времени
в предшествующий момент времени 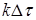 :
:
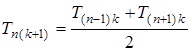 .
.
Таким образом, система трех уравнений включает:
· условие равенства тепловых потоков на поверхности пластины от газа и внутрь пластины при 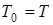
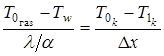 ; (3.1)
; (3.1)
· упрощенное уравнение для температуры слоев пластины
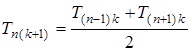 ; (3.2)
; (3.2)
· условие связи 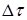 и
и 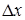
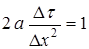 . (3.3)
. (3.3)
В системе уравнений принято (рис.3.33):
· 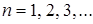 – номера выделенных слоев толщиной
– номера выделенных слоев толщиной 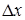 и их средних сечений;
и их средних сечений;
· 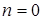 – номер выделенного фиктивного сечения на расстоянии
– номер выделенного фиктивного сечения на расстоянии 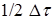 от поверхности стенки
от поверхности стенки 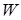 ;
;
· 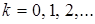 – относительное время
– относительное время  , где
, где  из уравнения (3.3).
из уравнения (3.3).

| Рис.3.33. Графическое решение нестационарного нагрева |
Воспроизводим графически условие уравнения (3.1) в момент времени  : равенство градиента температуры у стенки
: равенство градиента температуры у стенки 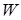 в нулевом фиктивном слое (при температуре
в нулевом фиктивном слое (при температуре  ) градиенту температуры
) градиенту температуры 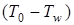 в слое толщиной
в слое толщиной 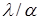 .
.
Здесь в момент времени 0 в графическом построении допускается некоторое отступление от структуры формулы (3.1) в том, что вместо градиента  берется градиент
берется градиент 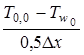 , что обеспечивает выполнение условия
, что обеспечивает выполнение условия  и условия (3.1).
и условия (3.1).
Полученное значение температуры в "нулевом" фиктивном слое в момент времени  и
и 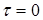 (
(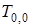 ) будет исходным для определения движения тепла внутрь пластины согласно уравнению (3.2). В последующие моменты времени градиент
) будет исходным для определения движения тепла внутрь пластины согласно уравнению (3.2). В последующие моменты времени градиент 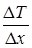 на стенке будет воспроизводиться в соответствии с формулой (3.1). Таким образом, температура
на стенке будет воспроизводиться в соответствии с формулой (3.1). Таким образом, температура 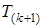 в каждом слое
в каждом слое  , включая
, включая 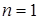 , определяется как средняя температура между соседними слоями в предшествующий момент времени
, определяется как средняя температура между соседними слоями в предшествующий момент времени 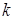 .
.
Так, для следующего момента времени 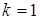 будет для
будет для 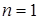 :
:
 ,
,
для слоя 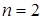
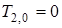 .
.
Согласно уравнению (3.1), между температурой внешнего слоя 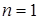 и температурой газа
и температурой газа 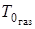 будет одинаковый градиент, что определит распределение температур в момент времени
будет одинаковый градиент, что определит распределение температур в момент времени 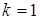 .
.
Для последующего момента времени 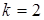 будет:
будет:
· для слоя 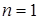
 ;
;
· 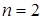
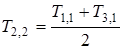 ;
;
· 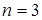
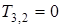 .
.
По температурам 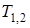 и
и 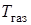 , согласно уравнению (3.1), определится температура внешнего фиктивного слоя (
, согласно уравнению (3.1), определится температура внешнего фиктивного слоя (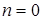 ) и температура
) и температура 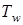 на поверхности пластины.
на поверхности пластины.
В последующих построениях для моментов времени 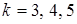 прогрев достигает последовательно слоев
прогрев достигает последовательно слоев  (рис.3.33).
(рис.3.33).
При определении температуры поверхности задней стенки принимается условие равенства нулю теплового потока от стенки к находящемуся за ней газу и равенство нулю градиента 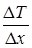 . Для графического построения температуры на задней стенке следует, аналогично построению на передней стенке, выделить фиктивный слой на расстоянии его средней линии от стенки
. Для графического построения температуры на задней стенке следует, аналогично построению на передней стенке, выделить фиктивный слой на расстоянии его средней линии от стенки  .
.
При изменении условий нагрева по 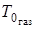 и
и 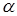 точка
точка 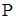 для расчета нагрева в последующие времена
для расчета нагрева в последующие времена 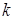 соответственно сдвигается и проводится графическое построение согласно вышеприведенному.
соответственно сдвигается и проводится графическое построение согласно вышеприведенному.
Пример 3.4.
Подготовка данных для графического решения.
Задано:  ,
,  , сталь
, сталь 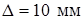 ,
,
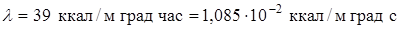 ,
,
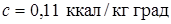 ,
, 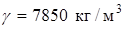 .
.
Определяем:
 ,
, 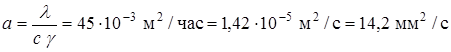 .
.
Если  ,
,  ,
,  .
.
Нагрев тонкостенных конструкций
Тонкостенные конструкции из теплопроводных материалов (алюминий – 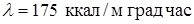 , сталь –
, сталь – 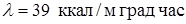 ) при высокой интенсивности теплопередачи
) при высокой интенсивности теплопередачи 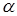 , когда критерий Био
, когда критерий Био 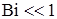
 , не имеют существенного перепада температур по толщине и им можно пренебречь при расчете нагрева конструкции по времени.
, не имеют существенного перепада температур по толщине и им можно пренебречь при расчете нагрева конструкции по времени.
Такой конструкцией может быть тонкостенная труба из алюминия или стали, из которых изготовлен контейнер для транспортировки и пуска ракеты (рис.3.34). Контейнер при установке в пусковую шахту подвергается двустороннему нагреву со стороны газов, истекающих из сопел двигательной установки и движущихся по зазору между стенками шахты и транспортно-пусковым контейнером. Изменение температуры стенки контейнера во времени можно рассчитать по приближенной формуле
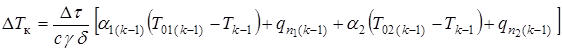 ;
;
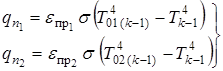 ,
,
где  – постоянная Стефана–Больцмана;
– постоянная Стефана–Больцмана;
 ,
,
 ,
, 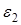 – степень черноты поверхностей.
– степень черноты поверхностей.
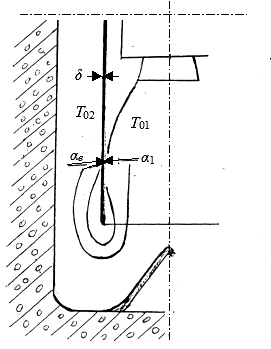
Рис.3.34. Схема теплового воздействия на стенки
транспортно-пускового контейнера
3.3.7. Приближенная оценка тепловой нагрузки на отражатель и унос материала с его поверхности, рекомендации по выбору материала, применение теплозащитных покрытий
Тепловая нагрузка на отражатель определяется интегралом теплового потока по времени. Для упрощения оценки тепловой нагрузки на отражатель заменим определенную в натурных условиях кривую  ступенчатым изменением
ступенчатым изменением 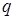 , чтобы были одинаковыми интегральные тепловые нагрузки (рис.3.35):
, чтобы были одинаковыми интегральные тепловые нагрузки (рис.3.35):
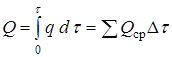 .
.
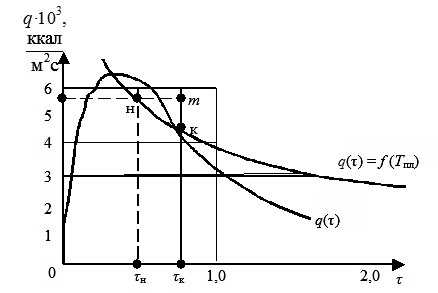
Рис.3.35. Оценка уноса стали от воздействия теплового потока 
Определим температуру 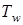 стенки при заданном тепловом потоке по приближенной формуле прогрева полубесконечного тела:
стенки при заданном тепловом потоке по приближенной формуле прогрева полубесконечного тела:
 ,
, 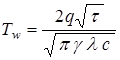 при
при 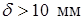 ,
,
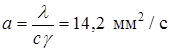 .
.
Определим время начала плавления стального газоотражателя  при
при 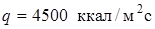 :
:
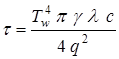 .
.
Для стали
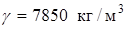 ,
, 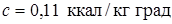 ,
, 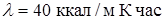 .
.
Тогда при 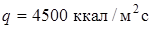 и
и 
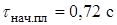 .
.
При достижении 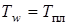 начинается унос металла. Количество тепла, расходуемого на унос металла, можно принять приближенно как избыточное интегральное количество тепла над кривой
начинается унос металла. Количество тепла, расходуемого на унос металла, можно принять приближенно как избыточное интегральное количество тепла над кривой 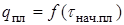 от начала плавления до снижения теплового потока ниже значения
от начала плавления до снижения теплового потока ниже значения 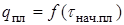 в момент
в момент 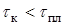 .
.
Пример 3.5.
Определим координаты кривой 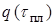 для стальной пластины (см. таблицу 3.4).
для стальной пластины (см. таблицу 3.4).
Таблица 3.4
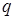 , , 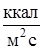
| ||||||||
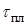 ,
с ,
с
| 0,4 | 0,481 | 0,6 | 0,73 | 0,92 | 1,18 | 1,65 | 2,31 |
Тогда можно определить избыточную теплоту, уходящую на плавление материала:
 ,
,
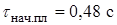 ,
, 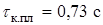 .
.
Унос материала отражателя можно определить через теплоту плавления 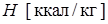 по формуле
по формуле
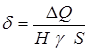 ,
,
где 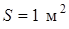 ,
, 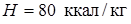 .
.
В рассматриваемом примере 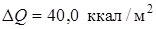 ,
,
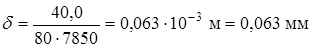 .
.
Работа некоторых материалов при одинаковых 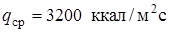 приведена в таблице 3.5 и на рис.3.36.
приведена в таблице 3.5 и на рис.3.36.

Рис.3.36. Сравнение температур поверхности нагрева различных
материалов при 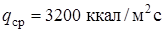
Таблица 3.5
| Материал | 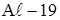
| 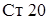
| 1Х18Н9Т | Бетон |
| Начало плавления, с | 0,52 | 0,9 | 0,8 | 0,1 |
| Длительность плавления, с | 0,68 | 0,36 | 0,68 | 1,4 |
| Унос, мм | ~0,1 | 0,3 | ||
| Данные натурных измерений, мм | 0,1 |
Из рис.3.36 и данных таблицы 3.5 следует, что целесообразным является применение более теплопроводных материалов.
Работа материалов конструкций характеризуется следующим. Отражатель из стали 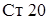 нагревается до
нагревается до  за
за 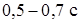 , градиент температуры
, градиент температуры 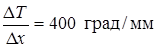 .
.
Сравним работу материалов (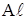 -19,
-19, 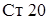 ,
, 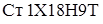 , бетон) для теплового потока
, бетон) для теплового потока 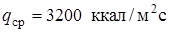 .
.
Применение теплозащитных покрытий
В случае применения теплозащитных покрытий толщина уносимого слоя может быть подсчитана из условия баланса энергии по приближенной формуле
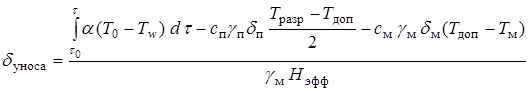 ,
,
где 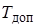 – допустимая температура металлической конструкции;
– допустимая температура металлической конструкции; 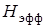 – эффективная энтальпия покрытия
– эффективная энтальпия покрытия 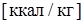 ;
; 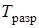 – температура разрушения покрытия (
– температура разрушения покрытия ( – легкоразрушимое покрытие).
– легкоразрушимое покрытие).
Для покрытия ПКМ-6:






