Если система линейных уравнений порядка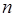 
(2.1)-(2.2), п.2.1 Лк 2
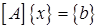
плохо обусловлена, п.2.1, (2.1а),(2.2), то это значит, что погрешности определения коэффициентов матрицы 
и правых частей 
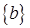, даже не очень большие, или погрешности округления при расчетах могут сильно исказить решение 
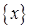. Для уменьшения погрешностей округления можно было бы произвести компьютерный расчет с двойным или даже тройным числом знаков, но при наличии погрешностей в и 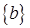это бесполезно, и нужно регуляризовать исходную задачу /3/.
Перепишем исходную систему в эквивалентной форме
(2.24)
Если коэффициенты системы или краевые части известны не точно, то решение является также приближенным, поэтому мы можем требовать только приближенного равенства (2.24). Задача становится неопределенной, и для определенности надо добавить какие-то дополнительные условия.
Таким условием может быть требование, чтобы решение как можно меньше отклонялось от некоторого вектора 
, то есть чтобы скалярное произведение векторов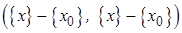 
было минимальным. Тогда регуляризованная задача формулируется так:
(2.24а)
где 
- малый положительный управляющий параметр.
Напомним, что скалярным произведением двух векторов называется сумма произведений их соответствующих элементов.
Перепишем условие (2.24а) в эквивалентной форме
(2.24б)
причем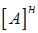 
- матрица, эрмитово сопряженная с матрицей . Варьируя 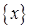в (2.24б), получим разрешающее матричное уравнение, которое является системой:
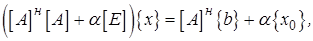(2.25)
Решив (2.25), например, методом Гаусса (или методом квадратных корней, так как матрица этой системы эрмитова), найдем регуляризованное значение 
, зависящее от малого параметра 
Относительно выбора параметра : если 
то система (2.25) переходит в исходную систему (2.1), которая плохо обусловлена apriori. Ежели велико, то регуляризованная система (2.25) будет обусловлена хорошо благодаря наличию в левой части хорошо обусловленной матрицы 
; но сама система (2.25) будет сильно отличаться от исходной, и регуляризованное решение не будет близким к истинному решению. Очевидно, оптимальным будет наименьшее значение , при котором обусловленность системы (2.25) еще удовлетворительна.
Для фактического определения оптимума вычисляют невязку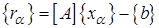 
и сравнивают ее по норме с известной погрешностью правых частей 
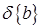и с влиянием погрешности коэффициентов матрицы 
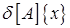. Если слишком велико, то невязка заметно больше этих погрешностей, если слишком мало – то заметно меньшие. Проводят серию расчетов с различными ; оптимальным считают тот, в котором абсолютная величина невязки приблизительно равна сумме модулей нормированных погрешностей правых частей и коэффициентов системы:
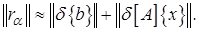(2.26)
