Векторная графика не зависит от разрешения, т.е. может быть показана в разнообразных выходных устройствах с различным разрешением без потери качества.
Достоинства векторной графики:
| Недостатки векторной графики:
|
Когда в растровых редакторах говорят о выделении объекта, то имеют в виду совокупность точек в виде области сложной формы. Процесс выделения очень часто является трудоемкой и кропотливой работой. При перемещении такого выделения появляется«дырка». В векторном же редакторе объект представляет совокупность графических примитивов и для его выделения достаточно выбрать мышкой каждый из них. А если эти примитивы были сгруппированы соответствующей командой, то достаточно «щелкнуть» один раз в любой из точек сгруппированного объекта. Перемещение выделенного объекта обнажает нижележащие элементы.
Тем не менее, существует тенденция к сближению. Большинство современных векторных редакторов способны использовать растровые картинки в качестве фона, а то и переводить в векторный формат части изображения встроенными средствами (трассировка). Причем обычно имеются средства редактирования загруженного фонового изображения хотя бы на уровне различных встроенных или устанавливаемых фильтров. 8-я версия Illustrator'a способна загружать.psd-файлы Photoshop'a и использовать каждый из полученных слоев. Кроме того, для использования тех же фильтров, может осуществляться непосредственный перевод сформированного векторного изображения в растровый формат и дальнейшее использование как нередактируемого растрового элемента. Причем, все это помимо обычно имеющихся конвертеров из векторного формата в растровый с получением соответствующего файла.
5/ Какой примитив в векторной графике представляется уравнением y=kx+b?
Прямая линия. Ей соответствует уравнение y=kx+b. Указав параметры k и b, всегда можно отобразить бесконечную прямую линию в известной системе координат, то есть для задания прямой достаточно двух параметров.
Как уже было сказано выше, основным элементом изображения в векторной графике является линия.
Объекты векторной графики хранятся в памяти в виде набора параметров. Перед выводом на экран каждого объекта программа производит вычисления координат экранных точек в изображении объекта, поэтому векторную графику иногда называют вычисляемой графикой.
Как и все объекты, линии имеют свойства. К этим свойствам относятся: форма линии, ее толщина, цвет, характер линии (сплошная, пунктирная и т.п.). Замкнутые линии имеют свойство заполнения. Внутренняя область замкнутого контура может быть заполнена цветом, текстурой, картой. Простейшая линия, если она не замкнута, имеет две вершины, которые называются узлами. Узлы тоже имеют свойства, от которых зависит, как выглядит вершина линии и как две линии сопрягаются между собой.
В основе векторной графики лежат математические представления о свойствах геометрических фигур. Рассмотрим несколько видов линий:
• Точка. На плоскости задается двумя числами (х, у), определяющими ее положение относительно начала координат.
• Прямая линия. Обычно график прямой линии описывается уравнением y=kx+b. Зная параметры k и b, всегда можно нарисовать бесконечную прямую линию в известной системе координат.
• Кривая второго порядка. К кривым второго порядка относятся параболы, гиперболы, эллипсы, окружности и другие линии, уравнения которых не содержат степеней выше второй. Прямые линии – это частный случай кривых второго порядка. Отличаются кривые второго порядка тем, что не имеют точек перегиба. Самая общая формула кривой второго порядка может выглядеть, например, так: x2+ay2+a2xy+a3x+a4y+a5=0.
• Кривая третьего порядка. Эти кривые могут иметь точку перегиба. Кривые третьего порядка хорошо соответствуют тем линиям, которые можно наблюдать в живой природе, поэтому в качестве основных объектов векторной графики используют именно такие линии. Все прямые и кривые второго порядка являются частными случаями кривых третьего порядка. В общем случае уравнение кривой третьего порядка можно записать так: x3+ay3+a2x2y+a3x y2+ a4x2+ a5y++a6xy+a7x+a8y + a9=0.
• Кривые Безье. Это частный случай отрезков кривых третьего порядка. Для их описания необходимо меньше параметров, и потому работать с ними удобнее. Метод построения кривой Безье основан на использовании пары касательных, проведенных к линии в точках ее концов. На практике эти касательные выполняют роль рычагов, с помощью которых линию изгибают так, как это необходимо. На форму линии влияет не только угол наклона касательной, но и длина ее отрезка.
Большинство векторных редакторов для изображения и хранения кривых линий используют именно кривые Безье.
6/ Какими свойствами обладает объект в графической системе AutoCAD?
Атрибуты графических примитивов. Уровни, слои, цвета и типы линий
Рисунок 3.7. Диалоговое Изменение свойств
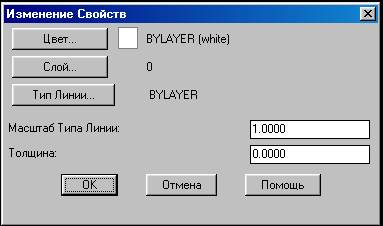
Уровень и Высота Уровень определяет значение координаты Z, а Высота определяет толщину примитива вдоль оси Z т.е. задавая высоту можно обрисовывать 3-х мерные объекты. Для работы с уровнями используется команда Уровень (Elev), уровень и высоту можно задать используя команду 'ДИАЛПРИМ ('ddmodes) Команда имеет вид: Command: elev New current elevation <20.0000>: 30 New current thickness <5.0000>:
Цвет - представляет собой число от 1 до 256, соответственно которому выбирается реальный цвет, выводимых на экран элементов чертежа(графическим и текстовым примитивам). Чаще всего, первым семи цветовым номерам присвоены стандартные значения следующим образом: 1 – красный (red); 2 - желтый (yellow); 3 - зеленый (green); 4 - голубой (cyan); 5 - синий (blue); 6 - фиолетовый (magenta); 7 - белый (white). Можно использовать как порядковые номера цветов так и их численное значение. Установка цвета может быть выполнена несколькими способами: 1). С помощью команды Формат/ Цвет выбранной из меню. При этом AutoCAD выведет на экран диалоговое окно (рис.3.1.) позволяющее установить необходимый цвет рисования. 2) С помощью команды Color введенной из командной строки.
Тип линии
Элементы чертежа можно вычерчивать различным типом линий. Тип линии - это шаблон (комбинации тире, точек и пробелов) по которому обрисовываются линии системы AutoCAD (отрезок, луч, прямая, полилиния, круг, эллипс и т.д.). Каждый тип линии имеет имя. Имя может содержать до 31 знака, и может включать буквы, цифры и специальные символы: "$" (доллар), "-" (дефис), "_" (нижняя). Тип линии можно выбрать из библиотеки стандартных типов линий, или создавать свои собственные шаблоны типов линий. Имена некоторых типов линии: continuous dash dot ___. ___. ___. ___. ___ dash - - - - - - - - - - - - - - - - - - - dot...................... Типом линий по умолчанию для всех вновь создаваемых уровней будет тип, называемый "continuous" (непрерывная), который обозначает обычную сплошную линию. Текущий тип линии м.б. изменен командами Тип Линии (linetype) и (ddltype):
Создание и настройка слоев чертежа Чертеж, создаваемый в системе AutoCAD, организован в виде набора слоев. Каждый слой содержит часть общего рисунка. Например, слой Center предназначен для проведения осевых линий, слой Frame - для рамки и основной надписи, слой Main - для детали. Для создания/настройки системы слоев используется команда меню Формат/Слой и диалоговое окно Свойства слоя и типа линии (рис. 3.5) или кнопка либо команда layer, вводимая с командной стоки.
Источник: http://life-prog.ru/view_autocad.php?id=10
Линии обладают тремя основными свойствами:
1. Цвет линий;
2. тип линий;
3. толщина линий.
7/ Масштабирование графических изображений в графической системе АutоСАD.
Масштабирование
 Рис. 4
| 1) Выделяем вставленное изображение, кликнув мышью по его границе. Вокруг него должна появиться пунктирная рамка и в углах - синие квадратики (рис. 4). Если не выделить объект до вызова команды Scale (Масштаб), то при ее выполнении первым в командной строке появится сообщение Select objects: (Выберете объекты:) Выбор выделенных объектов подтверждается нажатием Enter или правой кнопки мыши. |
 Рис. 5. Иконка команды Scale
| 2) Выполняем команду Scale (Масштаб). Удобней это сделать или нажав соответствующую иконку (рис. 5) на панели инструментов Modify (Редактирование), или набрав Scale (Масштаб) в командной строке. 3) В командной строке появится Specify base point: (Базовая точка:) Щелчком мыши указываем любую точку в рабочей области (например, один из углов рисунка) |
 Рис. 6. Задание опорного отрезка
| 4) На появившийся в командной строке запрос Specify scale factor or [Reference]: (Масштабный коэффициент или [опорный отрезок]:) отвечаем R. 5) В командной строке появится сообщение Specify reference length <1>: (Длина опорного отрезка <1>:) Указав две точки, необходимо задать отрезок, длина которого известна. Для уменьшения неизбежной относительной погрешности опорный размер следует выбирать как можно бОльшим. В нашем случае - это длина выстрела, которую удобно задать по размерной линии (точки 1 и 2 на рис. 6),. 6) В командной строке появится Specify new length: (Длина опорного отрезка:) Указываем длину в миллиметрах. В нашем примере - 262. После нажатия Enter рисунок смасштабируется. |
8/ Аффинные преобразования на плоскости. Свойства аффинных преобразований.
Преобразование плоскости называется аффинным, если оно взаимно однозначно и образом любой прямой является прямая. Преобразование называется взаимно однозначным, если оно разные точки переводит в разные, и в каждую точку переходит какая-то точка.
Частным случаем аффинных преобразований являются просто движения (без какого-либо сжатия или растяжения). Движения — это параллельные переносы, повороты, различные симметрии и их комбинации.
Другой важный случай аффинных преобразований — это растяжения и сжатия относительно прямой.
Свойства
· При аффинном преобразовании прямая переходит в прямую.
· Если размерность пространства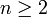 
[ источник не указан 103 дня ], то любое преобразование пространства (то есть биекцияпространства на себя), которое переводит прямые в прямые, является аффинным. Это определение используется в аксиоматическом построении аффинной геометрии
· Аффинные преобразования образуют группу относительно композиции.
· Любые три точки, не лежащие на одной прямой и их образы соответственно (не лежащие на одной прямой) однозначно задают аффинное преобразование плоскости.
· Примеры
· Частным случаем аффинных преобразований являются движения и преобразования подобия.
Типы аффинных преобразований
· Эквиаффинное преобразование — аффинное преобразование, сохраняющее площадь (также, сохраняется аффинная длина).
· Центроаффинное преобразование — аффинное преобразование, сохраняющее начало координат.
9/ Сравните построение отрезка в АutоСАD и в Си –программе.
Autocad позволяет создавать разнообразные графические объекты разной степени сложности. В этой статье мы поговорим о базовом объекте Autocad – отрезке прямой. Также, нужно отметить, что некоторые действия с графикой удобнее производить в векторном редакторе CorelDRAW (здесь можно скачать бесплатно CorelDRAW Graphics Suite 15 SP3).
Отрезки могут быть одиночными или выглядеть как ломаная линия, но при этом каждый из них является отдельным объектом. Построение отрезка выполняется заданием координат его конечных точек.
Рассмотрим пример. Выбираем инструмент Line (Линия) на ленте – горячая клавиша L. В командной строке появляется подсказка Specify first point (Укажите первую точку). Можно ввести точные координаты в командную строку, либо щелкнуть в нужном месте рабочей области. В командной строке появилось сообщение Specify next point or (Undo) (Укажите следующую точку или отмените). Выбираем следующую точку. Обратите внимание, что при этом между начальной точкой и указателем отображается предварительная линия, показывающая, как пройдет результирующий отрезок. Указывается также и угол между прямой и горизонталью. Щелкаем кнопкой мыши в нужной точке, чтобы построить отрезок. Программа предлагает построить еще один отрезок, начинающийся в конечной точке предыдущего. Теперь введем координаты конца отрезка с клавиатуры через запятую. Нажимаем клавишу Enter. Чтобы завершить выполнение команды Line (Линия), еще раз нажимаем клавишу Enter. Таким образом, мы построили два отрезка, имеющих одну общую точку.
Команда Line (Линия) может повторяться автоматически и использовать конечную точку одного отрезка в качестве начальной для следующего. Если, выбрав инструмент Line (Линия), вместо указания начальной точки нажать клавишу Enter, Autocad автоматически примет за начало нового отрезка конечную точку предыдущего. Таким способом обеспечивается легкость конструирования ломаной линии. Продолжаем создавать отрезки. В любой момент можно удалить последний отрезок и продолжить конструирование с конца предыдущего. Для этого щелкаем правой кнопкой мыши и в появившемся контекстном меню выполняем команду Undo (Назад). Если создаваемые отрезки должны образовать многоугольник, можно автоматически соединить первую и последнюю точки. Для этого опять вызываем контекстное меню и выполняем команду Close (Закрыть). Обратите внимание, что в качестве первой точки была выбрана первая точка, отмеченная при выполнении текущей команды Line (Линия)
Итак, в этой статье мы научились создавать отрезки прямой и рисовать ломаные линии. О конструировании других объектов в Autocad будет рассказано в следующих статьях.
В си можно реализовать построение алгоритма по 3м алгоритмам:
Список алгоритмов рисования отрезков
· Алгоритм DDA-линии — простой алгоритм, использующий вещественную арифметику.
· Алгоритм Брезенхэма — оптимизированный алгоритм, использующий целочисленную арифметику и только операции сложения и вычитания.
· Алгоритм Ву — модифицированный алгоритм Брезенхэма, обеспечивающий сглаживание.
Либо воспользовавшись библиотекой:
Библиотека Direct3D имеет в своем составе средства для построения связных отрезков, которые кроме всего прочего имеют толщину и стиль. Для вывода подобных примитивов (линий) предусмотрен интерфейс ID3DXLine.
Алгоритм DDA-линии:
Алгоритм DDA-линии растеризует отрезок прямой между двумя заданными точками, используя вычисления с вещественными числами. Аббревиатура DDA в названии этого алгоритма машинной графики происходит от англ. Digital Differential Analyzer (цифровой дифференциальный анализатор) — вычислительное устройство, применявшееся ранее для генерации векторов...
Целочисленный алгоритм DDA-линии
Основным недостатком алгоритма, приведенного выше является работа с числами в формате плавающей точкой. Этого можно избежать, используя арифметику с фиксированной точкой (см. Числа с фиксированной точкой).
Модифицированный алгоритм выглядит следующим образом:
#include "fixed.h"
#define roundf(x) floor(x + 0.5f)
void line_DDA_fixed(HDC hdc, float x1, float y1, float x2, float y2)
{
// (1) Целочисленные значения координат начала и конца отрезка,
// округленные до ближайшего целого
int iX1 = roundf(x1);
int iY1 = roundf(y1);
int iX2 = roundf(x2);
int iY2 = roundf(y2);
// (2) Длина и высота линии
int deltaX = abs(iX1 - iX2);
int deltaY = abs(iY1 - iY2);
// (3) Считаем минимальное количество итераций, необходимое
// для отрисовки отрезка. Выбирая максимум из длины и высоты
// линии, обеспечиваем связность линии
int length = max(deltaX, deltaY);
// особый случай, на экране закрашивается ровно один пиксел
if (length == 0)
{
SetPixel(hdc, iX1, iY1, 0);
return;
}
// (4) Вычисляем приращения на каждом шаге по осям абсцисс и ординат
fixed dX = frac_to_fixed(x2 - x1, length);
fixed dY = frac_to_fixed(y2 - y1, length);
// (5) Начальные значения
fixed x = float_to_fixed(x1);
fixed y = float_to_fixed(y1);
// Основной цикл
length++;
while (length--)
{
SetPixel(hdc, round_fixed(x), round_fixed(y), 0);
x += dX;
y += dY;
}
}
алгоритм Брезенхэма:
Алгоритм Брезенхе́ма (англ. Bresenham's line algorithm) — это алгоритм, определяющий, какие точки двумерного растра нужно закрасить, чтобы получить близкое приближение прямой линии между двумя заданными точками. Это один из старейших алгоритмов в машинной графике — он был разработан Джеком Е. Брезенхэмом (Jack E. Bresenham) в компанииIBM в 1962 году.
Реализация на C++
· Примечание: Описанный выше алгоритм не рисует вертикальных и горизонтальных линий.
Алгоритм Ву — это алгоритм разложения отрезка в растр со сглаживанием. Был предложен У Сяолинем (Xiaolin Wu, отсюда устоявшееся в русском языке название алгоритма) в статье, опубликованной журналом Computer Graphics в июле 1991 года. Алгоритм сочетает высококачественное устранение ступенчатости и скорость, близкую к скорости алгоритма Брезенхема без сглаживания.
10/ Простейшие аффинные преобразования на плоскости. Приведите математические формулы.
Аффинное преобразование и его матричное представление
Тема этого выпуска задание аффинного преобразования в матричной форме. Эта тема, по сути, является обобщением всего, что было сказано ранее.
Определение. Преобразование плоскости называется аффинным, если
- оно взаимно однозначно;
- образом любой прямой является прямая.
Преобразование называется взаимно однозначным, если
- разные точки переходят в разные;
- в каждую точку переходит какая-то точка.
Прим. Более подробно про аффинные преобразования можно посмотреть на ru.wikibooks.org
Однородные координаты
Если рассмотреть параллельный перенос, то оказывается, что для его задания матрицы 2x2 уже недостаточно. Но его можно задать с помощью матрицы размера 3x3. Появляется вопрос, откуда взять третью координату у двумерной точки?
Определение. Однородные координаты — координаты, обладающие тем свойством, что определяемый ими объект не меняется при умножении всех координат на одно и то же число.
Однородными координатами вектора (х, у) является тройка чисел (x', y', h), где х = х' / h, у = y'/h, а h — некоторое вещественное число (случай, когда h = 0 является особым).
Прим. Данные координаты не позволяют однозначно задать точку плоскости. Например, (1, 1, 1) и (2, 2, 2) задают одну и ту же точку (1, 1). Предлагается взять набор (x, y, 1), который будет описывать все точки плоскости.
Матрица преобразования для однородных координат имеет размер 3х3. Рассмотрим некоторые преобразования в однородных координатах.
Сжатие/растяжение
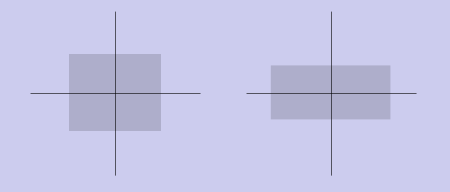
Это преобразование умножает соответствующие координаты точек на коэффициенты масштабирования по осям: (x, y) -> (ax *x, ay * y). Матрица преобразования запишется следующим образом:
[ ax 0 0 ]
[ 0 ay 0 ]
[ 0 0 1 ]
Где ax – растяжение по оси x,
ay – растяжение по оси y.
Прим. Можно заметить, что при отрицательных значениях коэффициентов сжатия/растяжения происходит отражение относительно соответствующих осей. Этот случай можно включить в данное преобразование, а можно вынести в отдельное, сказав, что коэффициенты масштабирования принимают только положительные значения.
Поворот
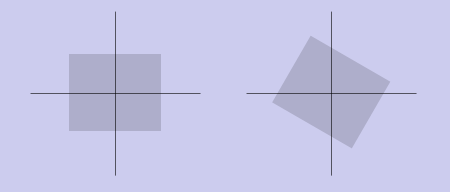
Матрица поворота 2x2 была подробно разобрана ранее. Теперь она дополняется строкой и столбцом:
[ cos(phi) sin(phi) 0 ]
[ -sin(phi) cos(phi) 0 ]
[ 0 0 1 ]
Прим. При угле phi = п эта матрица задает центральную симметрию относительно начала координат, которая является частным случаем поворота. Можно заметить, что такую симметрию можно задать с помощью преобразования сжатия/растяжения (допуская отрицательные коэффициенты масштабирования).
Параллельный перенос
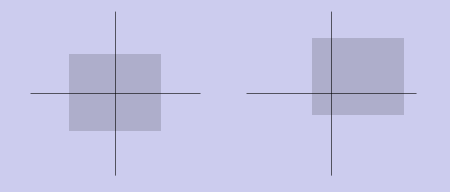
Исходный вектор (x, y) переходит в (x + tx, y + ty). Матрица преобразования запишется следующим образом:
[ 1 0 0 ]
[ 0 1 0 ]
[ tx ty 1 ]
Отражение
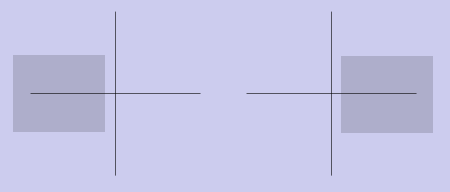
Как говорилось в примечании к преобразованию сжатия/растяжения, отражения получаются следующим образом:
[ -1 0 0 ]
[ 0 1 0 ]
[ 0 0 1 ]
отражение относительно оси x
[ 1 0 0 ]
[ 0 -1 0 ]
[ 0 0 1 ]
отражение относительно оси y
Общий вид аффинного преобразования
Матрица 3x3, последний столбец которой равен (0 0 1)T, задает аффинное преобразование плоскости:
[ * * 0 ]
[ * * 0 ]
[ * * 1 ]
По одному из свойств, аффинное преобразование можно записать в виде:
f(x) = x * R + t,
где R – обратимая матрица 2x2, а t – произвольный вектор. В однородных координатах это запишется следующим образом:
[ R1,1 R1,2 0 ]
[ R2,1 R2,2 0 ]
[ tx ty 1 ]
Если умножить вектор-строку на эту матрицу получаем результат преобразования:
[ x y 1 ] * [ R1,1 R1,2 0 ]
[ R2,1 R2,2 0 ]
[ tx ty 1 ]
=
[ x’ y’ 1 ] + [ tx ty 1 ]
При этом [ x’ y’ ] = R * [ x y ]
Прим. Любопытный читатель уже задал себе вопрос: в чем смысл определителя матрицы R? При аффинном преобразовании площади всех фигур изменяются в |R|. (Можно строго доказать это с точки зрения математики, но здесь этот факт приводится без доказательства.)
Т.о. аффинное преобразование представляется в виде композиции некоторого преобразования, задаваемого матрицей R, и параллельного переноса. Разберем более подробно природу этой матрицы и возможности, которые она нам дает.
Матрица R определяет новый базис плоскости. Т.е. вектор (1, 0) переходит в (R1,1, R1,2), вектор (0, 1) переходит в (R2,1,R2,2). Новый базис это строки матрицы R.
Пример.
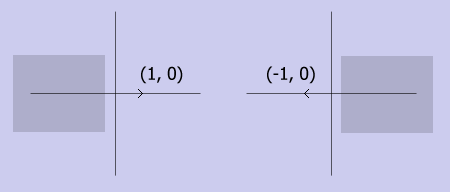
При отражении относительно оси y, базисный вектор по оси ординат сохраняется, а по оси абсцисс переходит в (-1, 0). Т.о. матрица R будет выглядеть следующим образом:
[ -1 0 ]
[ 0 1 ]
Теперь становится ясно, что кроме вышеперечисленных преобразований, с помощью аффинного преобразования можно получить скос:
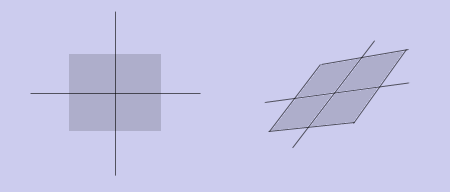
Выше приведены базовые сведения о таком мощном инструменте, как аффинное преобразование. Остается много вопросов: какой подкласс аффинных преобразований сохраняет углы между прямыми? Как можно представить аффинное преобразование в виде композиции нескольких подклассов? Как задавать более сложные преобразования, например, осевая симметрия относительно произвольной прямой?
Ответы на эти вопросы и более детальное рассмотрение аффинного преобразования будут приведены отдельно, в качестве раздела курса теоретической геометрии.
Остановимся на практической реализации аффинного преобразования в виде демонстрационной программы. К возможностям приложения, демонстрирующего поворот плоскости мышью, добавляются функции параллельного переноса при нажатой клавишеCTRL.
Т.к. эта статья является завершающей в данном разделе, код демонстрационного приложения должен быть соответствующим. Давайте попробуем разобраться, какие блоки нужны в графическом приложении, параллельно рассматривая, как они реализованы в данной программе:
· блок, в котором происходит создание окна и обрабатываются сообщения операционной системы, реализован в файлemain.cpp
· графический движок, выполняющий отрисовку изображения, класс Engine
· прослойка, необходимая для преобразования логических координат в оконные и обратно, класс Viewport
· объект, отвечающий за реакцию на действия пользователя, класс Action
В приведенном примере реализованы эти функциональные блоки, с подробными комментариями.
11 Понятие цвета в компьютерной графике. Управление цветом в Си программах.
При субъективном описании такого цвета обычно используют три величины: цветовой тон, насыщенность и светлота. Цветовой тон позволяет различать цвета, такие как красный, зеленый, желтый и т. д. Насыщенность характеризует чистоту, т. е. степень ослабления (разбавления) данного цвета белым светом, и позволяет отличать розовый цвет от красного, изумрудный от ярко-зеленого и т. д. Другими словами, по насыщенности судят о том, насколько мягким или резким кажется цвет. Светлота отражает представление об интенсивности, как о факторе, не зависящем от цветового тона и насыщенности.
Для передачи и хранения цвета в компьютерной графике используются различные формы его представления. В общем случае цвет представляет собой набор чисел, координат в некоторой цветовой системе.
Стандартные способы хранения и обработки цвета в компьютере обусловлены свойствами человеческого зрения. Наиболее распространены системы RGB для дисплеев и CMYK для работы в типографском деле.
Иногда используется система с большим, чем три, числом компонент. Кодируется спектр отражения или испускания источника, что позволяет более точно описать физические свойства цвета. Такие схемы используются в фотореалистичном трёхмерном рендеринге.
1. Цвет как свойство графических объектов в АutоСАD.
2. Построение окружности в Си- программе и в графической системе АutоСАD. Сравните методы.
- Понятие примитивов в векторной графике. Состав примитивов и их свойства в среде АutоСАD.
- Основные свойства и особенности полилиний в графической системе AutoCAD.
- Геометрические модели 3d составных объектов.
- Что такое кривые Безье в векторной графике?
- Чем занимается геометрическое моделирование?
