Системы регулирования по каскадной схеме

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

по разработке систем управления промышленными технологическими процессами, заданными типовыми моделями

для подготовки к государственному экзамену по направлению

«Автоматизация и компьютерно – интегрированные технологии

Утверждены на заседании

кафедры АТП

7.11.2007, протокол №4

Одесса, 2008

СОДЕРЖАНИЕ

1. Одноконтурные системы регулирования 3

2. Системы регулирования по инвариантной схеме 4

3. Системы регулирования по каскадной схеме 6

4. Системы многомерного управления. Общие сведения 8

5. Синтез оптимального цифрового П-регулятора для

одномерного типового объекта 9

6. Синтез системы управления для простейшего многомерного объекта 10

7. Синтез апериодического регулятора 11

8. Реализация управляющих воздействий 11

1. Одноконтурные системы регулирования

Такие системы проще всего проектируются по методике Копеловича. Параметры настройки регуляторов ПИД-семейства определяются по типовой модели процесса и принятому виду переходного процесса в соответствии с таблицей, где – перерегулирование, – время регулирования, , , .

Объект	, %	П	ПИ	ПИД

		0.30	0.60	0.80	0.50	0.95	2.40		0.40
	0.70	0.70	1.00	0.30	1.20	2.00		0.40
	0.90	1.00	1.00	0.35	1.40	1.30		0.50
		0.345	0.46	5.75		0.65	5.00		0.23
	0.71	0.70	3.00		1.10	2.00		0.37
	––	1.045	4.30		1.365	1.60		0.51
		6Т	4Т

Параметры настройки определяются, если . Если , можно считать и определять настройки для безынерционного объекта, основываясь непосредственно на свойства типовых звеньев. Статическую ошибку по заданию в П-регуляторе можно убрать, введя компенсатор задания, т.е. реализовав закон в виде , .

Уравнения регуляторов в цифровой форме имеют вид:

Закон	Выражение в дискретном времени	Пересчет коэффициентов
П
ПИ
ПИД

2. Системы регулирования по инвариантной схеме

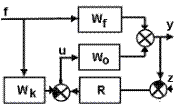
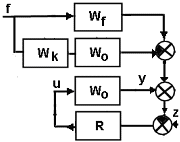Системы проектируются на основе структурной схемы, изображенной на рисунке. Для разработки системы, обеспечивающей независимость выхода объекта y от возмущения f, возмущение необходимо измерить и пропустить через компенсатор с передаточной функцией . Используя известные правила преобразования, получим вторую структурную схему, откуда видно, что условием инвариантности является , т.е. .

Для типовых моделей, описываемых передаточными функциями инерционного (объект обозначен индексом ¹) или интегрального (объект обозначен индексом ²) звена первого порядка с запаздыванием:

;

компенсатор может быть описан передаточной функцией

Ясно, что компенсатор реализуем, если

Рассмотрим вначале реализацию компенсатора . Представив в виде , можем записать. . Тогда, перейдя к дифференциальным уравнениям, ; , получим ; ; ; . Выбрав период дискретизации таким образом, чтобы делилось на нацело, (если , то ), перейдём к записи компенсатора в дискретном времени ; , где ; . Для упрощения реализации компенсатора перейдём к матричной записи. Нарисуем структурную схему

и по ней сразу запишем модель компенсатора в матричном виде

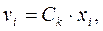
где

Предположив, что для стабилизации выбран ПИ-регулятор, программу реализации регулятора инвариантной системы с компенсатором измеряемых возмущений в случае пропорционального исполнительного механизма (пневматический, гидравлический, шаговый и т.д.) можно записать в виде

;

output(port,u–v);

Рассчитывая компенсатор для интегрального звена, мы можем записать систему в дискретном времени , , которой соответствует структурная схема

и матричная запись

Выбрав для стабилизации П-регулятор, можем записать программу (для пропорционального ИМ)

; ; ;

Системы регулирования по каскадной схеме

Системы проектируются на основе структурной схемы, изображенной на рисунке. Регулятор называется стабилизирующим, а регулятор - корректирующим. Вид закона регулирования для регуляторов и и параметры их настройки можно выбирать в соответствии с формулами, указанными в таблице

Вид каскада	Условия использования	Стабилизирующий регулятор R₁	Корректирующий регулятор R₂
П-ПИ
ПИ-ПИ
ПИ-ПИД