Пространство вообще является трехмерным и, конечно, система координат должна включать в себя три перпендикулярных оси. Одна из этих осей – вертикальная – является осью высот. Измерение и порядок отсчета высот будут рассмотрены ниже. В данном вопросе речь будет идти о горизонтальных координатах, характеризующих местоположение точки (МС, ППМ и т.п.) на земной поверхности.
1.Географическая система координат.
Системы координат, относящиеся к этому виду (нормальные сферические, геодезические и астрономические), уже рассмотрены выше. Достоинством таких систем является то, что они являются едиными для всей Земли: координаты точки однозначно определяют ее местоположение. Но они неудобны для определения местоположения ВС относительно заданной траектории. Например, зная широту и долготу, невозможно сразу сказать, находится ВС на ЛЗП или уклонилось от нее.
2.Ортодромические системы координат.
Ортодромические системы (grid systems) являются обобщающим случаем сферических координат. Вместо «настоящих» меридианов и параллелей, как в географических системах, используются меридианы и параллели условные, наиболее удобно расположенные относительно маршрута полета.
В ортодромических системах осями являются две ортодромии, перпендикулярные друг другу в начале системы координат. В зависимости от того, как направлены эти оси и где расположено начало системы координат, различают две их группы.
а) Главноортодромические.
Начало обычно размещается в ИПМ, а одну из осей, называемую главной ортодромией, направляют вдоль маршрута. Например, так, чтобы она проходила и через КПМ, либо вблизи всех ППМ. Главная ортодромия является экватором такой условной сферической системы координат. Вторая ось направляется вправо от направления полета.
Координаты могут быть выражены как в линейной мере (в километрах), так и в угловой мере, аналогично широте и долготе.

Рис. 6.1. Главноортодромическая система координат.
Преимущество главноортодромической системы состоит в том, что она используется одна на весь маршрут. Можно заранее рассчитать в этой системе координаты ППМ и близко расположенных радиомаяков, определять МС. Недостаток же ее заключается в том, что по значениям координат, например Х и У, невозможно судить непосредственно о расположении ВС относительно ЛЗП. Даже при точном следовании по маршруту обе координаты будут изменяться, поскольку маршрут имеет изломы и участки маршрута, как правило, не совпадают ни с одной из осей.
Вместе с тем, такие системы координат применяются в пилотажно-навигационных комплексах некоторых типов ВС. Система координат такого типа может использоваться и при внемаршрутных полетах, когда полеты выполняются в ограниченном район, например, при выполнении авиационных работ. В этом случае начало системы координат располагают в одной из точек этого района (например, на аэродроме вылета), а оси направляют по меридиану и перпендикулярно к нему (по касательной к параллели).
б) Частноортодромическая система координат.
Эта система координат для каждого участка маршрута своя. Одна из осей (ось S) направляется по ЛЗП данного участка в направлении полета, а вторая ось (ось Z) – вправо от нее. В зависимости от того, где расположено начало системы координат, различаются два варианта таких систем. В первом случае начало системы координат, то есть точка, где обе координаты равны нулю, располагается в начальном ППМ данного участка маршрута, то есть в том ППМ, от которого летит ВС (рис.6.2,а).

Рис. 6.2. Два варианта частноортодромических систем координат
В этом случае координата Z совпадает с линейным боковым уклонением (ЛБУ), а координта S – с пройденным от ППМ расстоянием. ЛБУ – это расстояние от МС до ЛЗП, измеренное, разумеется по перпендикуляру к ЛЗП. Измеряется ЛБУ в километрах и считается положительным при уклонении вправо и отрицательным при уклонении влево, то есть знак ЛБУ соответствует знаку координаты Z. ЛБУ соответствует английский термин cross-track error, сокращенно обозначаемый как XTE..Пройденным расстоянием Sпр называется расстояние между ППМ, от которого летит ВС, и проекцией МС на ЛЗП, то есть основанием упомянутого выше перпендикуляра. Обратите внимание, что Sпр измеряется вдоль ЛЗП и вовсе не является длиной пути ВС от ППМ до текущего МС. Если ВС развернется в середине участка и вернется в ППМ, Sпр будет равно нулю, независимо от того, какое расстояние пролетело ВС. Такой выбор системы координат удобен для экипажа. Если он знает Z и S, то он знает, насколько ВС уклонилось от ЛЗП и насколько он удалился от ППМ. Зная длину участка маршрута, легко определить и оставшееся расстояние Sост. Очевидно, что для точного следования по ЛЗП необходимо стремиться выдерживать Z=0.
Во втором случае (рис.6.2,б) начало системы координат находится в конечном ППМ участка на котором летит ВС. Координата Z по-прежнему соответствует ЛБУ, а координата S является отрицательной и равной по абсолютной величине оставшемуся расстоянию. Это тоже удобно. При выполнении полета S, оставаясь, отрицательной, увеличивается, то есть уменьшается по абсолютной величине. Момент, когда S станет равной нулю, будет соответствовать пролету ППМ. Существуют такие автоматизированные навигационные системы, выдающие экипажу S и Z, в которых сам экипаж может выбрать, какой вариант расположения начала системы частноортодромических координат будет использоваться. Но большинство современных ВС оборудовано системами, в которых однозначно предусмотрен второй из рассмотренных вариантов.
олярная система координат
Полярные координаты объекта (самолета, радиостанции, ориентира и т.д.) определяются относительно какой-либо заранее оговоренной или подразумеваемой точки (как бы полюса этой системы координат). Этой точкой обычно бывает радиомаяк или самолет. Разумеется, нельзя говорить о полярных координатах радиомаяка относительно самого радиомаяка или о координатах самолета относительно самого себя. Поэтому, когда говорят о полярных координатах ВС, начало координат подразумевается в другой точке (обычно, радиомаяке), и наоборот, полярные координаты радиомаяка могут быть указаны относительно самолета. Координатами в полярной системе являются пеленг (bearing) и дальность (distance).

Рис. 6.3. Полярная система координат
Дальность D – расстояние от начала системы координат до объекта (точки). Различают дальность наклонную L (или НД), измеренную по прямой от радиомаяка до рассматриваемой точки (например, до ПМС), и горизонтальную D (или ГД), от радиомаяка до точки на земной поверхности под самолетом, то есть до МС. Наклонная дальность всегда больше горизонтальной, а совпадает с ней, когда рассматриваемая точка (например, самолет) находится на поверхности земли. Наклонная дальность непосредственно измеряется радионавигационными системами. Горизонтальная дальность используется для определения МС на карте.

Рис. 6.4. Наклонная и горизонтальная дальности
Пеленг (П) – угол в горизонтальной плоскости между направлением, принятым за начало отсчета и направлением на объект. Отсчитывается по часовой стрелке и измеряется от 0˚ до 360˚. Если объект находится к северу, его пеленг 0˚, если к востоку – 90˚, к югу 180˚, а к западу 270˚.
Часто вместо специфического навигационного термина «пеленг» используется общепринятое (например, в географии) слово «азимут». Это одно и то же.
ЛЕКЦИЯ № 7
Тема лекции: «Определение направлений»
План лекции
1. Определение направлений
Литература
1. Ю.Н.Сарайский, И.И.Алешков Аэронавигация. Часть1. Основы навигации и Применение геотехнических средств. Учебное пособие – Санкт-Петербург, 2010
2. В.П. Бабак та ін. Безпека авіації – К.: «Техніка» - 2004
одержание лекции.
пределение направлений.
Определение и оперирование направлениями играет в навигации очень большую роль. Пеленги, путевые углы, курсы – все это направления (directions), поэтому очень важно не только знать определения этих понятий, но и представлять их образно (наглядно), уметь оперировать ими, то есть переходить от одних направлений к другим. Целесообразно представлять себе направление не как угол в общепринятом геометрическом смысле (фигура из двух сторон и угол между ними), а как именно «направление» – некоторый луч, направленный в пространстве в какую-либо сторону и не обязательно привязанный к какой-
либо точке (началу координат).
Два направления считаются одинаковыми (совпадающими) если определяющие их лучи параллельны и направлены в одну сторону. Если лучи параллельны, но направлены в противоположные стороны, направления называют обратными (противоположными). Например. на рис. 7.1 векторы А и В имеют одинаковые направления, а А и С – противоположные. Можно также ввести условно договоренность, что некоторое направление D больше направления Е в том случае, если вектор Е для совмещения с Д нужно поворачивать по часовой стрелке. Естественно, речь идет о повороте в ту сторону, в которую этот поворот будет короче. Короче говоря, какое направление «правее», то есть «более по часовой стрелке», то и больше. Например, на том же рисунке D>E>B, C>D.
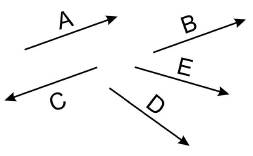
Рис. 7.1. Направления
Для количественного выражения направлений необходимо ввести какое-либо направление начала отсчета и измерять направление углом, между этим опорным направлением и данным. В навигации по традиции углы отсчитываются по часовой стрелке от опорного направления и измеряются от 0˚ до 360˚ (см. выше определение пеленга). Отметим следующие достаточно очевидные факты.
1) Два одинаковых направления имеют одинаковую числовую меру независимо от того, от какого опорного направления они отсчитываются – лишь бы от одного и того же. Так на рис.7.2 направления А и В имеют одинаковую численную меру (выражаются одинаковыми углами), если их отсчитывать как от опорного направления С1, так и от С2.
2) Если к какому либо направлению прибавить или вычесть из него 360˚, само направление от этого не изменится - куда в пространстве было направлено, туда и осталось. Изменилось лишь численное выражение этого угла. Это все равно, что измерять температуру по Цельсию или по Фаренгейту – количество градусов разное, а сама температура та же самая, ни теплее, ни холоднее.
Поскольку в полной окружности 360˚, то и направление 30˚, и 390˚, и 750˚ (750=360·2+30) – это одно и то же направление. Разумеется, нет смысла оперировать значениями, превышающими 360˚, и, если такое значение получилось в процессе расчетов, необходимо его «нормировать» – перейти в диапазон 0-360˚.

Рис.7.2. Направления начала отсчета
3) Иногда удобно для практических расчетов оперировать и отрицательными углами. В этом случае угол, отсчитываемый по часовой стрелке, считается положительным, а против часовой стрелки – отрицательным. Одно и то же направление может быть выражено как положительное (отсчитываемое по часовой стрелке), так и отрицательное (отсчитываемое против часовой стрелки), как показано на рис. 7.3. Понятно, что сумма абсолютных величин численных значений этих направлений составляет 360˚. Например, +120˚ - это то же самое, что –240˚, а 37˚=+323˚. Необходимо легко и быстро уметь переходить от положительных значений к отрицательным и обратно, поскольку это существенно упрощает выполнение многих навигационных расчетов.
3)

Рис.7.3. Положительный и отрицательный отсчет направлений
4) Численное выражение обратного (противоположного) направления отличается от исходного на 180˚. По существу безразлично, прибавить или вычесть 180˚. Просто при не очень удачном выборе одного из этих двух вариантов может получиться отрицательное значение, которое при необходимости можно выразить положительным значением, или значение, превышающее 360˚ которое затем можно «нормировать». Например, если имеется направление 146˚ и необходимо найти обратное, то получим 146+180=326.
Если бы мы вместо того, что бы прибавить 180, неудачно вычли это же число, то получили бы
146-180= –34.
Но направление –34 это то же направление, что и 326. (-34+360=326). В другом примере, если бы мы захотели получить направление, обратное направлению 250˚ и неудачно прибавили 180, то получили бы: 250+180=430.
После нормирования получим 430-360=70. Этот результат получили бы сразу, если бы не прибавили, а вычли 180. 250-180=70.
Обратите внимания: если к направлению прибавить или вычесть 180, получаем другое направление в пространстве, противоположное исходному. Полезно иметь в виду и такой очевидный факт, что если некоторое направление дважды развернуть на 180˚, получим то же самое исходное направление. Очень важно научиться быстро в уме находить обратные направления. Конечно, на первых порах при выполнении этой операции человек выполняет арифметическое действие прибавления или вычитания, то есть считает в уме. Но практика показывает, что после некоторой тренировки человек просто запоминает, какое направление какому обратному соответствует. Так зачем считать каждый раз одно и то же, если потом все равно результаты сами собой запомнятся? Не лучше ли их выучить с самого начала? Тем более, что запоминать-то надо не так и много. Ведь можно обратить внимание, что после прибавления или вычитания 180°, последняя цифра угла не изменяется: 317-180=137, 34+180=214 и т.д. Следовательно, необходимо запомнить только пары десятков градусов. 0 – 180, 10 –190, 20 – 200, ……. 160 – 340, 170 –350.
Но и из этих пар, некоторые наверняка уже запомнены: 0 – 180, 90 – 270. Таким образом, запомнить, оказывается, нужно всего 16 пар. Поэтому опытный пилот или штурман переводит направления в противоположные следующим образом.
Дано 295°. В паре с 290° состоит 110° (это уже выучено), последняя цифра не изменяется, значит обратное направление 115°. Перечисленные рекомендации позволяют существенно упростить многие навигационные расчеты. Например, необходимо вычислить сумму двух направлений: 236°+353°. «Прямой» математический расчет дает 236+353=589. Приходится нормировать: 589-360=229. Но можно сосчитать и по-другому, выразив один из углов как отрицательный (353= -7). Получим 236+(-7)=229. Результат тот же, но не пришлось оперировать большими числами.
Еще пример: 198°+264°. Прямым расчетом получаем 198+264=462=462-360=102. Это же можно сосчитать так: каждое из слагаемых развернем на 180° – сумма (результирующее направление) от этого не изменится, так как мы к ней просто прибавили (или вычли) 360, дважды развернувшись в обратную сторону. Тогда легко получим 18+84=102.
ЛЕКЦИЯ № 8
Тема лекции: «Магнитное склонение и правило учёта поправок»
План лекции
1. Магнитное склонение
2. Правило учёта поправок
Литература
1. Ю.Н.Сарайский, И.И.Алешков Аэронавигация. Часть1. Основы навигации и Применение геотехнических средств. Учебное пособие – Санкт-Петербург, 2010
2. В.П. Бабак та ін. Безпека авіації – К.: «Техніка» - 2004
одержание лекции.
агнитное склонение
В навигации в качестве начала отсчета выбирают различные направления. В географии, как и во многих других науках, азимут (пеленг) отсчитывают от северного направления географического меридиана. В навигации любой географический меридиан (дугу большого круга проходящую через полюсы) называют истинным меридианом, а измеренные от него направления истинными. Например, истинный пеленг самолета (ИПС), истинный курс (ИК) и т.д. Поэтому определение ИПС можно дать такое. Истинный пеленг самолета – это угол, заключенный между северным направлением истинного меридиана и направлением на самолет. В этом определении о «северном направлении» упоминается потому, что в любой точке (кроме полюсов) меридиан направлен как в сторону северного полюса, так и в сторону южного. Начало полярной системы координат, то
есть от какой точки берется направление на самолет, здесь не упоминается, но подразумевается в каждом конкретном случае. Так, если ИПС получен с помощью наземного радиомаяка, то подразумевается направление на самолет от этого радиомаяка.
Очень часто в навигации в качестве начала отсчета используется северное направление магнитного меридиана. Дело в том, что одним из древнейших навигационных приборов является магнитный компас, поэтому полученные с его помощью направления называются магнитными.
За северное направление магнитного меридиана в данной точке принимается направление горизонтальной составляющей вектора напряженности магнитного поля Земли в данной точке. Это направление не совпадает с направлением истинного меридиана, поскольку магнитное поле Земли неравномерно.
Магнитное склонение ΔМ – угол, заключенный между северным направлением истинного и магнитного меридианов в данной точке. Оно отсчитывается от истинного меридиана к востоку со знаком плюс, а к западу – с минусом.
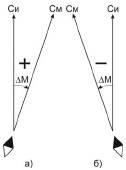
Рис. 8.1. Магнитное склонение
На английском языке для истинных величин используется прилагательное true, а для магнитных – magnetic. Например, true bearing. Магнитное склонение – magnetic variation или просто variation. В различных точках Земли ΔМ разное и может меняться от –180° до +180°. Правда, очень большие значения наблюдаются, как правило, лишь в районе магнитных и географических полюсов.
Определить величину ΔМ в любой точке можно с помощью аэронавигационных карт на которых нанесены линии, соединяющие точки с одинаковым магнитным склонением – изогоны. На аэронавигационных картах изогоны наносят пунктиром красного цвета, а на радионавигационных (маршрутных) – голубого.
Для того, чтобы узнать магнитное склонение в интересующем месте, нужно найти ближайшую к нему изогону. В районах магнитных аномалий (например, Курская магнитная аномалия) ΔМ может значительно меняться на коротких расстояниях. В этом случае на картах, предназначенных для полетов на небольших высотах, в данном районе изогоны не проводят, а просто указывают, что это район аномалии и в каком диапазоне здесь может меняться ΔМ. На высотах более 3000…5000 м аномалии уже не сказываются.

Рис. 8.2. Истинный и магнитный пеленги самолета
2. Правило учёта поправок
Если измерять одно и то же направление от истинного или магнитного меридиана, их численные выражения будут различными и отличаться на величину ΔМ. Пилот и штурман должен безошибочно уметь переходить от одной системы отсчета к другой. Из рис. 8.2 (на этом рисунке ΔМ изображено положительным) магнитный пеленг самолета (МПС) может быть найден по ИПС, и наоборот.
МПС=ИПС- ΔМ
ИПС=МПС+ ΔМ
Эти же формулы останутся справедливыми и в том случае, если ΔМ отрицательно. Разумеется, в этом случае нужно пользоваться общепринятыми правилами математики (плюс на минус дает минус, минус на минус дает плюс и т.д.). Например, ИПС=219°, ΔМ =-5°, МПС=219-(-5)=224.
Вообще, все величины, которые имеют знак (в том числе ΔМ) в навигации принято записывать со знаком, то есть плюс не пропускается. Неправильно писать ΔМ =5, а правильно ΔМ =+5. Это как бы подтверждает, что знак именно плюс, а не что его, возможно, забыли написать. В некоторых учебниках, чтобы напомнить о наличии знака у величины и необходимости его учета, эти же формулы записывают, например, так ИПС=МПС+(± ΔМ).
Возможно, такая форма записи привилась с тех времен, когда летчиков ля Красной Армии готовили из лиц с образованием семь классов. Сейчас, когда все имеют среднее образование и проходили в школе алгебру, напоминать о наличии у величины собственного знака явно излишне.
Таким образом, при переходе от МПС к ИПС магнитное склонение нужно прибавить, а при переходе от ИПС к МПС – вычесть. Разумеется, это правило справедливо и тогда, когда рассматривается не пеленг, а какое-либо другое направление – курс, путевой угол и т.п. Запомнить это правило, конечно, нетрудно, а если забыл – легко вспомнить, нарисовав что-то наподобие рис. 2.22 и выявив соотношения между направлениями, измеряемыми от истинного и магнитного меридианов. Однако дело осложняется тем, что в качестве направлений начала отсчета используются и другие направления, называемые направлениями компасного, условного, опорного меридианов и т.д. Соответственно появляются и другие разновидности поправок, кроме ΔМ, для перехода от одного меридиана к другому. И каждая из них может иметь свой знак. И здесь уже разобраться в «веере» меридианов не так и просто. Вместе с тем переходить от меридиана к меридиану необходимо быстро и безошибочно. Для этого используется так называемое «правило учета поправок в навигации». Само слово «поправок» говорит о том, что мы используем их (поправки) для того чтобы «поправить» (уточнить, скорректировать) какое-либо неточное значение (обычно, показания прибора), чтобы получить более «истинное» (правильное, точное) значение. Может оказаться необходимым внести несколько поправок и не обязательно они связаны с неточностью приборов, а могут быть вызваны просто переходом от одного начала отсчета к другому (как в случае с ΔМ). После последовательного учета поправок измеренное (приборное) значение становится все более и более правильным, или, как говорят, более «истинным». Правило учета поправок может быть сформулировано следующим образом. При переходе от приборных величин к истинным поправки прибавляются, а при переходе от истинных к приборным – вычитаются. Применительно к учету ΔМ это правило может быть применено следующим образом. Магнитный меридиан как начало отсчета, конечно, является более «приборным», чем истинный. Поэтому при переходе от магнитных величин (пеленгов, курсов и т.п.) магнитное склонение необходимо прибавлять, а при переходе от истинных к магнитным – вычитать. Разумеется, прибавлять и вычитать с учетом собственного знака ΔМ.
Сейчас, пока рассмотрена всего одна поправка (ΔМ) полезность и удобство правила учета поправок не очевидны, но по мере того, как будут появляться новые виды поправок (и не только для угловых величин) «мощь» этого правила станет явной. Одно правило заменит десятки формул, предназначенных для перехода от одних величин к другим. В англоязычных учебниках по навигации это правило приводится в следующем виде. «Variation west – magnetic best. Variation east – magnetic least». Дословно это означает: «Магнитное склонение западное – магнитный (курс, пеленг) лучше (в смысле – больше истинного). Магнитное склонение восточное – магнитный (курс, пеленг) наименьший (то есть, меньше истинного)».
ЛЕКЦИЯ № 9
Тема лекции: «Навигационные и пилотажные элементы»
План лекции
1. Навигационные элементы
2. Пилотажные элементы
Литература
1. Ю.Н.Сарайский, И.И.Алешков Аэронавигация. Часть1. Основы навигации и Применение геотехнических средств. Учебное пособие – Санкт-Петербург, 2010
2. В.П. Бабак та ін. Безпека авіації – К.: «Техніка» - 2004
одержание лекции.
авигационные элементы
Навигационные элементы. Навигационные элементы – скалярные величины, характеризующие положение и перемещение ВС в пространстве. Соответственно они разделяются на навигационные элементы положения и навигационные элементы движения. Навигационные элементы положения – это величины, которые показывают, в какой точке пространства находится ВС. Очевидно, что навигационные элементы положения это не что иное, как координаты ВС – в любой системе координат.
Навигационные элементы движения характеризуют, как перемещается ВС в пространстве. Это величины, описывающие скорость и ускорение ПМС. Правда, скорость и ускорение – величины векторные, то есть имеют модуль и направление. А ведь навигационные элементы в соответствии с приведенным определением должны являться скалярами. Однако, понятно, что вектор можно описать двумя скалярными величинами: модулем и углом, характеризующими его направление, либо компонентами (составляющими) вектора по осям координат. Сами понятия движения и покоя относительны. Человек, летящий в самолете, относительно него неподвижен, а относительно земли движется. Точно так же и движение самолета можно рассматривать относительно воздушной массы, в которой выполняется полет и на которую ВС опирается, либо относительно Земли. Скорость перемещения ВС относительно воздушной массы называется
истинной воздушной скоростью (Vи). Иногда кратко ее называют просто истинной скоростью и обозначают просто V (если из-за этого не возникнет недоразумений, поскольку существуют и другие виды воздушных скоростей). По-английски эта скорость обозначается TAS (true airspeed). Одним из навигационных элементов движения является модуль (абсолютная величина) этой скорости, который на большинстве этапов полета принято измерять в километрах в час, а при заходе на посадку – в метрах в секунду.
Другим навигационным элементом движения, связанным с этим вектором скорости, является угол, характеризующий его направление относительно меридиана. У самолетов истинная скорость направлена туда же, куда направлен вектор тяги двигателей (ведь именно из-за этой тяги самолет движется), то есть примерно по направлению продольной оси ВС. На самом деле из-за несимметричности тяги направление истинной скорости не совсем совпадает с продольной осью ВС, составляя с ней угол, называемый аэродинамическим углом сноса (в аэродинамике используется
термин «угол скольжения»). Но для самолетов этот угол на установившихся режимах полета мал и составляет доли градусов, поэтому в аэронавигации обычно не учитывается. Другое дело для вертолетов. У них истинная скорость создается не непосредственно двигателями, а горизонтальной составляющей тяги несущего винта. Она может быть направлена в принципе в любую сторону – ведь вертолет может лететь и боком, и хвостом вперед. Даже в установившемся полете по маршруту вследствие особенностей аэродинамики вертолета аэродинамический угол сноса у вертолета может достигать значительных величин – до 4-5°, а при транспортировке груза на внешней подвеске и больших значений. В полете его необходимо определить и учитывать во всех навигационных расчетах. Таким образом, можно считать, что вектор истинной воздушной скорости у самолета направлен по продольной оси самолета. Но это направление, измеренное относительно меридиана, есть не что иное, как курс самолета. Следовательно, курс является для самолета как пилотажным, так и навигационным элементом.

Рис. 9.1. Истинная воздушная скорость и магнитный курс
Перемещение самолета относительно земли характеризуется вектором полной скорости Wп. В общем случае он направлен к горизонту под углом, называемым углом наклона траектории θ (vertical path angle). Вектор полной скорости принято раскладывать на вертикальную и горизонтальную составляющие. Вертикальная составляющая называется вертикальной скоростью и обозначается Vв или Vу. Заметим, что вертикальное перемещение ВС относительно воздухи и относительно земли практически одинаково, если, конечно, самолет не попал в восходящий или нисходящий поток воздуха, что бывает не так часто.
На английском языке используются термины rate of climb (вертикальная скорость набора высоты) и rate of descent (вертикальная скорость снижения).

Рис.9.2. Полная, вертикальная и путевая скорости
Вертикальная скорость измеряется в метрах в секунду, а за рубежом иногда в футах в минуту (1 м/с = 197 ф/мин). Величина горизонтальной составляющей Wп.гор практически совпадает с величиной полной скорости, поскольку для гражданских самолетов θ обычно не превышает 5-7°. Для характеристики перемещения ВС относительно земли в горизонтальном направлении обычно используется скорость, называемая путевой скоростью. Путевая скорость W(ground speed, GS) это скорость перемещения МС по земной поверхности. Движется в пространстве самолет (ПМС), соответственно перемещается и его проекция на земную поверхность (МС). Строго говоря, путевая скорость не совпадает с горизонтальной составляющей полной скорости Wп.гор из-за кривизны Земли, поскольку МС перемещается по Земле, а ПМС – на высоте. Но разница эта для всех высот, на которых выполняются полеты в авиации, совершенно незначительна и ею можно смело пренебречь. Можно считать, что путевая скорость это и есть скорость горизонтального движения ВС относительно Земли. Направление вектора путевой скорости относительно меридиана называется фактическим путевым углом βф (ФПУ). В зависимости от выбранного меридиана можно использовать фактический магнитный путевой угол (ФМПУ), фактический истинный путевой угол (ФИПУ) и другие его виды. Измеряются путевые углы, как и курсы и пеленги, по часовой стрелке от 0 до 360є. По-английски ФПУ- это actual track angle, то есть дословно – угол фактической линии пути. На практике это выражение часто используют в сокращенном виде – actual track или просто track (TK). Таким образом, слово track, обозначающее саму линию пути, может использоваться и в значении путевого угла, характеризующего направление этой линии пути.

Рис. 9.3. Фактический путевой угол
Очевидно, что вектор путевой скорости W направлен по направлению ЛФП в данной точке (если ЛФП кривая, за ее направление принимается направление касательной к ней). Действительно, ведь за счет W место самолета и перемещается, описывая ЛФП. Поэтому ФПУ можно определить также как угол, заключенный между северным направлением меридиана и направлением ЛФП в данной точке.
илотажные элементы
Навигация и пилотирование являются процессами управления движением ВС. Для того, чтобы описывать это движение используются величины, называемые навигационными и пилотажными элементами.
Пилотажные элементы – это скалярные величины, характеризующие угловое положение ВС в пространстве Пространство трехмерно, поэтому ВС, как и любое тело, можно вращать вокруг трех перепендикулярных осей. Поэтому угловое положение ВС характеризуют три величины: крен, тангаж и курс (рис.9.4).
Крен (roll) χ – это угол между горизонтальной плоскостью и поперечной осью ВС.
Тангаж(pitch) – угол между горизонтальной плоскостью и продольной осью ВС. Если он положителен, «нос» ВС поднят вверх, а если отрицателен – вниз.

Рис. 9.4. Пилотажные элементы
Курс(heading) γ – угол в горизонтальной плоскости, заключенный между направлением, принятым за начало отсчета и проекцией на эту плоскость продольной оси ВС.
Если продольная ось ВС горизонтальна (тангаж равен нулю), то можно сказать проще, что курс – это угол, между направлением, принятым за начало отсчета и продольной осью самолета.
Измеряется курс, как и пеленг, по часовой стрелке от 0° до 360є. В качестве направления начала отсчета используется северное направление меридиана – истинного, магнитного или любого другого. К пилотажным элементам можно отнести и производные перечисленных пилотажных элементов, то есть угловые скорости изменения крена, курса и тангажа, но они нам не понадобятся.
ЛЕКЦИЯ № 10
Тема лекции: «Заданный путевой угол и условия полёта по линии заданного пути»
План лекции
1. Заданный путевой угол
2. Условия полёта по линии заданного пути
Литература
1. Ю.Н.Сарайский, И.И.Алешков Аэронавигация. Часть1. Основы навигации и Применение геотехнических средств. Учебное пособие – Санкт-Петербург, 2010
2. В.П. Бабак та ін. Безпека авіації – К.: «Техніка» - 2004
Содержание лекции
аданный путевой угол
ФПУ характеризует направление фактического перемещения ВС, куда он движется на самом деле. Но должно ВС перемещаться вдоль ЛЗП, значит по ней и должен быть направлен вектор путевой скорости. Поэтому можно ввести понятие заданного путевого угла.
Заданный путевой угол βз (ЗПУ) – угол заключенный между северным направлением меридиана и линией заданного пути. Он может отсчитываться от истинного (ЗИПУ), магнитного (ЗМПУ) меридианов или какого-либо другого направления, принятого за начало отсчета. Как и у других углов (пеленга, курса) диапазон его возможного изменения составляет от 0° до 360°.
На английский ЗПУ переводится как desired track angle (дословно – угол желаемой линии пути), или, сокращенно, desired track (DTK). Заданный путевой угол должен быть определен во время предварительной подготовки к полету и нанесен на полетную карту. На полетной карте наносятся заданные магнитные путевые углы (рис. 10.2).

Рис. 10.1. Заданный путевой угол

Рис. 10.2. Нанесение ЗМПУ на полетной карте
Заданные путевые углы не зависят от местоположения и движения ВС, они во время полета остаются постоянными, если только почему-либо не изменился сам маршрут полета. Фактические же путевые углы экипаж может изменять, меняя курс.
2. Условия полёта по линии заданного пути
Задача пилота и штурмана состоит в том, чтобы МС перемещалось по ЛЗП, то есть что бы фактическая линия пути совпадала с заданной. Для этого необходимо выполнение двух условий: ЛБУ=0, ФПУ=ЗПУ.
Выполнения только одного из этих двух условий недостаточно. Если в какой-либо момент времени самолет находится на ЛЗП (ЛБУ=0), но вектор путевой скорости не направлен по ЛЗП (ФПУ ≠ ЗПУ), то уже в следующую секунду самолет от нее уклонится. Если же ФПУ=ЗПУ, но ВС не находится на ЛЗП, то оно будет лететь параллельно ей (рис. 10.3).

Рис. 10.3. Условие полета по ЛЗП
ЛЕКЦИЯ № 11
Тема лекции: «Авиационные карты»
План лекции
1. Аэронавигационные карты
2. Радионавигационные карты
3. Маршрутные карты
Литература
1. Ю.Н.Сарайский, И.И.Алешков Аэронавигация. Часть1. Основы навигации и Применение геотехнических средств. Учебное пособие – Санкт-Петербург, 2010
2. В.П. Бабак та ін. Безпека авіації – К.: «Техніка» - 2004
Содержание лекции
Карта – условное изображение земной поверхности, являющееся отображением поверхности земного эллипсоида на плоскость, построенное по определенному математическому закону, называемому проекцией карты. В отличие от плана, который изображает небольшой участок местности (например, план здания или садового участка) и при построении которого поверхность Земли можно считать плоской, карта охватывает значительно большую территорию, на которой кривизной Земли пренебречь нельзя. Поверхность сферы, а тем более и эллипсоида, невозможно изобразить на плоскости без искажений. Изображение неизбежно будет где-то растянуто или сжато, либо будет иметь бесконечное количество разрывов. Различают искажения расстояний между объектами, углов (пеленгов, путевых углов) и площадей. Избежать всех видов искажений одновременно, на одной и той же карте, невозможно, но можно выбрать такую проекцию, чтобы что-то одно передавалось без искажений – либо углы, либо расстояния (по какому-либо направлению), либо площади. В авиации распространены карты равноугольные, на которых углы на карте равны углам на местности. Это удобно, так как позволяет смело измерять пеленги и путевые углы на карте. Правда, при этом несколько искажаются расстояния, но проекции выбирают так, чтобы эти искажения были не очень велики. Используют также карты, выполненные в произвольных проекциях, в которых есть искажения всех элементов карты, но проекция подбирается так, чтобы эти искажения были очень малы в пределах одного листа карты. Одной из основных характеристик карты является масштаб (scale).
Различают главный и частные масштабы. Прежде, чем отображать поверхность Земли на карте, необходимо ее уменьшить. Можно считать, что Земля сначала уменьшается до размеров глобуса, а затем уже «разворачивается» на плоскость. Главный масштаб это отношение длины отрезка на глобусе к длине соответствующего ему отрезка на местности. Иными словами, это степень общего уменьшения Земли до размеров глобуса. Масштаб – это отношение (дробь) и численно записывается, например, в виде 1:500000. Это означает, что единичному отрезку на глобусе (одному миллиметру, сантиметру, метру…) соответствует 500 тысяч таких же отрезков (соответственно, миллиметров, сантиметров…) на местности. Если необходимо для удобства выяснить, например, сколько в 1 сантиметре километров, нужно просто перевести количество сантиметров (500000) в километры. Очевидно, для этого нужно мысленно зачеркнуть в знаменателе дроби пять нулей (так как в 1 километре 100 000 сантиметров). Получится, что в 1 см 5 км (так называемый натуральный масштаб). Поскольку масштаб – это дробь, он считается тем крупнее, чем меньше знаменатель.
Главный масштаб одинаков для любой точки глобуса. Но при отображении поверхности глобуса на плоскость (карту) неизбежно возникают искажения – растяжения, сжатия и т.п. В каждой точке карты их характер будет различным. И даже в одной и той же точке искажения, например, длин будут разными по различным направлениям – на север, восток и т.д. Соотношение отрезков на карте и на глобусе характеризуется частным масштабом. Он различен в каждой точке карты и по каждому направлению.
На карте всегда обозначен главный масштаб и нужно помнить, что на самом деле в разных местах карты масштабы отличаются от него. Для выполнения полетов по правилам полетов по приборам (ППП) обычно используются карты масштаба 1:2000000 (в 1 см 20 км). Для полетов по правилам визуальных полетов используются карты масштаба 1:1000000 (в 1см 10 км) и 1:500000 (в 1см 5 км). В некоторых случаях, например при съемочных полетах, когда требуется более высокая точность навигации, используются карты и более крупных масштабов (1:200000 и крупнее). В качестве обзорной (вспомогательной или, как говорят, бортовой) карты могут использоваться карты и более мелких масштабов (например, 1:4000000).
На английском языке карты, используемые для навигации, обозначают общим термином aeronautical charts, в отличие от обычных географических карт, для которых используется термин map.
В авиации используются различные карты в зависимости от масштаба, проекции и нагрузки (то есть того, какая информация на ней нанесена).
1) Аэронавигационные карты. Эти карты похожи на обычные географические, но являются более подробными. Издаются обычно в масштабах 1:1000000 и 1:2000000. Проекция их по характеру искажений произвольная (называется видоизмененной поликонической, или, что то же самое, международной проекцией), но искажения в пределах листа карты малы и при измерениях на карте ими можно в большинстве случаев пренебречь. Из географической нагрузки на карту нанесены в основном те объекты, которые могут быть использованы для ориентировки: водные и лесные массивы, населенные пункты, шоссейные (красным цветом) и железные (черным) дороги и т.д. Из специальной аэронавигационной нагрузки нанесены красными пунктирными линиями изогоны, соединяющие точки с одинаковым магнитным склонением.

Рис. 11.1. Фрагмент аэронавигационной карты
2) Радионавигационные (или маршрутные) карты выполнены в равноугольной проекции в масштабе 1:2000000. Предназначены эти карты для полетов по приборам и поэтому географической нагрузки на них немного: моря, крупные и средние реки и населенные пункты, основные озера и дороги. Мелких ориентиров на них нет. Но зато нанесено много аэронавигационной информации: координаты пунктов маршрута, расстояния и путевые углы, данные наземных радиотехнических средств навигации (координаты, частоты, позывные, время работы) и многое другое. Радионавигационные карты являются уже не столько картами, сколько документами аэронавигационной информации.
3) Маршрутные карты, выпускаемые зарубежными фирмами, имеют такое же предназначение, но выпускаются в разных масштабах, несут больше аэронавигационной нагрузки и, конечно, используют другие условные знаки. Наибольшее распространение получили карты, выпускаемые корпорацией Джеппесен (Jeppesen), которая является мировым лидером по обеспечению аэронавигационной информацией.

Рис. 11.2. Фрагмент радионавигационной карты

Рис. 11.3. Фрагмент маршрутной карты фирмы Джеппесен
ЛЕКЦИЯ № 12 (2.1)
Тема лекции: «Физические принципы измерения курса и виды курсовых приборов»
План лекции
1. Физические принципы измерения курса
2. Виды курсових приборов
Литература
1. Ю.Н.Сарайский, И.И.Алешков Аэронавигация. Часть1. Основы навигации и Применение геотехнических средств. Учебное пособие – Санкт-Петербург, 2010
2. В.П. Бабак та ін. Безпека авіації – К.: «Техніка» - 2004
Содержание лекции
Курс характеризует направление продольной оси ВС в горизонтальной плоскости, то есть показывает, куда направлен «нос» самолета. Он имеет большое значение для навигации, поскольку одновременно является и пилотажным, и навигационным элементом. Очевидно, что на борту ВС должны иметься навигационные средства для непрерывного измерения курса. Приборы для измерения курса называют курсовыми приборами или просто компасами.
Курс представляет собой угол в горизонтальной плоскости между направлением, принятым за начало отсчета и направлением проекции на эту плоскость продольной оси ВС. Для того, чтобы физически измерить этот угол с помощью технического устройства (компаса), необходимо знать оба эти направления. Очевидно, что направление продольной оси ВС всегда известно – ведь компас находится на борту. Следовательно, главная проблема заключается в том, чтобы в любой момент знать, как проходит направление начала отсчета, независимо от того, какое положение занимает самолет.
В зависимости от того, каким образом определяется направление начала отсчета, различают следующие физические принципы измерения курса и, соответственно, виды компасов.
1) Магнитный принцип. Основанные на нем курсовые приборы называют магнитными компасами. Направлением начала отсчета служит направление горизонтальной составляющей вектора напряженности магнитного поля Земли, называемое северным направлением магнитного меридиана. Это направление непрерывно определяется чувствительным элементом магнитного компаса. Магнитный компас является самым древним навигационным приборам. В литературе часто упоминается, что он был изобретен в Китае еще до нашей эры, но это утверждение у многих ученых вызывает сомнения. Точно известно, что в Европе магнитные компаса для морской навигации начали использоваться с XII века нашей эры и непрерывно совершенствовались.
2) Гироскопический принцип. Гироскоп – это быстро вращающееся тело. В соответствии с законами механики гироскоп стремится сохранять направление оси своего вращения в пространстве. В гироскопических компасах гироскоп помещают в специальное устройство – карданов подвес, который обеспечивает ему три степени свободы и дает возможность гироскопу сохранять свое направление, независимо от эволюций самолета (кренов, тангажа,. разворотов). Направление горизонтально расположенной оси гироскопа и служит направлением начала отсчета при использовании гироскопических компасов.
3) Астрономический принцип. В вычислителе астрономического компаса непрерывно рассчитывается истинный курс. Для этого рассчитывается пеленг небесного светила (Солнца, Луны, звезды) в данный момент времени относительно меридиана места самолета и измеряется угол между продольной осью ВС и направлением на светило.
4) Инерциальный принцип. Инерциальные навигационные системы основаны на измерении ускорений ВС по трем осям системы координат и позволяют определять в полете большое количество различных навигационных параметров. С точки зрения измерения курса ВС инерциальные системы традиционного типа используют гироскопический принцип. В таких системах устройства для измерения ускорений – акселерометры - установлены на стабилизируемой с помощью точных гироскопов платформе, которая на протяжении всего полета сохраняет горизонтальное положение и сориентирована по меридиану. В этом случае не составляет проблемы измерить и отобразить на индикаторах угол между осью гироплатформы и продольной осью самолета, то есть курс. Но в инерциальных системах нового поколения, бесплатформенных системах, курс определяется другим способом, что позволяет отнести его к отдельному принципу определения курса. В таких бесплатформенных системах непрерывно измеряется угловая скорость поворота ВС вокруг трех перпендикулярных осей, что позволяет в любой момент определить угол, на который повернута каждая ось (в том числе – продольная ось ВС) относительно первоначального положения. Поэтому, если в начальный момент времени курс был известен, то его можно расчетным путем определить и в любой последующий момент времени. Независимо от принципа действия любой компас включает в себя чувствительный элемент и индикатор (указатель). Чувствительный элемент – это та часть компаса, которая непосредственно определяет направление начала отсчета курса. Индикатор предназначен для отображения измеренного курса экипажу и, как правило, представляет собой круговую шкалу, на которой напротив стрелки или специального индекса можно отсчитать курс. Если чувствительный элемент и индикатор конструктивно совмещены, то такие компаса называют совмещенными. Разумеется, они размещаются в кабине экипажа, поскольку индикатор должен располагаться на приборной доске.
Если же индикатор находится в кабине экипажа, а чувствительный элемент в другом месте ВС, то компаса называют дистанционными. В настоящее время практически все курсовые приборы являются дистанционными.
ЛЕКЦИЯ № 13 (2.2)
Тема лекции: «Основные сведения про магнитное поле Земли. Понятие девиации магнитного компаса»
План лекции
1. Элементы земного магнетизма
2. Понятие о девиации
3. Девиация магнитного компаса
Литература
1. Ю.Н.Сарайский, И.И.Алешков Аэронавигация. Часть1. Основы навигации и Применение геотехнических средств. Учебное пособие – Санкт-Петербург, 2010
2. В.П. Бабак та ін. Безпека авіації – К.: «Техніка» - 2004
Содержание лекции
Принцип действия магнитных компасов основан на использовании магнитного поля Земли. Как и у большинства других планет у Земли имеется магнитное поле. Предполагается, что оно вызвано конвективным перемещением в ядре планеты расплавленных металлических масс. Если эти массы имеют электрический заряд, то их движение представляет собой электрический ток, который, в соответствии с законами физики, и вызывает магнитное поле. Магнитные силовые линии выходят и входят в поверхность Земли в точках, называемых геомагнитными полюсами (рис. 13.1). Эти полюса не совпадают с географическими полюсами и, кроме того, медленно перемещаются.

Рис. 13.1. Силовые линии магнитного поля Земли
Структура магнитного поля Земли является сложной. В первом приближении можно считать, что внутри планеты находится огромный магнит (диполь), ось которого наклонена к оси вращения Земли под углом примерно 11,5°. Этот условный диполь и создает примерно 70% магнитного поля. Однако региональные и местные магнитные аномалии вызывают искривление силовых линий в разных местах планеты. В любой точке пространства магнитное поле можно характеризовать вектором его напряженности Т. Этот вектор направлен по касательной к магнитной силовой линии в данной точке. Модуль его в системе СИ измеряется в амперах на метр (А/м), но часто в литературе приводятся значения и в единицах по старым системам: в эрстедах (Э) и гаммах (γ).
Соотношение между этими единицами следующее: 1 Э = 79,6 А/м, 1 γ = 10-5 Э.
Гамма является просто более мелкой единицей измерения по сравнению с эрстедом и, следовательно, более удобной для описания магнитного поля Земли, поскольку напряженность его невелика. Действительно, в разных точках планеты она не превышает 0,6…0,7 Э, а на территории России в среднем составляет 0,2…0,4 Э. Для сравнения можно заметить, что самые сильные современные электромагниты создают напряженность 100 000 Э и более. Часто интенсивность магнитного поля характеризуют также величиной магнитной индукции. Магнитная индукция B характеризует импульс напряжения, индуцируемый в пробном соленоиде (катушке) при помещении его в магнитное поле. Единицей измерения индукции является Тесла (Тл). Напряженность поля в 1 гамму соответствует создаваемой ею в вакууме индукции величиной в 1 нанотеслу, то есть 10-9 Тл. Поскольку вектор напряженности Т направлен по касательной к силовым линиям, он в общем случае не лежит в плоскости горизонта и, вследствие искривления силовых линий, не совпадает с плоскостью географического меридиана. Если разместить в какой-либо точке начало прямоугольной системы координат и направить ось ОХ по меридиану на север, ось ОУ перпендикулярно к ней на восток, а ось OZ направить вниз, то вектор Т можно разложить на горизонтальную составляющую Н и вертикальную Z (рис. 13.2). Направление горизонтальной составляющей Н является очень важным для аэронавигации, так как это направление и называют северным направлением магнитного меридиана в данной точке. Очевидно, что угол между осью ОХ (направлением истинного меридиана) и вектором Н (направлением магнитного меридиана), есть не что иное, как магнитное склонение ΔМ в данной точке. Угол θ между горизонтальной плоскостью и направлением вектора напряженности Т называется магнитным наклонением.

Рис. 13.2. Элементы земного магнетизма
Очевидно, что в магнитных полюсах, где силовые линии входят в Землю или выходят из нее, магнитное наклонение равно +90° и -90°. В районах магнитных полюсов вертикальная составляющая поля Z максимальна, а горизонтальная составляющая H очень мала. Это имеет важное значение для аэронавигации. Ведь чувствительный элемент любого магнитного компаса реагирует именно на горизонтальную составляющую. Поэтому в полярных районах магнитные компаса работают неустойчиво. В экваториальных районах, где силовые линии идут примерно параллельно к поверхности Земли, магнитное наклонение близко к нулю, а горизонтальная составляющая H наибольшая.
Подвешенная на острие иглы намагниченная стрелка обычного туристского компаса, которая и является его чувствительным элементом, под действием магнитного поля стремится занять положение, соответствующее направлению вектора T. А если заставить эту стрелку располагаться горизонтально, то она будет направлена по направлению вектора H.
Из-за неоднородности магнитного поля в разных местах планеты направление вектора H (северное направление магнитного меридиана) составляет разный угол (магнитное склонение) с направлением истинного (географического) меридиана. В земной коре в разных местах имеется большое количество намагниченных пород, которые вызывают искривления магнитных силовых линий. В таких районах, называемых районами магнитных аномалий, магнитное склонение резко отличается по величине и знаку от значений, прилегающих к данному району. В Российской Федерации это районы Курской, Магнитогорской и других аномалий. Из-за искривления силовых линий северный конец стрелки туристского компаса вовсе не показывает направление ни на географический, ни на магнитный полюсы. Это просто направление вектора напряженности именно в данной точке.
Как уже отмечалось, на аэронавигационных картах наносят линии (изогоны), соединяющие точки с одинаковым магнитным склонением. Из-за неоднородности магнитного поля и магнитных аномалий изогоны могут быть довольно извилистыми. Местные аномалии оказывают влияние лишь до высот 3-4 тысячи метров, поэтому на больших высотах изогоны становятся более правильными, искривления менее выражены. На рис. 13.3 показана карта изогон для большей части территории планеты без учета местных аномалий. Магнитное поле медленно меняется, соответственно изменяется и фактическое расположение изогон. Это необходимо учитывать при определении магнитного склонения по аэронавигационным картам. На них всегда указано, на какой год э(поху) нанесены изогоны. Эпохи устанавливаются кратными пяти годам (2000, 2005, 2010 г.г. и т.д.). Магнитное поле Земли также подвержено нерегулярным и подчас сильным изменениям, вызванным главным образом воздействием Солнца. Во время так называемых магнитных бурь магнитное склонение может непредсказуемо меняться на единицы и даже десятки градусов, что делает невозможным применение магнитных компасов.
Магнитный компас предназначен для измерения магнитного курса, то есть угла между северным направлением магнитного меридиана и продольной осью самолета. Как уже отмечалось, северным направлением магнитного меридиана называют направление горизонтальной составляющей магнитного поля Земли H в данной точке. Именно на эту составляющую и реагирует чувствительный элемент магнитного компаса.
Но компас расположен на ВС, которое имеет собственное поле. Оно вызвано намагниченными металлическими массами, входящими в состав конструкции ВС, а также электрическими токами, протекающими в многочисленных электрических цепях ВС. Обозначим вектор напряженности собственного поля самолета F. Очевидно, что в одной и той же точке пространства не могут одновременно существовать два магнитных поля, два вектора напряженности – Земли (H) и самолета (F). Эти два вектора векторно складываются, образуя некоторое суммарное, результирующее поле
с вектором напряженности, который обозначим R (рис.13.4).
Естественно, что чувствительный элемент магнитного компаса и реагирует на это результирующее поле, поскольку только оно и существует в данной точке. И если разместить на самолете туристский компас, то его намагниченная стрелка встанет по направлению вектора R, то есть отклонится от настоящего направления магнитного меридиана. Это явление называется девиацией магнитного компаса. Девиация – означает отклонение.
Поскольку направление R не совпадает с направлением магнитного меридиана (вектора H), то и измеренный компасом курс не будет правильным – ведь он будет измерен от направления вектора R. В навигации для удобства любые направления начала отсчета углов называют северным направлением какого-то меридиана – истинного, магнитного… Поэтому и направление вектора R называют северным направлением компасного меридиана, а измеренный от него курс – компасным курсом.

Рис. 13.3. Изогоны на карте мира

Рис. 13.4. Результирующий вектор магнитного поля
Угол между векторами H и R также называют девиацией. Девиация(deviation) ΔК – угол, заключенный между северными
направлениями магнитного и компасного меридианов (рис. 13.5). Отсчитывается от северного направления магнитного меридиана к востоку с плюсом, а к западу с минусом. Соответственно, девиация теоретически может лежать в диапазоне ±180°, хотя фактически имеет, конечно, гораздо меньшие значения.
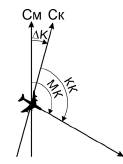
Рис. 13.5. Девиация
Таким образом, компасный курс (γк, КК), то есть то значение, которое показывает магнитный компас, не совпадает с магнитным курсом (γм, МК). то есть фактическим направлением продольной оси ВС относительно магнитного меридиана. Они отличаются на величину девиации: ΔК =МК-КК.
Очевидно, что если величина девиации ΔК известна, то, сняв показания магнитного компаса (КК), можно найти и магнитный курс: МК=КК+ ΔК.
И наоборот, можно определить, какой КК необходимо выдерживать, чтобы МК был равен требуемому значению: КК=МК- ΔК.
Для того, чтобы не ошибиться со знаками при переходе от одного вида курса к другому, следует руководствоваться уже упоминавшимся правилом учета поправок в навигации: при переходе от приборных величин к истинным поправки прибавляются, а при переходе от истинных к приборным – вычитаются. Очевидно, что в данном случае самым приборным является компасный курс – ведь это и есть значение, непосредственно снимаемое с прибора. Магнитный курс по сравнению с ним является более правильным, более «истинным». Ну, а истинный курс, разумеется, более «истинный», чем магнитный, поскольку отсчитывается от географического (истинного) меридиана.
За рубежом для правильного учета девиации используется правило: «Deviation west – compass best. Deviation east – compass least».

Рис. 13.6. Правило учета поправок
Важно помнить, что величина девиации зависит от курса самолета. Для каждого компаса в кабине экипажа имеется график или таблица, по которой пилот может определить величину девиации в зависимости от показаний компаса (компасного курса).
ЛЕКЦИЯ № 14 (2.3)
Тема лекции: «Гироскопический принцип измерения курса. Курсовой гироскоп на самолёте»
План лекции
1. Измерение курса
2. Гироскопический принцип измерения курса
3. Курсовой гироскоп на самолёте
Литература
1. Ю.Н.Сарайский, И.И.Алешков Аэронавигация. Часть1. Основы навигации и Применение геотехнических средств. Учебное пособие – Санкт-Петербург, 2010
2. В.П. Бабак та ін. Безпека авіації – К.: «Техніка» - 2004
Содержание лекции
Гироскоп (от древнегреческих слов, означающих «вращение» и «смотреть») – это в принципе любое вращающееся тело. В современной технике гироскоп представляет собой достаточно массивный ротор с большой скоростью вращения (несколько тысяч оборотов в минуту).
Основным физическим свойством любого гироскопа является то, что он стремится сохранять направление оси своего вращения в пространстве. Это является следствием общего свойства инертности материи – ведь каждая точка вращающегося тела стремится сохранять скорость и направление своего движения. В наличии у гироскопа такого свойства убедился каждый, кто имел дело с обычным игрушечным волчком или, например, раскрутив велосипедное колесо, пытался повернуть его ось.
Идея устройства гироскопических компасов проста. Если на борту, несмотря на развороты ВС, все время сохраняется некоторое постоянное направление (направление оси вращения гироскопа), то его можно принять за направление начала отсчета и отсчитывать от него угол до направления продольной оси ВС, то есть курс, и другие пилотажные элементы. Разумеется, если ось гироскопа жестко закрепить на самолете, то она просто вынуждена будет поворачиваться вместе с ним и тогда никакое направление начала отсчета не сохранится. Поэтому гироскоп помещают в специальное устройство – карданов подвес, который обеспечивает гироскопу три степени свободы, то есть дает ему возможность свободно вращаться вокруг трех перпендикулярных осей. Карданов подвес (назван в честь Д. Кардана, который впервые описал его в своей книге) представляет собой две рамки, одна внутри другой, соединенные между собой в противоположных точках. Если внутри рамок поместить какое-нибудь тело, то оно будет сохранять свое положение, как бы рамки ни вращались вокруг него. Считается, что это устройство было изобретено в Китае во II веке до нашей эры. Поскольку курс измеряется в горизонтальной плоскости, ось курсового гироскопа, то есть гироскопа, предназначенного для измерения курса, должна располагаться горизонтально. Если эту ось направить по какому-либо выбранному направлению, например, по северному направлению меридиана данной точки, то она будет сохранять это направление, как бы ни вращалось ВС вместе с кардановым подвесом «вокруг» гироскопа. Остается только каким-либо образом измерить и передать на указатель компаса угол между осью гироскопа и продольной осью самолета и тогда можно отсчитывать курс относительно выбранного направления начала отсчета (в данном случае – от северного направления меридиана).
Гирополукомпас ГПК-52. Принцип работы гироскопических курсовых приборов рассмотрим на примере одного из простейших устройств такого рода, еще применяющихся на ВС, - гирополукомпаса ГПК-52. Основной частью прибора является гироузел массой около 2 кг, представляющий собой ротор гироскопа вместе с электродвигателем, приводящим его во вращение со скоростью 22-23 тыс. оборотов в минуту.
Гироскоп помещен в карданов подвес из двух рамок. Во внутренней рамке на подшипниках закреплена ось гироскопа в горизонтальном положении. Сама внутренняя рамка также может вращаться вокруг горизонтальной оси, перпендикулярной оси гироскопа. Ось внутренней рамки также в свою очередь закреплена в подшипниках во внешней рамке, которая может
вращаться вокруг вертикальной оси. Эта внешняя ось жестко закреплена в корпусе ГПК-52, который размещен в кабине самолета и, естественно, поворачивается вместе с самолетом.
На оси внешней рамы карданова подвеса закреплена шкала отсчета курсов. ГПК-52 часто монтируется на штурманском столике в кабине






