Принципы и методы, положенные в основу обработки результатов измерений и их оценки, применимы главным образом к случайным погрешностям.
Для оценки возможной погрешности измерений необходимо знать закономерности появления случайных погрешностей. При большом числе измерений их значения, как правило, распределяются по закону Гаусса: погрешности измерений могут принимать непрерывный ряд значений; вероятность (частота) появления погрешностей, равных по значению и обратных по знаку, одинакова; большие по абсолютному значению погрешности встречаются реже малых; средняя арифметическая погрешность стремится к нулю при увеличении числа измерений.
При измерениях необходимо учитывать, что:
среднее арифметическое из случайных погрешностей измерений одной и той же физической величины, произведенных при одинаковых условиях, приближается к нулю при возрастании числа измерений;
чем больше абсолютная величина погрешности, тем реже она встречается в ряду измерений, одинаковых по точности;
по абсолютной величине случайные погрешности практически не могут превосходить определенного предела, величина которого зависит от условий измерений и их точности.
Перечисленные особенности случайных погрешностей с очевидностью проявляются только статистически, т. е. при довольно большом числе измерений, но их учитывают и при малом числе измерений, хотя в этом случае они не столь очевидны.
В качестве наилучшего (более надежного) значения истинной физической величины принимают среднее арифметическое 
из результатов измерений 
, (3)
где п — количество измерений одной и той же величины.
Мерой точности измерении служит среднее квадратическое отклонение S
, (4)
где Δ i — абсолютные погрешности.
Если неизвестно номинальное или действительное значение измеряемой величины, среднее квадратическое отклонение определяют по формуле
, (5)
где d i — разность между измеренные значением физической величины xi и средним арифметическим 
.
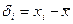. (6)
Всегда имеет место равенство 
, которое используется для контроля вычислений среднего арифметического.
При увеличении числа измерений среднее квадратическое отклонение стремится к своему статистическому пределу s, называемому стандартом распределения погрешностей.
Оценка грубых погрешностей.
Одной из разновидностей случайных погрешностей являются грубые ошибки, значительно превосходящие как случайные, так и систематические погрешности. Они приводят к явному браку, и их отсутствие в измерениях и вычислениях должно быть полностью гарантировано путем обязательного повторения измерений.
Грубыми называют погрешности, явно превышающие по своему значению погрешности, оправданные условиями проведения эксперимента. Если исполнитель в процессе измерений обнаруживает, что результат одного из наблюдений резко отличается от других, и находит причины этого, тоонможетотбросить этот результат и провести повторные измерения.
Особенно остро ставится вопрос об устранении грубых погрешностей при обработке уже имеющегося материала, когда невозможно учесть все обстоятельства, при которых проводили измерения. В этом случае приходится прибегать к чисто статистическим методам.
Вопрос о том, содержит ли данный результат наблюдений грубую погрешность, решается общими методами проверки статистических гипотез.
Проверяемая гипотеза состоит в утверждении, что результат наблюдения xi не содержит грубой погрешности, т. е. является одним из значений случайной величины Х с законом распределения FX(x), статистические оценки параметров которого предварительно определены. Сомнительным может быть в первую очередь лишь наибольший xmах или наименьший xmin из результатов наблюдений. Поэтому для проверки гипотезы следует воспользоваться распределениями величин
или 
.
Функции их распределения определяют методами теории вероятностей. Они совпадают между собой и для нормального распределения результатов наблюдений табулированы и представлены в табл. 1 Приложения. По данным этой таблицы, при заданной доверительной вероятности a или уровне значимости q = 1 — a можно для чисел измерения п = 3425 найти те наибольшие значения na, которые случайная величина n может еще принять по чисто случайным причинам.
Если вычисленное по опытным данным значение n окажется меньше na, то гипотеза принимается, в противном случае ее следует отвергнуть как противоречащую данным наблюдений. Тогда результат Xmах или соответственно Xmin приходится рассматривать как содержащий грубую погрешность и не принимать его во внимание при дальнейшей обработке результатов наблюдений.
Пример. При измерении температуры были получены следующие результаты: 20,42; 20,43; 20,40; 20,43; 20,42; 20,43; 20,39; 20,30; 20,40; 20,43; 20,42; 20,41; 20,39; 20,39; 20,40.
Требуется определить, не содержит ли результат восьмого наблюдения t8 = 20,30° С грубой погрешности.
Вначале обычными способами находим среднее арифметическое и среднее квадратическое отклонение результатов наблюдений:
Если принять доверительную вероятность a = 0,95, тоизтабл. 11 Приложения при п = 15, n0,95 = 2,493 и, поскольку
результат t8 = 20,30° С содержит грубую погрешность.
Если отбросить этот результат и повторить вычисления,то среднее арифметическое окажется равным 
, а среднее квадратическое отклонение уменьшится до 
. Расчет приведен в последних двух графах таблицы.
лабораторной работе 3.
Модели обработки данных измерений.
Формирование модели данных является одним из этапов процесса измерения. Модель служит наглядным примером зависимости групп результатов измерений между собой. Для построения моделей в лабораторной работе применяется регрессионный анализ. С его помощью подбираются кривые заданного вида.
Статистическая модель строится путем проверки полученной регрессионной модели статистическими методами.
Ниже приведен пример построения регрессионной модели.
Пример. С помощью метода наименьших квадратов подберем кривую вида
Y = bo+b1x+b2ez
к четырем (трехмерным) точкам:
(х 1, z 1, y 1) = (3; 1; 8,2),
(х 2, z 2, y 2) = (20; 3; 60,3),
(х 3, z 3, y 3) = (1; 0; 3,1),
(х 4, z 4, y 4) = (55; 4; 164,3).
Независимыми переменными в данной регрессии являются х и z, зависимой переменной – у. Проверим регрессионное уравнение на значимость и найдем доверительные границы для неизвестного параметра β0 и σ2.
Прямая линия содержит нулевую и первую степень х, а при построении прямой линий по методу наименьших квадратов мы используем матрицу Х с двумя столбцами, один из которых составлен из нулевых степеней { xi }, а другой—из первых степеней { xi }. При подгонке по экспоненциальной кривой, содержащей константу и член, пропорциональный ряду еx, возьмем матрицу Х также с двумя столбцами, один из которых составлен из единиц, а второй—из значений {exp xi }. Для подгонки по кривой примера матрица X должна иметь уже три столбца. Первый, второй и третий столбцы составлены соответственно из единиц, значений { xi } и значений {exp zi }. Как обычно, { yi } образуют вектор-столбец у, а коэффициенты регрессии – трехмерный вектор-столбец b. Итак,
и 
Поэтому
и
Нормальные уравнения имеют вид:
4 bo + 79 b1 + 78,40196878 b2 = 235,9,
79 bo + 3435 b1 + 3413,763836 b2 = 10270,2,
78,40196878 bo + 3413,763836 b1 + 3392,775836 b2 = 10207,02384.
Находим: bo = – 0,001022462, b1 = 0,293743778 и b2 = 2,712920796, поэтому выравненные значения равны соответственно 8,255; 60,364; 3,006 и 164,275.
В работе необходимо выполнить построение модели по группам данных индивидуального задания.
ПРИЛОЖЕНИЕ 1
| Лабораторная работа № 1. | Дата и Ф.И.О. исполнителя: | ||||||||
| Определение основных метрологических показателей и классификационных признаков (на примере средств измерения линейных величин). | |||||||||
| Цель: | 1.Научиться классифицировать с.и. | ||||||||
| 2.Определять метрологические свойства. | |||||||||
| Задачи работы: | |||||||||
| 1. Выполнить систематизацию предложенных с.и. с помощью электронных и литературных источников | |||||||||
| 2. Определить метрологические показатели с.и., используя паспортные характеристики и сами средства | |||||||||
| 3. Указать принадлежность составляющей суммарной погрешности соответствующему с.и. | |||||||||
| Систематизация средств измерений | Таблица 1 | ||||||||
| Название | Метод измерения | Характер показаний | Принцип действия | Назначение | Вид отсчета | Вид измерения | |||
| Штангенциркуль | |||||||||
| Микрометр | |||||||||
| Микроскоп | |||||||||
| Метрологические характеристики | Таблица 2 | ||||||||
| Название | Цена деления, мм | Диапазон, мм | Предел изм-я, мм | Погрешность изм-я, мм | Класс точности | Номер (по паспорту) | |||
| Штангенциркуль | |||||||||
| Микрометр | |||||||||
| Микроскоп | |||||||||
| Вывод: | В ходе работы выполнена классификация с.и. и определены их метрологические характеристики. | ||||||||
| Определены основные составные части измерительных средств: | |||||||||
| ш / циркуль: | |||||||||
| микрометр: | |||||||||
| микроскоп: | |||||||||
| Погрешности измерения | Таблица 3 | ||||||||
| Погрешность | Средство измерения | ||||||||
| ШЦ | Микрометр | Микроскоп | В таблице 3 следует распределить составляющие | ||||||
| инструментальная | суммарной погрешности по логически связанным | ||||||||
| отсчитывания | группам. | ||||||||
| от параллакса | Знаком "+" отметить составляющие погрешности, | ||||||||
| интерполяции | влияющие на точность результата при измерении | ||||||||
| от перекоса | соответствующим с.и. | ||||||||
| внешняя | Знаком "-" отметить составляющие погрешности, | ||||||||
| метода измерения | не характерные для данного с.и. | ||||||||
| систематическая | Обосновать выбор. | ||||||||
| случайная | |||||||||
| грубая | |||||||||
| Вывод: | В ходе работы определили составляющие суммарной погрешности | ||||||||
| для предлагаемых средств измерений. | |||||||||
| Контрольные вопросы: | |||||||||
| 1. | Какие классификационные группы и признаки средств измерений вы знаете? | ||||||||
| 2. | Укажите основные метрологические характеристики и дайте их определения. | ||||||||
| 3. | Перечислите составные части рассматриваемых в работе средств измерений. | ||||||||
| 4. | Какие общие группы погрешностей вы знаете? | ||||||||
| 5. | Дайте определения для перечисленных в таблице 3 составляющих суммарной погрешности. |
ПРИЛОЖЕНИЕ 2
| Значения na при различных числах измерения n | Таблица 1 | ||||||||
| n | q=1-a | n | q=1-a | ||||||
| 0,10 | 0,05 | 0,025 | 0,01 | 0,10 | 0,05 | 0,025 | 0,01 | ||
| 1,406 | 1,412 | 1,414 | 1,414 | 2,297 | 2,461 | 2,602 | 2,759 | ||
| 1,645 | 1,689 | 1,710 | 1,723 | 2,326 | 2,493 | 2,638 | 2,808 | ||
| 1,731 | 1,869 | 1,917 | 1,955 | 2,354 | 2,523 | 2,670 | 2,837 | ||
| 1,894 | 1,996 | 2,067 | 2,130 | 2,380 | 2,551 | 2,701 | 2,871 | ||
| 1,974 | 2,093 | 2,182 | 2,265 | 2,404 | 2,557 | 2,728 | 2,903 | ||
| 2,041 | 2,172 | 2,273 | 2,374 | 2,426 | 2,600 | 2,754 | 2,932 | ||
| 2,097 | 2,237 | 2,349 | 2,464 | 2,447 | 2,623 | 2,778 | 2,959 | ||
| 2,146 | 2,294 | 2,414 | 2,540 | 2,467 | 2,644 | 2,801 | 2,984 | ||
| 2,190 | 2,383 | 2,470 | 2,606 | 2,486 | 2,664 | 2,823 | 3,008 | ||
| 2,229 | 2,387 | 2,519 | 2,663 | 2,504 | 2,683 | 2,843 | 3,030 | ||
| 2,264 | 2,426 | 2,562 | 2,714 | 2,520 | 2,701 | 2,862 | 3,051 | ||
| 2,537 | 2,717 | 2,880 | 3,071 |
Основные термины метрологии
(согласно ГОСТ 16263-70)
Физическая величина (краткая форма - величина) обозначает свойство, общее в качественном отношении многим физическим объектам (физическим системам, их состояниям и происходящим в них процессам), но индивидуальное в количественном отношении для каждого объекта.
Размер физической величины (размер величины) отражает количественное содержание в данном объекте свойства, соответствующего понятию "физическая величина".
Значение физической величины (значение величины) дает оценку физической величины в виде некоторого числа (числовое значение) принятых для нее единиц. Например, 5 кг, 5 - значение массы тела.
Единица физической величины (единица величины) - величина, которой по определению присвоено числовое значение, равное 1.
Размерность физической величины (размерность величины) - выражение, отражающее связь с основными величинами системы, в котором коэффициент пропорциональности принят равным 1.
Основная физическая величина (основная величина) - физическая величина, входящая в систему и условно принятая в качестве независимой от других величин этой системы. Например, длина 
, масса 
, время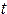 
- в механике.
Система физических величин (система величин) - совокупность физических величин, связанных между собой зависимостями.
Основная единица физической величины (основная единица) - единица основн,ой физической величины, выбранная произвольно при построении системы единиц.
Производная единица физической величины (производная единица) - единица производной физической величины, образуемой по определяющему эту единицу уравнению из других единиц данной системы единиц.
Средства измерений представляют собой технические средства, служащие для определения размеров измеряемых величин и имеющие нормированные метрологические свойства.
ЛИТЕРАТУРА
1. Борисенков Б.Г., Андреева Ф.В. Метрологическое обеспечение строительного производства. – М.: Стройиздат, 1990.
2. Бурдун Г.Д., Марков Б.Н. Основы метрологии. – М.: Изд-во стандартов, 1972.
3. Поллард Дж. Справочник по вычислительным методам статистики. – М.: Финансы и статистика, 1982.
4. Статистические методы повышения качества / Под. ред. Х.Кумэ. – М.: Финансы и статистика, 1990.
5. Тюрин Н.И. Введение в метрологию. – М.: Изд-во стандартов, 1973.
