Цель работы: Закрепить лекционный материал по изучению материала одноименной темы, реализовав матрицы переноса, масштабирования, отражения и вращения применительно к координатам описанной в программе плоской фигуры (многоугольника) с целью демонстрации движения и преобразования формы этой фигуры на плоскости.
Краткие теоретические сведения
Система координат - совокупность правил, ставящих в соответствие каждой точке набор чисел(координат), число которых называется размерностью пространства. Допустим, на плоскости введена прямолинейная координатная система, тогда каждой точке ставится в соответствие упорядоченная пара чисел (x,y) - ее координат.
В компьютерной графике чаще всего используют аффинную и декартовую систему координат. Это прямоугольная координатная система, в которой выбирается точка О - начало координат и два приложенных к ней неколлинеарных единичных вектора ex и ey, которые задают оси координат. Если единичные отрезки на осях не равны, система называется аффинной, если равны и угол между осями координат прямой - прямоугольной декартовой.
Однородным представлением n-мерного объекта является его представление в (n+1)-мерном пространстве, полученное добавлением еще одной координаты - скалярного множителя. При решении задач компьютерной графики однородные координаты обычно вводятся так: произвольной точке М(x,y) на плоскости ставится в соответствие точка M(x,y,1) в пространстве.
Если нам необходимо преобразовать точку на плоскости с координатами (x,y) в другую точку то задача сводится к поиску новых координат для этой точки - (x). В случае аффинных преобразований такой поиск сведется к решению уравнений

где a, b, c, d, m, n - произвольные числа, причем: 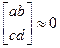 .
.
В случае, когда m и n не равны нулю, для представления преобразования в матричной форме нужно исходные и преобразованные координаты точки записать в однородных координатах (x,y,1) и ( ). Тогда в матричной форме общий вид преобразования будет следующим
). Тогда в матричной форме общий вид преобразования будет следующим
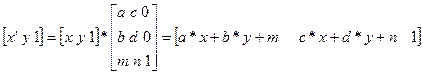
Наибольшее распространение получили частные случаи аффинных преобразований:
1. Единичное преобразование. Единичная матрица оставляет точку неподвижной. 
2. Сдвиг или плоско-параллельный перенос. Матрица переводит точку на m единиц вдоль оси x и на n -вдоль оси y:  .
.
3. Вращение вокруг начала координат. Его матрица осуществляет поворот точки объекта на угол g против часовой стрелки: 
4. Вращение вокруг произвольного центра осуществляет поворот вокруг точки (m,n) на угол g против часовой стрелки. Преобразование выполняется как последовательность трех элементарных:
· сдвиг центра вращения (m,n) в начало координат с помощью матрицы сдвига
· поворот на угол g вокруг начала координат с помощью матрицы вращения
· сдвиг точки (m,n) в исходное положение, используя матрицу сдвига
Итоговое преобразование будет выглядеть так:
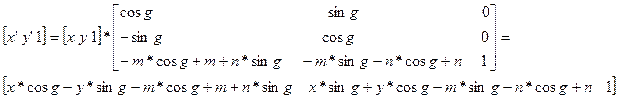
5.Симметрия относительно оси, проходящей через начало координат осуществляется преобразованием вида

При этом, если угол между осью симметрии и осью Ох = w, то угол g=2*w.
Согласно этому, симметрия относительно оси Ох
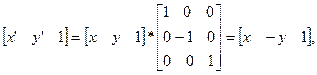
оси Оy 
оси y=x 
оси y=-x 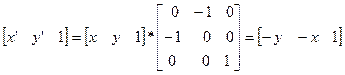 .
.
6.Масштабирование – увеличение (уменьшение размеров изображения) - в общем случае изменяет форму объекта. Назначается точка, относительно которой производится преобразование.
Масштабирование относительно точки О - начала координат

где kx,ky - коэффициенты искажения по осям Ox, Oy соответственно.
При kx=ky=k осуществляется преобразование подобия, при kx # ky изображение искажается. Изображение увеличивается при k > 1 и уменьшается при k < 1.
Масштабирование относительно произвольной точки с координатами (m, n)

Матрица любого аффинного преобразования может быть получена умножением соответствующих рассмотренных здесь простых матриц. Порядок умножения имеет значение, поэтому выполнять его надо в определенной логической последовательности.
Если координаты точек объекта представлены вектором - столбцом, а не вектором - строкой, соответствующая матрица для преобразований должна быть транспонирована.
Для возвращения к исходному состоянию следует использовать матрицу обратную той, что использовалась при преобразовании.
Для эффективной работы с преобразованиями следует руководствоваться следующими рекомендациями:
- лучше умножение на результирующую матрицу, чем последовательность умножений
- лучше масштабировать, а потом поворачивать, чем поворачивать, а затем масштабировать
- если комбинированное преобразование содержит поворот, то его следует делать отдельно и последним
- для того, чтобы движение казалось непрерывным и плавным, следует выводить кадры достаточно быстро (30-60 мсек) и координаты каждой точки преобразовывать быстрее.
В уравнении для поворота, например, если угол поворота g равен нескольким градусам, то cos g можно принять равным единице, тогда  Еще лучше
Еще лучше 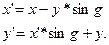
Для того, чтобы не накапливалась ошибка округлений, следует сохранять и после каждого поворота на 360 градусов использовать исходные координаты преобразуемых точек.
Задание на лабораторную работу:
Написать на языке PASCAL программу:
1. Рисующую многоугольник.
2. Смещающую его на n пикселов вправо и m вниз.
3. Зеркально отражающую его относительно осей координат.
4. Растягивающую (сжимающую) его вдоль координатных осей относительно некоторой заданной точки.
5. Вращающую его относительно центра с координатами (k,l) по часовой стрелке с увеличением размеров, против - с уменьшением.
Дополнительно
Задание выполнить с помощью программ работы с мышью.
Требования к защите лабораторной работы
Защита лабораторной работы состоит из демонстрации преподавателю результатов выполнения задания на лабораторную работу и ответов на задаваемые преподавателем вопросы по ходу демонстрации.
Требования к отчету
Отчет выполняется на отдельных листах формата А4. Содержит титульный лист с названием работы, оформленный согласно требованиям кафедры, распечатку программы - результат выполнения заданий лабораторной работы с обязательными комментариями.
Вопросы для самоподготовки:
1. Что такое аффинные преобразования и однородные координаты? Где и для чего однородные координаты используются в компьютерной графике?
2. Можно ли и каким образом, при помощи троек однородных координат и матриц третьего порядка описать любое аффинное преобразование плоскости?
3. Какие системы координат используются в компьютерной графике? Чем различаются мировая и приборная системы координат? Что такое абсолютные и относительные координаты, когда применяются те и другие?
4. Перечислите основные свойства аффинных преобразований, снискавшие им широкое распространение,
5. Чем характерна декартова система координат?
Литература
1. Фоли, Дж. Основы интерактивной машинной графики [текст]: В 2 кн. кн. 2 / Дж. Фоли, А. Дэм; под ред. Ю. М. Баяковского; пер. с англ. В. А. Галактионова и др. - М.: Мир, 1985. - 368c.: ил.
2. Роджерс, Д. Ф. Алгоритмические основы машинной графики [текст] / Д. Ф. Роджерс; пер. с англ. С. А. Вичеса и др.; Под ред. Ю. М. Баяковского, В. А. Галактионова. - М.: Мир, 1989. - 503c.
3. Шикин, Е. В. Компьютерная графика: Динамика, реалист. изображения [текст] / Е. В. Шикин, А. В. Боресков. - М.: ДИАЛОГ-МИФИ, 1996. - 287c.: ил.
4. Боресков, А. В. Компьютерная графика: первое знакомство [текст] / А. В. Боресков, Е. В. Шикин, Г. Е. Шикина; Под ред. Е. В. Шикина. - М.: Финансы и статистика, 1996. - 176c.: ил. - (Диалог с компьютером).






