C).
$$$17 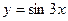 функциясының периоды: H)
функциясының периоды: H) 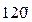 .
.
$$$ 18Функцияның тұрақтылық белгісінің тұжырымдалуы: A) Егер қандайда бір аралықта туынды нольге тең болса, онда осы аралықта функция тұрақты.
$$$ 19Функцияның монотондық белгісінің тұжырымдалуы: B) Функцияның монотондық аралықтары оның туындысының таңба тұрақтылық аралықтарымен бірдей болады.
$$$ 20Функцияның экстремумының қажетті шартының тұжырымдалуы: C) Экстремум нүктесінде туынды нольге айналады.
$$$ 21«Квадраттық функцияның ең үлкен және ең кіші мәндері» ұғымын қалыптастыру үшін оқушыларға келесі жаттығу ұсынылды: «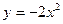 -квадраттық функция берілген. Берілген
-квадраттық функция берілген. Берілген 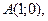
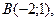

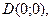
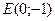 нүктелердің қайсысында квадраттық функцияның ең үлкен мәні болады?». Осы жаттығу бағытталған: E) Қалыптастырылып отырған ұғымның қасиеттерін орнатуға.
нүктелердің қайсысында квадраттық функцияның ең үлкен мәні болады?». Осы жаттығу бағытталған: E) Қалыптастырылып отырған ұғымның қасиеттерін орнатуға.
$$$ 22Жалпы білім беретін орта мектептер үшін математика бойынша бағдарламаның қайсы бөлімінде курста оқып үйренетін материалдың мүмкін болатын реті сыныптар бойынша бөлініп және тақырыпты оқуға бөлінген шамамен сағаттар саны көрсетілген: A) Оқытылатын оқу материалдарын тақырыптық жоспарлауында.
$$$ 23Жалпы білім беретін орта мектептер үшін математика бойынша бағдарламаның қайсы бөлімінде математикаға оқытудың жалпы мақсаттары мен мәселелері жазылған: B) Оқу бағдарламасына берілген түсініктеме хатта.
$$$ 24 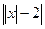 , егер
, егер 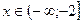 болса, өрнекті модуль таңбасынсыз жазыңыз: C)
болса, өрнекті модуль таңбасынсыз жазыңыз: C) 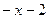
$$$ 25 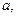
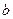 және
және 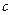 сандарының кем дегенде екеуінің теңдігін тепе-теңдік көмегімен жазыңыз: A)
сандарының кем дегенде екеуінің теңдігін тепе-теңдік көмегімен жазыңыз: A) 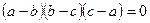 .
.
$$$ 26Сынып оқушылары бірдей тапсырмаларды орындайтын, өзіндік жұмыс формасы: A) Жаппай. F ) Жаппай, барлығында бірдей.
$$$ 27Егер 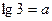 және
және 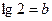 болса,
болса,  өрнегінің мәнін анықтаңыз: A)
өрнегінің мәнін анықтаңыз: A) 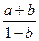 .C)
.C) 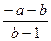 .
.
$$$ 28Теңдеулерді шешу кезінде кейбір бөгде түбірдің пайда болуына әкеліп соғатын түрлендірулер:
1) теңдеудің екі жағын белгісізі бар өрнекке бөлгенде
2) теңдеудің екі жағын жұп дәрежеге шығарғанда
3) теңдеудің екі жағынан жұп түбір алғанда
4) теңдеудің анықталу облысын кеңейтетін логарифмдік және тригонометриялық теңбе-теңдіктерді пайдаланғанда
5) теңдеудің облысын кішірейтетін логарифмдік және тригонометриялық теңбе-теңдіктерді пайдаланғанда
Көрсетілген жағдайлардың қайсысында теңдеудің бөгде түбірі пайда болады: B) 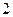 .D)
.D) 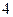 .
.
$$$ 29Берiлген функцияның қандай қасиеттерi осы функцияға қарағанда керi функцияда сақталады :A) Монотондық қасиеті. F) Өсу (кему) қасиеті.
$$$ 30Тәуелсіз айнымалының әрбір мәніне тәуелді айнымалының жалғыз ғана мәні сәйкес келетін тәуелділікті қалай атайды: A) Функция.D) Бейнелеу.
$$$ 31Оқушы жұп функцияның анықтамасын төмендегідей тұжырымдады: «Егер 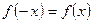 теңдігі орынды болса, онда
теңдігі орынды болса, онда 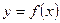 функциясы жұп деп аталады». Берілген анықтамада қандай шарт қалып қойған: B)
функциясы жұп деп аталады». Берілген анықтамада қандай шарт қалып қойған: B) 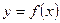 функциясының анықталу облысы координат басына қарағанда симметриялы.G) анықталу облысынан алынған кез келген
функциясының анықталу облысы координат басына қарағанда симметриялы.G) анықталу облысынан алынған кез келген  және
және 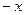 үшін.
үшін.
$$$ 32Оқушы тақ функцияның анықтамасын төмендегідей тұжырымдады: «егер 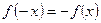 теңдігі орындалса, онда
теңдігі орындалса, онда 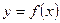 функциясы тақ деп аталады». Берілген анықтамада қандай шарт қалып қойған: B)
функциясы тақ деп аталады». Берілген анықтамада қандай шарт қалып қойған: B) 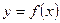 функциясының анықталу облысы координат басына қарағанда симметриялы.
функциясының анықталу облысы координат басына қарағанда симметриялы.
F) Анықталу облысынан алынған кез келген және үшін.
$$$ 33 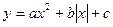 , где
, где 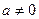 түріндегі функция графигін салудың дұрыс реті: B)
түріндегі функция графигін салудың дұрыс реті: B) 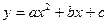 функциясының графигін салу және оның барлық
функциясының графигін салу және оның барлық  болғандағы мәндеріне сәйкес бөлігін
болғандағы мәндеріне сәйкес бөлігін  осіне қарағанда симметриялы бейнелеу.
осіне қарағанда симметриялы бейнелеу.
H) функциясының графигін салу және аргументтің барлық теріс емес болғандағы мәндеріне сәйкес бөлігін осіне қарағанда симметриялы бейнелеу.
$$$34 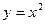 функциясы графигінің үлгісін(шаблонын) қолдана отырып,
функциясы графигінің үлгісін(шаблонын) қолдана отырып, 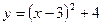 функциясының графигін салудың дұрыс ретін көрсетіңіз: A)
функциясының графигін салудың дұрыс ретін көрсетіңіз: A) 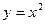 функциясының графигін
функциясының графигін 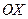 осі бойынша
осі бойынша 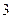 бірлікке оңға жылжыту.C)
бірлікке оңға жылжыту.C) 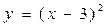 функциясының графигін
функциясының графигін 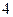 бірлікке
бірлікке  осі бойынша жоғары жылжыту.
осі бойынша жоғары жылжыту.
$$$35 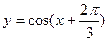 функциясының негiзгi периоды: B)
функциясының негiзгi периоды: B) 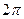 .D)
.D)  .
.
$$$ 36 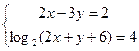
 теңдеулер жүйесінің шешімі: B)
теңдеулер жүйесінің шешімі: B) 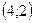 .E)
.E) 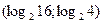 .
.
$$$ 37 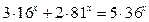 теңдеуінің шешімі: A) 0.C)
теңдеуінің шешімі: A) 0.C) 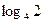 .
.
$$$ 38  функциясы қалай аталады, егер анықталу обласындағы кез келген
функциясы қалай аталады, егер анықталу обласындағы кез келген 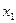 және
және 
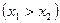 үшін
үшін  теңсіздігі орынды болса: A) Кемімейтін.G) Тең немесе өспелі.
теңсіздігі орынды болса: A) Кемімейтін.G) Тең немесе өспелі.
$$$ 39  функциясының
функциясының  нүктесі қалай аталады, егер берілген нүктенің маңайындағы барлық
нүктесі қалай аталады, егер берілген нүктенің маңайындағы барлық  үшін
үшін  теңсіздігі орындалса: A) Минимум нүктесі.D)Берілген аралықтың ең кіші нүктесі.
теңсіздігі орындалса: A) Минимум нүктесі.D)Берілген аралықтың ең кіші нүктесі.
$$$ 40Келесі өрнекті модуль таңбасынсыз жазыңыз: 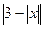 , егер
, егер 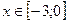 A)
A) 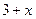 .C)
.C) 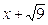 .
.
$$$ 41Теңсіздікті модуль таңбасының көмегімен жазыңыз: 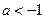 және
және 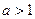 : C)
: C) 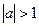 .H)
.H) 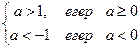 .
.
$$$ 42 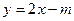 және
және 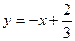 функцияларының графиктері ординатаның бір нүктесі арқылы өтетіні белгілі болғандағы,
функцияларының графиктері ординатаның бір нүктесі арқылы өтетіні белгілі болғандағы, 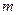 – параметрін табыңыз: B)
– параметрін табыңыз: B) 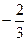 .F)
.F) 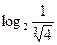 .
.
$$$ 43 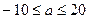 теңсіздігін модуль таңбасы көмегімен жазу: D)
теңсіздігін модуль таңбасы көмегімен жазу: D) 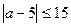 .F)
.F) 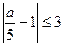 .
.
$$$ 44Теңсіздікті шешіңіз: 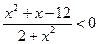 : B)
: B) 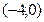 .G)
.G) 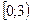 .
.
$$$45  функциясы үшін қатнасы жоқ тұжырым: A)
функциясы үшін қатнасы жоқ тұжырым: A)  функциясының графигі
функциясының графигі  осіне қарағанда симметриялы.C)
осіне қарағанда симметриялы.C)  - жұп функция.
- жұп функция.
$$$46 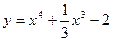 функциясының кему аралығы: B)
функциясының кему аралығы: B) 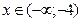 .H)
.H) 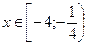 .
.
$$$47 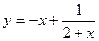 функцияның анықталу обласы: B)
функцияның анықталу обласы: B) 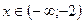 .D)
.D) 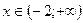 .
.
$$$ 48«Дедукция» сөзі латынша нені білдіреді: C) Қорытындылау.E) Тұжырымдау.
$$$ 49Сабақтың негiзгi дидактикалық мақсаты: ұғым енгiзу, немесе қасиеттi орнату (белгiлер, қатынастар) немесе ереже (алгоритм) құру және т.б. Осы сабақ типiн анықтаңызA) Жаңа материалмен таныстыру сабағы.H) Жаңа тақырыпты түсіндіру сабағы.
$$$ 50Теңсіздік қандай математикалық зерттеу әдістермен дәлелденеді 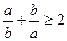 , мұндағы
, мұндағы 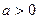 ,
,  B) Анализ.F) Синтез.
B) Анализ.F) Синтез.
$$$ 51Сабақта болатындарды толық елестетуді анықтау талап ететін, сабақты дайындау кезеңі: A) Сабақ барысы. D) Барлық сабақтың өту барысы.G) Сабақтың фотосы.
$$$ 52Негізгі білімдерді, іскерліктерді және жұмыс тәсілдерін меңгеруге бағытталған әрекеттерді еске түсірумен шектелетін оқушылардың өзіндік жұмысының түрі:A ) Үлгі бойынша.D) Алгоритм бойынша.G) Ұсынылған үлгі бойынша.
$$$ 53Өзіндік әрекетінен білім мен іскерлікті қалыпты емес, әдеттегіден тыс жағдайда қолдануды талап ететін, оқушылардың өзіндік жұмысының түрі: A) Эвристикалық.C) Бөліктеп-ізденушілік.F) Болжау мен жаңалықты іздеу.
$$$ 54Өздігінен жинаған білімдерін, іскерліктерін қолдануды және өзінің гипотезасын, пікірін ұсынуды; оқып біліп отырған объектілер туралы жаңа мәліметтерді өзі үшін ашуға үйренуді талап ететін, оқушылардың өзіндік жұмысының түрі :B) Зерттеуші.D) Зерттеуші –ізденуші.G) Творчестволық.
$$$ 55Теңдеулерді шешу кезінде түбірлердің жоғалуына әкеліп соғатын түрлендірулер:
1) теңдеудің екі жағын белгісізі бар өрнекке бөлгенде
2) теңдеудің екі жағын жұп дәрежеге шығарғанда
3) теңдеудің екі жағынан жұп түбір алғанда
4) теңдеудің анықталу облысын кеңейтетін логарифмдік және тригонометриялық тепе-теңдіктерді қолданғанда
5) теңдеудің анықталу облысын кішірейтетін логарифмдік және тригонометриялық теңбе-теңдіктерді пайдаланғанда
Көрсетілген жағдайлардың қайсысында теңдеудің түбірі жоғалады: C) 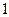 .E)
.E) 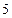 .G)
.G)  .
.
$$$ 56Пайымдардың негізі формалары: A) Жалпы және дербес, жекелік; мақұлданған және терістелген.C) Бөлімдейтін, қатаң шартты пайым F) Нақты, қажетті, мүмкін болатын пайым.
$$$ 57Аксиомалар жүйесіне қойылатын негізгі талаптар:B) Аксиомалар жүйесі қайшылықсыз болуы керек.D) Аксиомалар жүйесі толық болуы керек.G) Аксиомалар жүйесі тәуелсіз болуы керек.
$$$ 58Мәндерінің жиыны бірдей болатын f және g функциялары: A) 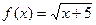 ,
, 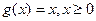 .B)
.B) 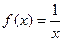 ,
, 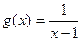 .D)
.D) 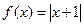 ,
, 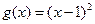 .
.
$$$ 59 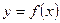 функциясының графигінің
функциясының графигінің 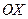 осінен төмен жатқан бөлігі, осы оське қарағанда симметриялы бейнеленетін, функцияның түрі: D)
осінен төмен жатқан бөлігі, осы оське қарағанда симметриялы бейнеленетін, функцияның түрі: D) 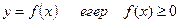 .F)
.F) 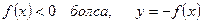
$$$ 60 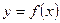 функциясының графигінің бөлігі
функциясының графигінің бөлігі  болғанда
болғанда  осіне қарағанда симметриялы бейнеленетін, функцияның түрі: A)
осіне қарағанда симметриялы бейнеленетін, функцияның түрі: A) 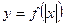 .C)
.C) 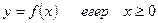 H)
H) 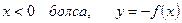 $$$ 61
$$$ 61 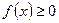 болғанда графигі сақталып, ал содан соң ол
болғанда графигі сақталып, ал содан соң ол 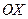 осіне қарағанда симметриялы бейнеленетін, функцияның түрі: B)
осіне қарағанда симметриялы бейнеленетін, функцияның түрі: B) 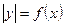 .D)
.D) 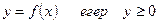 .G)
.G) 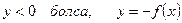 .
.
$$$ 62
Туындының көмегімен анықталатын функцияның негізгі қасиеті: A) Монотондық аралықтары және экстремум нүктелері.C) Өсуі және кемуі; экстремум нүктелері.H) Монотондылығы, максимум және минимум нүктелері.
$$$ 63Таным процесінде бөлек қолданылатын екі логикалық амал: B) Анализ және синтез.D) Жалпылау және абстракциялау.G) Салыстыру және анализ.
$$$ 64Логикалық амалға жатпайтын ойлау түрі: D) Бақылау.F) Тәжірибе. H) Өлшеу.
$$$ 65Функцияның экстремумының жеткілікті шартының тұжырымдалуы: B) Егер қандайда бір нүктеде туынды нольге айналса және сонымен бірге, туынды осы нүктеден өткенде өзінің таңбасын өзгертсе, онда осы нүктеде функция экстремумға жетеді.D) Егер  нүктеде
нүктеде 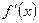 нольге айналса және сонымен бірге, туынды осы нүктеден өткенде өзінің таңбасын «-» тан «+» ке өзгертсе, онда осы нүктеде функция экстремумға жетеді.
нольге айналса және сонымен бірге, туынды осы нүктеден өткенде өзінің таңбасын «-» тан «+» ке өзгертсе, онда осы нүктеде функция экстремумға жетеді.
F) Егер белгілі бір нүктеде 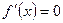 болса және сонымен бірге, туынды сол нүктеден өткенде өзінің таңбасын «+» тан «-» ке өзгертсе, онда осы нүктеде функция экстремумға жетеді.
болса және сонымен бірге, туынды сол нүктеден өткенде өзінің таңбасын «+» тан «-» ке өзгертсе, онда осы нүктеде функция экстремумға жетеді.
септеңiз::A).D).
$$$ 67Есептеңiз: 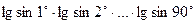 : A)
: A) 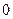 .C)
.C) 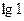 .
.
$$$ 68Есептеңiз: 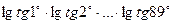 : A)
: A) 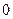 .C)
.C) 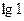 .
.
$$$ 69  - функциясының кему аралығы :B)
- функциясының кему аралығы :B) 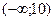 E)
E) 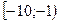 .
.
$$$ 70«Функция» сөзінің синонимі: B) Бейнелеу.E) Сәйкестік.H) Функционалдық тәуелділік.
$$$ 71Анықталу обласынан алынған кез келген  үшін
үшін 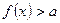 теңсіздігі орынды болатындай
теңсіздігі орынды болатындай  саны бар болатын
саны бар болатын 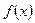 функциясы:A ) Төменнен шектелген.C)
функциясы:A ) Төменнен шектелген.C)  дан кіші болмайтын мән қабылдайтын.F) Төменнен шектелген, бірақ жоғарыдан шектелмеген.
дан кіші болмайтын мән қабылдайтын.F) Төменнен шектелген, бірақ жоғарыдан шектелмеген.
$$$ 72Координаттық жазықтық нүктелерінің кейбір ішкі жиыны қандайда бір функцияның графигі болады, егер келесі орындалса: B)  осіне параллель, кез келген түзумен бірден артық емес ортақ нүктесі болса.D)
осіне параллель, кез келген түзумен бірден артық емес ортақ нүктесі болса.D)  осіне параллель, кезкелген түзумен ортақ нүктесі болмаса.E)
осіне параллель, кезкелген түзумен ортақ нүктесі болмаса.E)  осімен бір ортақ нүктесі болса.
осімен бір ортақ нүктесі болса.
$$$ 73Функция жұп (тақ) болуы үшін, оның анықталу обласының координат басына қарағанда симметриялығы қандай шарт болып табылады: B) Қажетті.E) Міндетті шарт.G) Орын алуы тиіс.
$$$74 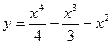 функциясы үшін кризистік нүктелер: A)
функциясы үшін кризистік нүктелер: A) 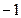 .C)
.C) 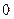 .
.
$$$ 75 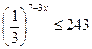 теңсіздігін қанағаттандыратын ең кіші бүтін мән: A)
теңсіздігін қанағаттандыратын ең кіші бүтін мән: A) 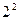 .E)
.E) 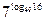 .
.
$$$ 76Теңсіздікті шешіңіз: 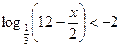 B)
B) 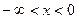 .F)
.F) 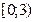 .
.
$$$ 77Функцияның кризистік нүктелерін табу алгоритмі: A) Функцияның үзіліс нүктелерін табу.B) 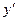 туындысын табу.C)
туындысын табу.C) 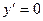 теңдеуін шешу.
теңдеуін шешу.
$$$78 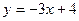 функциясының графигіне параллель және
функциясының графигіне параллель және 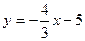 функциясының графигімен бірге ординатаның бір нүктесі арқылы өтетін сызықтық функцияның формуламен берілуі: A)
функциясының графигімен бірге ординатаның бір нүктесі арқылы өтетін сызықтық функцияның формуламен берілуі: A) 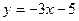 .C)
.C) 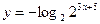 .F)
.F) 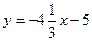 .
.
$$$79 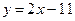 функциясының графигіне параллель және графигі
функциясының графигіне параллель және графигі 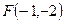 нүктесі арқылы өтетін сызықтық функцияның формуламен берілуі: A)
нүктесі арқылы өтетін сызықтық функцияның формуламен берілуі: A) 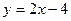 .C)
.C)  .
.
$$$80 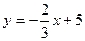 функциясының графигіне абсцисса өсіне қарағанда симметриялы болатын сызықтық функцияның формуламен берілуі:A )
функциясының графигіне абсцисса өсіне қарағанда симметриялы болатын сызықтық функцияның формуламен берілуі:A ) 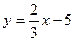 .C)
.C)  .
.
$$$ 81«Екі ондық бөлшекті қосу үшін: 1) қосылғыштардағы үтірден кейінгі таңбалар санын теңестіру; 2) үтір астында үтір болатындай, қосылғыштарды бірінің астына бірін жазу; 3) натурал сандарды қосқандай, пайда болған сандарды қосу; 4) алынған қосындыда үтірді қосылғыштардың үтірінің астына қою керек». Жоғарыдағы ережеде алгоритмнің қандай қасиеттері орындалған: A) Көлемділік және қарапайымдылық.C) Нәтижелілік.D) Дискретілігі, детерминациялық.
$$$ 82Төмендегі сабақ типтерінің қайсысы қалыпты емес сабақ типіне жатпайды: C) Жаңа материалмен таныстыру сабағы.F) Жаңа тақырып материалын бекіту сабағы.G) Білімді тексеру сабағы.
$$$ 83Төмендегі сабақ типтерінің қайсысы қалыпты емес сабақ типіне жатады: A) Интеграциялы сабақ. D) Консультация сабағы.H) Пікір талас сабағы.
$$$ 84Қалыпты емес сабақ типіне жатпайтын сабақ типі: A) Құрама сабақ.D) Жаңа материалды түсіндіру сабағы.G) Білімді жалпылау мен жүйелеу сабағы.
$$$85 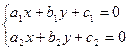 екі белгісізі бар сызықтық теңдеулер жүйесінің
екі белгісізі бар сызықтық теңдеулер жүйесінің 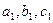 және
және 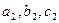 коэффициенттер арасындағы қандай қатынастарда оның жалғыз ғана шешімі болады: B)
коэффициенттер арасындағы қандай қатынастарда оның жалғыз ғана шешімі болады: B) 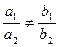 .D)
.D) 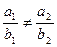 .F)
.F) 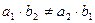 .
.
$$$86 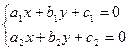 екі белгісізі бар сызықтық теңдеулер жүйесінің
екі белгісізі бар сызықтық теңдеулер жүйесінің 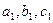 және
және 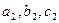 коэффициенттер арасындағы қандай қатынастарда шексіз көп шешімі болады: A)
коэффициенттер арасындағы қандай қатынастарда шексіз көп шешімі болады: A) 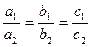 .C)
.C) 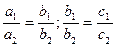 .G)
.G) 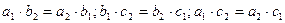 .
.
$$$87 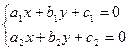 екі белгісізі бар сызықтық теңдеулер жүйесінің
екі белгісізі бар сызықтық теңдеулер жүйесінің 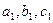 және
және 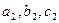 коэффициенттер арасындағы қандай қатынастарда шешімі болмайды: B)
коэффициенттер арасындағы қандай қатынастарда шешімі болмайды: B) 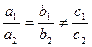 .E)
.E) 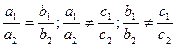 .H)
.H) 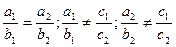 .
.
$$$ 88Тепе-теңдік болмайтын, теңдік :B) 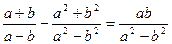 .C)
.C)  .F)
.F) 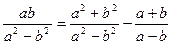 .
.
$$$ 89"Қажеттi және жеткiлiктi шарттарды" қамтитын тұжырым:A ) Егер скаляр көбейтіндісі нольге тең болса, онда екі вектор өзара перпендикуляр. B) Егер векторлар перпендикуляр болса, онда олардың скаляр көбейтіндісі нольге тең. G) Егер түзу параллель түзулердің біреуіне перпендикуляр болса, онда ол екіншісіне де перпендикуляр.
$$$90 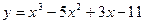 - функциясының монотонды өсу аралығы:A )
- функциясының монотонды өсу аралығы:A ) 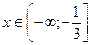 .B)
.B) 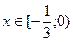 .
.
$$$ 91Шектеулілік қасиетті, функция қасиеттерінің бірімен байланыста: A) Өзгеру облысымен.E) Мәндер облысымен.G) Мәндер жиынымен.
$$$92 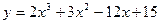 - функциясынның кему аралығы: A)
- функциясынның кему аралығы: A) 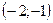 .D)
.D)  .G)
.G) 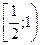 .
.
$$$93 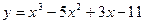 - функциясының өсу аралығы: B)
- функциясының өсу аралығы: B) 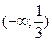 .G)
.G) 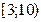 .H)
.H) 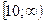 .
.
$$$ 94 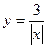 функциясының өсу аралығын табыңыз: B)
функциясының өсу аралығын табыңыз: B) 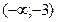 .D)
.D) 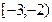 .H)
.H) 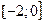 .
.
$$$95 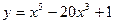 - функциясының монотонды кему аралығы:B )
- функциясының монотонды кему аралығы:B )  .F)
.F) 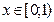 .H)
.H) 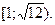
$$$ 96 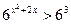 : теңсіздігінің шешімі: B)
: теңсіздігінің шешімі: B) 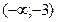 .E)
.E) 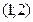 .F)
.F) 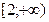 .
.






