кономическая интерпретация двойственных задач.

роверил: Герасимова А.В.

 

имитровград 2012

 

СОДЕРЖАНИЕ

Введение…………………………………………………………………………..3

Двойственная задача линейного программирования..........................................5

Симплекс-метод решения двойственной задачи линейного программирования...…………………………………………………….…….….7

Постановка задачи……………………………………………………………….16

Решение задачи…………………………………………………………………..17

Решение задачи с помощью MS excel……………………………………………...................................................19

Список используемой литературы……………………………………………..20

 

ВВЕДЕНИЕ

Математика необходима в повседневной жизни, следовательно, определенные навыки нужны каждому человеку. В жизни нам приходится считать, мы постоянно используем знания о величинах, характеризующих протяжности, площади, объемы, промежутки времени, скорости и многое другое.

Линейное программирование (ЛП) - наука о методах исследования и отыскания экстремумов линейной функции, на неизвестные величины которой наложены линейные ограничения.

То есть, задача линейного программирования, это отыскание минимального или максимального значения линейной функции с учётом системы из линейных уравнений-ограничений. Всё вместе это даёт математическую модель, какого-либо экономического процесса.

Экономико-математическая модель - это математическое описание экономического процесса или объекта. Такие модели используются для исследований и анализа экономических процессов. Реализуя их обработку на ЭВМ, мы получаем выигрыш во времени и средствах, так как проведение опытов, как правило, более трудоёмкий и дорогостоящий процесс, кроме того, не всегда возможный. Не буду здесь вдаваться в теорию моделирования, скажу лишь, что именно реализация исследования экономических процессов с помощью ЭВМ для нас и представляет интерес, а проявляется это в машинном решении задач линейного программирования, которые в свою очередь и являются экономико-математическими моделями.

Все задачи линейного программирования можно разделить на следующие группы:

· Задачи об использовании ресурсов, сырья, планирования производства

· Задачи составления рациона

· Задачи об использовании мощностей, загрузке оборудования

· Задачи о раскрое материалов

· Транспортные задачи

ДВОЙСТВЕННЫЕ ЗАДАЧИ

кономическая интерпретация двойственных задач.

Каждой задаче линейного программирования соответствует другая задача, называемая двойственной или сопряженной по отношению к исходной. Теория двойственности оказалась полезной для проведения качественных исследований задач линейного программирования.

Свойства двойственных задач:

1. В одной задаче ищут максимум линейной функции, в другой - минимум.
2. Коэффициенты при переменных в линейной функции одной задачи являются свободными членами системы ограничений в другой.
3. Каждая из задач задана в стандартной форме, причем в задаче максимизации все неравенства вида "<=", а в задаче минимизации - все неравенства вида ">=".
4. Число неравенств в системе ограничений одной задачи совпадает с числом переменных в другой задаче.
5. Условия неотрицательности переменных имеются в обеих задачах.

 

Алгоритм составлениядвойственной задачи:
1. Привести все неравенства системы ограничений исходной задачи к одному смыслу: если в исходной задаче ищут максимум линейной функции, то все неравенства системы ограничений привести к виду "<=", а если минимум - к виду ">=". Для этого неравенства, в которых данное требование не выполняется, умножить на -1.
2. Составить расширенную матрицу системы А₁ в которую включить матрицу коэффициентов при переменных А, столбец свободных членов системы ограничений и строку коэффициентов при переменных в линейной функции.
3. Найти матрицу А'₁, транспонированную к матрице А₁.
4. Сформулировать двойственную задачу на основании полученной матрицы A'₁ и условия неотрицательности переменных.

Симплексный МЕТОД РЕШЕНИЯ ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ

Геометрическая интерпретация, которой мы пользовались при решении задач линейного программирования, перестает быть пригодной для этой цели при числе свободных переменных n-m>3,а затруднительна уже при n-m=3. Для нахождения решения задачи линейного программирования в общем случае (при произвольном числе свободных переменных) применяются не геометрические, а вычислительные методы. Из них наиболее универсальным является так называемый симплекс-метод. Данный метод получил несколько различных форм (модификаций) и был разработан в 1947 году Г. Данцигом.

Допустимое множество базисных решений системы линей­ных уравнений образует в объеме многогранное тело, например тетраэдр, вершины которого угловые точки.

Каждой угловой точке многогранника решений соответствует опорный план (допустимое базисное решение).

Количество перебираемых допустимых базисных решений можно сократить и проводить не беспорядочный перебор, а по­следовательный по специальному алгоритму, улучшая значение целевой функции.

В тех случаях, когда модель содержит m уравнений, для пост­роения опорных решений используются т переменных, прини­мающих некоторые положительные значения при нулевых зна­чениях остальных свободных переменных. Вычислительная процедура может быть представлена в виде следующей последо­вательности.

Итеративный переход от одного допустимого базисного ре­шения проводится направленно от одной вершины области допу­стимых решении к другой, заключающегося в обменебазисных и свободных переменных: базисная переменная приравнивается к нулю и переходит в свободную, а соответственно свободная пере­менная переводится на место базисной. Если в столбце свобод­ных членов все элементы положительны, то решение является допустимым. Если в строке целевой функции все элементы неот­рицательные, то решение является оптимальным при решении задачи на максимум.

В соответствии с симплексным методом на первом шаге нахо­дят начальное опорное решение — допустимый вариант, удовле­творяющий всем ограничениям. Затем последовательно за опре­деленное число итераций направленно осуществляется переход от одного опорного решения к другому вплоть до оптимального. Следует заметить, что на первом шаге в качестве базисных пере­менных следует выбрать такие т переменные, каждая из которых входит только один раз в одно из т уравнений системы, при этом нет таких уравнений системы, в которые не входит ни одна из этих переменных. При этом если выбранные переменные имеют те же знаки, что и соответствующие им свободные члены в пра­вых частях, то полученное базисное решение будет допустимым. В процессе решения системы линейных уравнений необходимо ориентироваться на сохранение неотрицательности всех пере­менных, поскольку это определяет допустимость решения.

Для использования рассмотренного алгоритма симплексного метода к минимизации линейной формы связи F(X) следует ис­кать максимум функции F₁(X)=- F(X), а затем полученное реше­ние взять с обратным знаком.

Предложенный алгоритм приводит к оптимальному решению для любой модели линейного программирования за конечное число итераций, если система линейных уравнений задачи сов­местна.

Симплексный метод основан на последовательном переходе от одного базисного решения (опорного плана) задачи линейно­го программирования к другому опорному плану, при этом значе­ние целевой функции изменяется в лучшую сторону.

Идея симплекс-метода относительно проста. Пусть в задаче линейного программирования имеется n переменных и m неза­висимых линейных ограничений, заданных в форме уравнений. Мы знаем, что оптимальное решение (если оно существует) до­стигается в одной из опорных точек, где по край­ней мере k=n-m из переменных равны нулю. Выберем ка­кие-то k переменных в качестве свободных и выразим через них остальные т базисных переменных. Пусть, например, в качестве свободных выбраны первые k=n-m переменных x₁, x₂, …, x_k, а остальные т выражены через них:

(1)

Предположим, что все свободные переменные х₁, х₂,..., х_к равны нулю.

При этом мы получим:

Это решение может быть допустимым или недопустимым. Оно допустимо, если все свободные члены , неот­рицательны. Предположим, что это условие выполнено. Тогда мы получили опорное решение. Но является ли оно оптималь­ным? Чтобы проверить это, выразим целевую функцию Z через свободные переменные х₁, х₂,..., х_к:

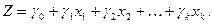(2)

Очевидно, что при х₁ = х₂ =... = х_к = 0, Z= ₀. Проверим, мо­жет ли быть улучшено решение, т. е. получено уменьшение функции Z c увеличением каких-нибудь из переменных х₁, х₂,..., х_к (уменьшать их мы не можем, так как все они равны нулю, а отрицательные значения переменных недопустимы). Если все коэффициенты , , …, в (2) положительны, то увеличение каких-либо из переменных х₁, х₂,..., х_к не может уменьшить Z; следовательно, найденное опорное решение является оптималь­ным. Если же среди коэффициентов , , …, есть отрицатель­ные, то, увеличивая некоторые из переменных х₁, х₂,..., х_к (т.е, коэффициенты при которых отрицательны), мы можем улуч­шить решение.

Пусть, например, коэффициент в (2) отрицателен. Зна­чит, есть смысл увеличить х₁ т. е. перейти от данного опорного решения к другому, где переменная х₁ не равна нулю, а вместо нее равна нулю какая-то другая. Однако увеличивать х₁ следует с осторожностью, так чтобы не стали отрицательными другие пе­ременные x_k+l, x_k+2,..., х_n, выраженные через свободные перемен­ные, в частности через x₁ формулами (1).

Например, если коэффициент при х₁ в соответствующем х_j уравнении (1) отрицателен, то увеличение x₁, может сделать х_j отрицательным. Наоборот, если среди уравнений (1) нет уравнения с отрицательным коэффициентом при x₁, то величину x₁ можно увеличивать беспредельно, а, значит, линейная функ­ция Z не ограничена снизу и оптимального решения 03 не су­ществует.

Допустим, что это не так и что среди уравнений (1) есть такие, в которых коэффициент при x₁ отрицателен. Для пере­менных, стоящих в левых частях этих уравнений, увеличение x₁ опасно — оно может сделать их отрицательными.

Возьмем одну из таких переменных x₁ и посмотрим, до какой степени можно увеличить x₁, пока переменная x₁ не станет отри­цательной. Выпишем l- еуравнение из системы (1):

Здесь свободный член 0, а коэффициент отрицателен. Легко понять, что если мы оставим х₂ = х₃ =... = х_к = 0, то х₁ можно увеличивать только до значения, равного , а при дальнейшем увеличении х₁ переменная х₁ станет отрицательной.

Выберем ту из переменных x_k+l, x_k+2,..., х_n, которая раньше всех обратится в нуль при увеличении х₁, т. е. ту, для которой ве­личина наименьшая. Пусть это будет х ₁. Тогда имеет смысл разрешить систему уравнений (1) относительно других базис­ных переменных, исключая из числа свободных переменных х ₁ и переводя вместо нее в группу свободных переменных х _r. Дейст­вительно, мы хотим перейти от опорного решения, задаваемого равенствами х₁ = х₂ =... = х_к = 0, к опорному решению, в котором уже , а х₂ =... = х_к = х_r. = 0. Первое опорное решение мы по­лучили, положив равными нулю все прежние свободные пере­менные х₁, х₂,..., х_к, второе мы получим, если обратим в нуль все новые свободные переменные х₂, х₃,..., х_к, х_r.

Базисными переменными при этом будут x₁, x_k+1, x_k+2, …, x_r-1, x_r+1, …, x_n.

Предположим, что уравнения типа (1) для нового набора базисных и свободных переменных составлены. Тогда можно выразить через новые свободные переменные и линейную функ­цию Z. Если все коэффициенты при переменных в этой формуле положительны, то мы нашли оптимальное решение: оно полу­чится, если все свободные переменные положить равными нулю. Если среди коэффициентов при переменных есть отрицатель­ные, то процедура улучшения решения продолжается: система вновь разрешается относительно других базисных переменных, и так далее, пока не будет найдено оптимальное решение, обра­щающее функцию Z в минимум.

Рассмотрим алгоритм симплексного метода на примере решения задачи пла­нирования товарооборота предприятия торговли.

Коммерческое предприятие реализует n товарных групп, рас­полагая m ограниченными материально-денежными ресурсами b_i> 0 (i=1,m). Известны расходы ресурсов каждого i -вида на ре­ализацию единицы товара по каждой группе, представленной в виде матрицы А = (a_ij), и прибыль с_ij получаемая предприятием от реализации единицы товара j -группы. Необходимо определить объем и структуру товарооборота х_j (j=1, n), при ко­торых прибыль коммерческого предприятия была бы максималь­ной.

Математическую модель задачи запишем следующим обра­зом. Определить вектор Х = (х_их₂, …,х_п), который удовлетворяет ограничениям вида:

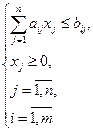
и обеспечивает максимальное значение целевой функции:

Алгоритм симплексного метода включает следующие этапы:

1. Составление первого опорного плана. Система ограничений задачи, решаемой симплексным методом, задана в виде системы неравенств смысла «<», правые части которых b_i> 0. Перейдем от системы неравенств к системе уравнений путем введения неотри­цательных дополнительных балансовых переменных. Векторы-столбцы при этих переменных представляют собой единичные векторы и образуют базис, а соответствующие им переменные называются базисными:

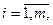
где 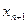- дополнительные переменные,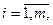

х_j- базисные переменные,

Решим эту систему относительно дополнительных перемен­ных:

,

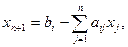
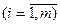а функцию цели перепишем в виде уравнения

Следует заметить, что опорным решением называется базис­ное неотрицательное решение.

Полагая, что основные переменные x₁ =х₂ =х₃ =... х_п = 0, по­лучим допустимое базисное решение - опорный план Х₁ = (0, 0,..,, 0, b_ь b₂,..., b_m); F(X₁) = 0, который заносим в симплексную таблицу. Она состоит из коэффициентов системы ограничений и свободных членов. Последняя строка таблицы называется индексной и заполняется коэффициентами функции цели, взятыми с противоположным знаком.

2. Проверка плана на оптимальность. Если значение базисных
переменных неотрицательны, то решение является допустимым.
Если все коэффициенты индексной строки симплексной табли­цы при решении задачи на максимум неотрицательны ( 0), то
план является оптимальным. Если найдется хотя бы один коэф­фициент индексной строки меньше нуля, то план не оптимальный, и его необходимо улучшить.

3. Определение ведущих столбца и строки. Из отрицательных
коэффициентов индексной строки выбираем наибольший по аб­солютной величине, что и определяет ведущий столбец, который
показывает, какая переменная на следующей итерации перейдет
из свободных в базисные.

Затем элементы столбца свободных членов симплексной таб­лицы делим на элементы того же знака (⁺/+; -/-) ведущего столб­ца. Результаты заносим в отдельный столбец Q_i, которые должны быть всегда положительны. Строка симплексной таблицы, соот­ветствующая минимальному значению Q_i, является ведущей. Она и определяет переменную x_i, которая на следующей итерации выйдет из базиса и станет свободной (обмен).

Элемент симплексной таблицы, находящийся на пересече­нии ведущих столбца и строки, называют разрешающим и выде­ляют, например, кружком.

4. Построение нового опорного плана. Переход к новому плану осуществляется в результате пересчета симплексной таблицы ме­тодом Жордана — Гаусса. Сначала заменим переменные в базисе, т.е. вместо x_i в базис войдет переменная х_j, соответствующая веду­щему столбцу (замена).

Разделим все элементы ведущей строки предыдущей симп­лексной таблицы на разрешающий элемент и результаты деления занесем в строку следующей симплексной таблицы, соответству­ющей введенной в базис переменной x_j. В результате этого на ме­сте разрешающего элемента в следующей симплексной таблице запишем 1, а в остальных клетках у столбца, включая клетку столбца индексной строки, записываем нули. Остальные новые элементы нового плана находятся по правилу прямоугольника:

,

где СТЭ - элемент старого плана;

РЭ – разрешающий элемент;

А и В – элементы старого плана, образующие прямоугольник с элементами СТЭ и РЭ.

Далее возвращаемся ко второму этапу алгоритма - проверке плана на оптимальность.

При решении задачи линейного программирования на мини­мум целевой функции признаком оптимальности плана являют­ся отрицательные значениявсех коэффициентов индексной стро­ки симплексной таблицы.

Если_в ведущем столбце все коэффициенты a_ij < 0, то функция цели F() не ограничена на множестве допустимых планов, т.е. и задача не имеет решения.

Если в столбце Q_i - симплексной таблицы содержатся два или несколько одинаковых наименьших значений, то новый опор­ный план будет вырожденным (одна или несколько базисных пе­ременных станут равными нулю). Вырожденные планы могут привести к зацикливанию, т.е. к многократному повторению процесса вычислений, не позволяющему получить оптимальный план. В таких случаях для выбора ведущей строки используют ме­тод Креко, который заключается в следующем. Элементы строк, имеющие одинаковые наименьшие значения Q_i, делятся на пред­полагаемые разрешающие элементы, а результаты заносятся в до­полнительные строки. За ведущую строку выбирается та, в кото­рой раньше встретится наименьшее частное при чтении таблицы слева направо по столбцам.

Если в оптимальный план вошла дополнительная переменная х_п+1, то при реализации такого плана имеются недоиспользован­ные ресурсы i -го вида в количестве, полученном в столбце сво­бодных членов симплексной таблицы.

Если в индексной строке симплексной таблицы оптимально­го плана находится нуль, принадлежащий свободной перемен­ной, не вошедшей в базис, а в столбце, содержащем этот нуль, имеется хотя бы один положительный элемент, то задача имеет множество оптимальных планов. Свободную переменную, соот­ветствующую указанному столбцу, можно внести в базис, выпол­нив соответствующие этапы алгоритма. В результате будет полу­чен второй оптимальный план с другим набором базисных пере­менных.

ПОСТАНОВКА ЗАДАЧИ

При откорме животных каждое из них ежедневно должно получить не менее 60 единиц питательного вещества A, не менее 50 единиц вещества B, не менее 12 единиц питательного вещества C. Указанные питательные вещества содержат 3 вида кормов. Содержание единиц питательных веществ в 1 кг каждого из видов корма приведено в таблице:

Питательные вещества	Количество единиц питательного вещества в 1 кг вида	Потребности в питательных веществах
A
B
C
Цена за 1 кг

Определить минимальные затраты при потреблении питательных веществ.

РЕШЕНИЕ ЗАДАЧИ

1.Запишем математическую модель задачи, которая удовлетворяет следующим условиям:

x₁+3x₂+4x₃≥60

2x₁+4x₂+2x₃≥50

x₁+4x₂+3x₃≥12

x_i≥0 i=1,3

И обеспечивает минимальное значение целевой функции:

F(x)= 9x₁+12x2+10x3→min

2.Составляем двойственную задачу с ограничениями:

Z(y)=60y₁+50y₂+12y₃→max

y₁+2y₂+y₃≤9

3y₁+4y₂+4y₃≤12

4y₁+2y₂+3y₃≤10

y_i≥0 i=1,3

3. Для построения первого опорного плана систему неравенств двойственной задачи приведем к системе уравнений путем введения дополнительных переменных y₄,y₅,y₆.

y₁+2y₂+y₃+y₄=9

3y₁+4y₂+4y_3+y5=12

4y₁+2y₂+3y₃₊y₆=10

y_i≥0 i=1,3

Эти переменные будут базисными.

4.Составляем симплексную таблицу(алгоритм составления описан выше):

 

 

План	Базисные переменные	Значение баз. переменных	Значение коэффициентов	Q max
Y1	Y2	Y3	Y4	Y5	Y6
	Y4
Y5
Y6								2,5
Инд. строка	Z1(y)		-60	-50	-12
	Y4	6,5		1,5	0,25			-0,25	4,33
Y5	4,5		2,5	1,75			-0,75	1,8
Y1	2,5		0,5	0,75			0,25
Инд. Строка	Z2(y)			-20
	Y4	3,8			-0,8		-0,6	0,2	4,33
Y2	1,8			0,7		0,4	-0,3	1,8
Y1	1,6			0,4		-0,2	0,4
Инд. строка	Z3(y)

 

План является оптимальным. При этом Z _max (y)=186, y₁=1,6, y₂=1,8, y₃=0

 

5. Нахождение решения прямой задачи.

На основании теоремы двойственности, которая гласит, что если одна из задач двойственной пары имеет решение, то другая также решима, можем сделать вывод:

Z _max (y)=F_min(x)=186, при этом x₁=0, x₂=8, x3=9.

Ответ: Минимальные затраты потребления питательных веществ равны 186кг.