ариант 2
1. В коробке 25 одинаковых по форме шоколадных конфет. Известно, что 15 штук из них сорта «Мишка на Севере», а остальные – сорта «Красная Шапочка». Случайным образом выбирают 3 конфеты. Вычислите вероятность того, что среди них: а) все конфеты сорта «Мишка на севере»; б) только одна конфета этого сорта; в)хотя бы одна конфета сорта «Мишка на Севере».
2. В магазин поступил одноименный товар, изготовленный двумя предприятиями. С первого предприятия поступило 150 единиц, из них 30 единиц первого сорта, а со второго предприятия 200 единиц, из них 50 первого сорта. Из общей массы товара наугад извлекается одна единица. Какова вероятность того, что она изготовлена на первом предприятии?
3. Задан закон распределения дискретной случайной величины X:
| X | –2 | –1 | |||||
| p | 0,2 | 0,31 | 0,24 | p | 0,07 | 0,04 | 0,01 |
Найти:
а) неизвестную вероятность p;
б) математическое ожидание M, дисперсию D и среднее квадратическое отклонение s данной случайной величины;
в) функцию распределения F(x) и построить её график;
г) закон распределения случайной величины Y, если её значения заданы функциональной зависимостью
y = 2x + 3.
4. Известно, что в среднем 14% стаканов, изготовляемых на данном предприятии, имеет дефект. Какова вероятность того, что из 300 стаканов данной партии: а) имеют дефект 45; б) не имеют дефекта от 230 до 250.
5. Выборка X объемом n = 100 измерений задана таблицей:
| xi | x1 | x2 | x3 | x4 | x5 | x6 | x7 |
| ni | 20 +(M+N) | 30 -(M+N) |
где xi - результаты измерений, ni - частоты, с которыми встречаются значения xi, причем 
, 
.
Необходимо: а) Построить полигон относительных частот 
.
б) Вычислить среднее выборочное 
, выборочную дисперсию Dx и среднее квадратическое отклонение σx.
в) Определить приближенно вероятность того, что наудачу выбранное измерение данной выборки X составит не менее 1,5 единиц.
г) Построить нормальную кривую (график плотности нормального распределения с найденными параметрами и σx на том же чертеже, где и полигон).
Для того, чтобы получить свои личные числовые данные, необходимо взять две последние цифры этого номера (А – предпоследняя цифра, В – последняя) и выбрать из первой таблицы параметр M, а из таблицы 2 – параметр N. Эти два числа M и N нужно подставить в условия задач контрольной работы.
Таблица 1 (выбор параметра М)
| А | ||||||||||
| M |
Таблица 2 (выбор параметра N)
| В | ||||||||||
| N |
Например, если номер зачетной книжки студента 12546, то А=4, В=6, и из таблиц находим, что М = 3 и N = 1. Полученные М = 3 и
N = 1 подставляются в условия задач контрольной работы этого студента.
ариант 3
1. В туристической группе 15 человек, среди которых только 5 человек хорошо говорят по - английски. В Лондоне группу случайным образом расселили в два отеля (3 человека и 12 человек соответственно). Вычислить вероятность того, что из членов группы в первом отеле: а) все туристы хорошо говорят по - английски; б) только один турист хорошо говорит по - английски; в) хотя бы одним турист говорит по-английски.
2. Покупатель может приобрести нужный ему товар в двух магазинах. Вероятности обращения в каждый из двух магазинов зависят от их местоположения и соответственно равны 0,3 и 0,7. Вероятность того, что к приходу покупателя нужный ему товар не будет распродан, равна 0,8 для первого магазина и 0,4 для второго. Какова вероятность того, что покупатель приобретет нужный ему товар?
3. Задан закон распределения дискретной случайной величины X:
| X | –2 | –1 | |||||
| p | 0,04 | 0,08 | 0,32 | 0,31 | 0,15 | 0,08 | p |
Найти:
а) неизвестную вероятность p;
б) математическое ожидание M, дисперсию D и среднее квадратическое отклонение s данной случайной величины;
в) функцию распределения F(x) и построить её график;
г) закон распределения случайной величины Y, если её значения заданы функциональной зависимостью y = x2 – 1.
4. Установлено, что предприятие бытового обслуживания выполняет в срок в среднем 60% заказов. Какова вероятность того, что из 150 заказов, принятых в течение некоторого времени, будут выполнены в срок:
а) ровно 90 заказов; б) от 93 до 107 заказов.
5. Выборка X объемом n = 100 измерений задана таблицей:
| xi | x1 | x2 | x3 | x4 | x5 | x6 | x7 |
| ni | 20 +(M+N) | 30 -(M+N) |
где xi - результаты измерений, ni - частоты, с которыми встречаются значения xi, причем , .
Необходимо: а) Построить полигон относительных частот .
б) Вычислить среднее выборочное , выборочную дисперсию Dx и среднее квадратическое отклонение σx.
в) Определить приближенно вероятность того, что наудачу выбранное измерение данной выборки X составит не менее 1,5 единиц.
г) Построить нормальную кривую (график плотности нормального распределения с найденными параметрами и σx на том же чертеже, где и полигон).
Для того, чтобы получить свои личные числовые данные, необходимо взять две последние цифры этого номера (А – предпоследняя цифра, В – последняя) и выбрать из первой таблицы параметр M, а из таблицы 2 – параметр N. Эти два числа M и N нужно подставить в условия задач контрольной работы.
Таблица 1 (выбор параметра М)
| А | ||||||||||
| M |
Таблица 2 (выбор параметра N)
| В | ||||||||||
| N |
Например, если номер зачетной книжки студента 12546, то А=4, В=6, и из таблиц находим, что М = 3 и N = 1. Полученные М = 3 и
N = 1 подставляются в условия задач контрольной работы этого студента.
ариант 4
1. В упаковке 12 одинаковых книг. Известно, что каждая третья книга имеет дефект обложки. Случайным образом выбирают 3 книги. Вычислите вероятность того, что среди них: а) все книги имеют дефект обложки; б) только одна книга имеет этот дефект; в) хотя бы одна книга имеет этот дефект.
2. Два контролёра производят оценку качества выпускаемых изделий. Вероятность того, что очередное изделие попадет к первому контролеру, равна 0,55; ко второму контролеру – 0,45. Первый контролёр выявляет дефект с вероятностью 0,8, а второй – с вероятностью 0,9. Вычислите вероятность того, что изделие с дефектом будет признано годным к эксплуатации.
3. Задан закон распределения дискретной случайной величины X:
| X | –2 | –1 | |||||
| p | 0,42 | 0,23 | p | 0,10 | 0,06 | 0,03 | 0,01 |
Найти:
а) неизвестную вероятность p;
б) математическое ожидание M, дисперсию D и среднее квадратическое отклонение s данной случайной величины;
в) функцию распределения F(x) и построить её график;
г) закон распределения случайной величины Y, если её значения заданы функциональной зависимостью y = - 2 x + 1.
4. Известно, что в данном технологическом процессе 10% изделий имеют дефект. Какова вероятность того, что в партии из 400 изделий:
а) не будут иметь дефекта 342 изделия;
б) будут иметь дефект от 30 до 52 изделий.
5. Выборка X объемом n = 100 измерений задана таблицей:
| xi | x1 | x2 | x3 | x4 | x5 | x6 | x7 |
| ni | 20 +(M+N) | 30 -(M+N) |
где xi - результаты измерений, ni - частоты, с которыми встречаются значения xi, причем , .
Необходимо: а) Построить полигон относительных частот .
б) Вычислить среднее выборочное , выборочную дисперсию Dx и среднее квадратическое отклонение σx.
в) Определить приближенно вероятность того, что наудачу выбранное измерение данной выборки X составит не менее 1,5 единиц.
г) Построить нормальную кривую (график плотности нормального распределения с найденными параметрами и σx на том же чертеже, где и полигон).
Для того, чтобы получить свои личные числовые данные, необходимо взять две последние цифры этого номера (А – предпоследняя цифра, В – последняя) и выбрать из первой таблицы параметр M, а из таблицы 2 – параметр N. Эти два числа M и N нужно подставить в условия задач контрольной работы.
Таблица 1 (выбор параметра М)
| А | ||||||||||
| M |
Таблица 2 (выбор параметра N)
| В | ||||||||||
| N |
Например, если номер зачетной книжки студента 12546, то А=4, В=6, и из таблиц находим, что М = 3 и N = 1. Полученные М = 3 и
N = 1 подставляются в условия задач контрольной работы этого студента.
ариант 5
1. К экзамену приготовлено 24 одинаковых ручки. Известно, что треть из них имеет фиолетовый стержень, остальные – синий стержень. Случайным образом отбирают три ручки. Вычислить вероятность того, что:
а) все ручки имеют фиолетовый стержень; б) только одна ручка имеет фиолетовый стержень; в) хотя бы одна ручка имеет фиолетовый стержень.
2. Пассажир может приобрести билет в одной из двух касс. Вероятность обращения в первую кассу составляет 0,4, а во вторую – 0,6. Вероятность того, что к моменту приходя пассажира нужные ему билеты будут распроданы, равна 0,35 для первой кассы и 0,7 для второй. Пассажир посетил одну из касс и приобрел билет. Какова вероятность того, что он приобрел его во второй кассе?
3. Задан закон распределения дискретной случайной величины X:
| X | –2 | –1 | |||||
| p | p | 0,29 | 0,12 | 0,15 | 0,21 | 0,16 | 0,04 |
Найти:
а) неизвестную вероятность p;
б) математическое ожидание M, дисперсию D и среднее квадратическое отклонение s данной случайной величины;
в) функцию распределения F(x) и построить её график;
г) закон распределения случайной величины Y, если её значения заданы функциональной зависимостью y = ½ x ½.
4. По данным телеателье установлено, что в среднем 20% цветных телевизоров выходят из строя в течение гарантийного срока. Какова вероятность того, что из 225 проданных цветных телевизоров будут работать исправно в течение гарантийного срока: а) 164 телевизора; б) от 172 до 184 телевизоров.
5. Выборка X объемом n = 100 измерений задана таблицей:
| xi | x1 | x2 | x3 | x4 | x5 | x6 | x7 |
| ni | 20 +(M+N) | 30 -(M+N) |
где xi - результаты измерений, ni - частоты, с которыми встречаются значения xi, причем , .
Необходимо: а) Построить полигон относительных частот .
б) Вычислить среднее выборочное , выборочную дисперсию Dx и среднее квадратическое отклонение σx.
в) Определить приближенно вероятность того, что наудачу выбранное измерение данной выборки X составит не менее 1,5 единиц.
г) Построить нормальную кривую (график плотности нормального распределения с найденными параметрами и σx на том же чертеже, где и полигон).
Для того, чтобы получить свои личные числовые данные, необходимо взять две последние цифры этого номера (А – предпоследняя цифра, В – последняя) и выбрать из первой таблицы параметр M, а из таблицы 2 – параметр N. Эти два числа M и N нужно подставить в условия задач контрольной работы.
Таблица 1 (выбор параметра М)
| А | ||||||||||
| M |
Таблица 2 (выбор параметра N)
| В | ||||||||||
| N |
Например, если номер зачетной книжки студента 12546, то А=4, В=6, и из таблиц находим, что М = 3 и N = 1. Полученные М = 3 и
N = 1 подставляются в условия задач контрольной работы этого студента.
ариант 6
1. В нижней палате парламента 40 депутатов, среди которых первая партия имеет 20 представителей, вторая – 12 представителей, третья 5 представителей, а остальные считают себя независимыми. Случайным образом выбирают трех депутатов. Вычислите вероятность того, что среди них:
а) только представители первой партии, б) только один депутат из первой партии; в) хотя бы один депутат из первой партии.
2. Два специалиста ОТК проверяют качество выпускаемых изделий, причем каждое изделие с одинаковой вероятностью может быть проверено любым из них. Вероятность выявления дефекта первым специалистом равна 0,8, а вторым 0,9. Из массы проверенных изделий наугад выбрано одно, оно оказалось с дефектом. Какова вероятность того, что ошибку допустил второй контролер?
3. Задан закон распределения дискретной случайной величины X:
| X | -2 | -1 | |||||
| p | 0,05 | 0,12 | 0,18 | 0,30 | p | 0,12 | 0,05 |
Найти:
а) неизвестную вероятность p;
б) математическое ожидание M, дисперсию D и среднее квадратическое отклонение s данной случайной величины;
в) функцию распределения F(x) и построить её график;
г) закон распределения случайной величины Y, если её значения заданы функциональной зависимостью y =5x - 2.
4. При оценке качества продукции было установлено, что в среднем третья часть выпускаемой фабрикой обуви имеет различные дефекты отделки. Какова вероятность того, что в партии из 200 пар, поступившей в магазин:
а) будут иметь дефекты отделки 60 пар;
б) не будут иметь дефектов отделки от 120 до 148 пар.
5. Выборка X объемом n = 100 измерений задана таблицей:
| xi | x1 | x2 | x3 | x4 | x5 | x6 | x7 |
| ni | 20 +(M+N) | 30 -(M+N) |
где xi - результаты измерений, ni - частоты, с которыми встречаются значения xi, причем , .
Необходимо: а) Построить полигон относительных частот .
б) Вычислить среднее выборочное , выборочную дисперсию Dx и среднее квадратическое отклонение σx.
в) Определить приближенно вероятность того, что наудачу выбранное измерение данной выборки X составит не менее 1,5 единиц.
г) Построить нормальную кривую (график плотности нормального распределения с найденными параметрами и σx на том же чертеже, где и полигон).
Для того, чтобы получить свои личные числовые данные, необходимо взять две последние цифры этого номера (А – предпоследняя цифра, В – последняя) и выбрать из первой таблицы параметр M, а из таблицы 2 – параметр N. Эти два числа M и N нужно подставить в условия задач контрольной работы.
Таблица 1 (выбор параметра М)
| А | ||||||||||
| M |
Таблица 2 (выбор параметра N)
| В | ||||||||||
| N |
Например, если номер зачетной книжки студента 12546, то А=4, В=6, и из таблиц находим, что М = 3 и N = 1. Полученные М = 3 и
N = 1 подставляются в условия задач контрольной работы этого студента.
Вариант 7
1. В ящике 18 одинаковых бутылок пива без этикеток. Известно, что треть из них «Жигулевское». Случайным образом выбирают 3 бутылки. Вычислите вероятность того, что среди них: а) только пиво сорта «Жигулевское»; б) ровно одна бутылка этого сорта; в) хотя бы одна бутылка этого сорта.
2. В двух одинаковых коробках находятся карандаши “Конструктор”. Известно, что треть карандашей в первой коробке и ¼ во второй имеют твердость ТМ. Наугад выбирается коробка, из нее наугад извлекается один карандаш. Он оказывается твердости ТМ. Какова вероятность того, что он извлечен из первой коробки?
3. Задан закон распределения дискретной случайной величины X:
| X | -2 | -1 | |||||
| p | 0,16 | 0,25 | 0,25 | 0,16 | 0,10 | p | 0,03 |
Найти:
а) неизвестную вероятность p;
б) математическое ожидание M, дисперсию D и среднее квадратическое отклонение s данной случайной величины;
в) функцию распределения F(x) и построить её график;
г) закон распределения случайной величины Y, если её значения заданы функциональной зависимостью
y = 4½ x ½ - 1.
4. Известно, что вероятность рождения мальчика равна 0,51, а девочки 0,49. Какова вероятность того, что 300 новорожденных окажется:
а) 150 мальчиков; б) от 150 до 200 мальчиков?
5. Выборка X объемом n = 100 измерений задана таблицей:
| xi | x1 | x2 | x3 | x4 | x5 | x6 | x7 |
| ni | 20 +(M+N) | 30 -(M+N) |
где xi - результаты измерений, ni - частоты, с которыми встречаются значения xi, причем , .
Необходимо: а) Построить полигон относительных частот .
б) Вычислить среднее выборочное , выборочную дисперсию Dx и среднее квадратическое отклонение σx.
в) Определить приближенно вероятность того, что наудачу выбранное измерение данной выборки X составит не менее 1,5 единиц.
г) Построить нормальную кривую (график плотности нормального распределения с найденными параметрами и σx на том же чертеже, где и полигон).
Для того, чтобы получить свои личные числовые данные, необходимо взять две последние цифры этого номера (А – предпоследняя цифра, В – последняя) и выбрать из первой таблицы параметр M, а из таблицы 2 – параметр N. Эти два числа M и N нужно подставить в условия задач контрольной работы.
Таблица 1 (выбор параметра М)
| А | ||||||||||
| M |
Таблица 2 (выбор параметра N)
| В | ||||||||||
| N |
Например, если номер зачетной книжки студента 12546, то А=4, В=6, и из таблиц находим, что М = 3 и N = 1. Полученные М = 3 и
N = 1 подставляются в условия задач контрольной работы этого студента.
ариант 8
1. В студенческой группе 20 девушек. Известно, что 5 из них не любят читать детективы. Случайным образом выбирают трех девушек и дарят им по детективу. Вычислите вероятность того, что: а) все девушки оценят этот подарок; б) только одна девушка оценит этот подарок; в) хотя бы одна девушка оценит этот подарок.
2. Товаровед плодоовощной базы определяет сорт поступившей от постоянного поставщика партии яблок. Известно, что в среднем 40% выращенного поставщиком урожая составляют яблоки первого сорта. Вероятность того, что товаровед признает первосортную партию первым сортом, равна 0,85. Кроме того, он может допустить ошибку, сочтя непервосортную партию первосортной, с вероятностью 0,2. Какова вероятность того, что он неверно установит сорт партии яблок?
3. Задан закон распределения дискретной случайной величины X:
| X | -2 | -1 | |||||
| p | 0,06 | p | 0,12 | 0,24 | 0,33 | 0,14 | 0,03 |
Найти:
а) неизвестную вероятность p;
б) математическое ожидание M, дисперсию D и среднее квадратическое отклонение s данной случайной величины;
в) функцию распределения F(x) и построить её график;
г) закон распределения случайной величины Y, если её значения заданы функциональной зависимостью y = x2+2.
4. Вероятность нормального расхода электроэнергии за день на предприятии бытового обслуживания равна 0,7. Какова вероятность того, что из 90 дней предприятие нормально расходует электроэнергию: а) в течение 60 дней; б) от 60 до 90 дней?
5. Выборка X объемом n = 100 измерений задана таблицей:
| xi | x1 | x2 | x3 | x4 | x5 | x6 | x7 |
| ni | 20 +(M+N) | 30 -(M+N) |
где xi - результаты измерений, ni - частоты, с которыми встречаются значения xi, причем , .
Необходимо: а) Построить полигон относительных частот .
б) Вычислить среднее выборочное , выборочную дисперсию Dx и среднее квадратическое отклонение σx.
в) Определить приближенно вероятность того, что наудачу выбранное измерение данной выборки X составит не менее 1,5 единиц.
г) Построить нормальную кривую (график плотности нормального распределения с найденными параметрами и σx на том же чертеже, где и полигон).
Для того, чтобы получить свои личные числовые данные, необходимо взять две последние цифры этого номера (А – предпоследняя цифра, В – последняя) и выбрать из первой таблицы параметр M, а из таблицы 2 – параметр N. Эти два числа M и N нужно подставить в условия задач контрольной работы.
Таблица 1 (выбор параметра М)
| А | ||||||||||
| M |
Таблица 2 (выбор параметра N)
| В | ||||||||||
| N |
Например, если номер зачетной книжки студента 12546, то А=4, В=6, и из таблиц находим, что М = 3 и N = 1. Полученные М = 3 и
N = 1 подставляются в условия задач контрольной работы этого студента.
ариант 9
1. В коробке 30 одинаковых юбилейных монет. Известно, что 5 из них имеют нестандартный процент содержания золота. Случайным образом выбирают три монеты. Вычислите вероятность того, что: а) все монеты имеют нестандартный процент содержания золота; б) только одна монета имеет нестандартный процент содержания золота; в) хотя бы одна монета имеет нестандартный процент содержания золота.
2. Магазин получил две равные по количеству партии одноименного товара. Известно что 25% первой партии и 40% второй партии составляет товар первого сорта. Какова вероятность того, что наугад выбранная единица товара будет не первого сорта?
3. Задан закон распределения дискретной случайной величины X:
| X | -2 | -1 | |||||
| p | 0,02 | 0,38 | 0,30 | p | 0,08 | 0,04 | 0,02 |
Найти:
а) неизвестную вероятность p;
б) математическое ожидание M, дисперсию D и среднее квадратическое отклонение s данной случайной величины;
в) функцию распределения F(x) и построить её график;
г) закон распределения случайной величины Y, если её значения заданы функциональной зависимостью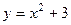 
.
4. Известно, что вероятность опоздания ежедневного поезда на станцию равна 0,2. Какова вероятность того, что в течение 200 дней поезд опоздает на станцию а) 50 раз; б) от 100 до 150 раз?
5. Выборка X объемом n = 100 измерений задана таблицей:
| xi | x1 | x2 | x3 | x4 | x5 | x6 | x7 |
| ni | 20 +(M+N) | 30 -(M+N) |
где xi - результаты измерений, ni - частоты, с которыми встречаются значения xi, причем , .
Необходимо: а) Построить полигон относительных частот .
б) Вычислить среднее выборочное , выборочную дисперсию Dx и среднее квадратическое отклонение σx.
в) Определить приближенно вероятность того, что наудачу выбранное измерение данной выборки X составит не менее 1,5 единиц.
г) Построить нормальную кривую (график плотности нормального распределения с найденными параметрами и σx на том же чертеже, где и полигон).
Для того, чтобы получить свои личные числовые данные, необходимо взять две последние цифры этого номера (А – предпоследняя цифра, В – последняя) и выбрать из первой таблицы параметр M, а из таблицы 2 – параметр N. Эти два числа M и N нужно подставить в условия задач контрольной работы.
Таблица 1 (выбор параметра М)
| А | ||||||||||
| M |
Таблица 2 (выбор параметра N)
| В | ||||||||||
| N |
Например, если номер зачетной книжки студента 12546, то А=4, В=6, и из таблиц находим, что М = 3 и N = 1. Полученные М = 3 и
N = 1 подставляются в условия задач контрольной работы этого студента.
ариант 10
1. На витрине 32 одинаковых булочки. Известно, что среди них четверть булочек с изюмом, остальные с корицей. Случайным образом отбирают три булочки. Вычислите вероятность того, что: а) все выбранные булочки с изюмом; б) только одна булочка с изюмом; в) хотя бы одна булочка с изюмом.
2. Укупорка банок производится двумя автоматами с одинаковой производительностью. Доля банок с дефектом укупорки для первого автомата составляет 1%, а для второго 0,5%. Какова вероятность того, что наугад взятая банка будет иметь дефект укупорки?
3. Задан закон распределения дискретной случайной величины X:
| X | -2 | -1 | |||||
| p | 0,08 | 0,10 | 0,14 | 0,17 | 0,19 | 0,18 | p |
Найти:
а) неизвестную вероятность p;
б) математическое ожидание M, дисперсию D и среднее квадратическое отклонение s данной случайной величины;
в) функцию распределения F(x) и построить её график;
г) закон распределения случайной величины Y, если её значения заданы функциональной зависимостью 
4. Установлено, что третья часть покупателей при посещении модного магазина приобретает себе одежду. Какова вероятность того, что из 150 посетителей магазина: а) ровно 50 человек приобретут товар; б) от 100 до 120 человек приобретут товар?
5. Выборка X объемом n = 100 измерений задана таблицей:
| xi | x1 | x2 | x3 | x4 | x5 | x6 | x7 |
| ni | 20 +(M+N) | 30 -(M+N) |
где xi - результаты измерений, ni - частоты, с которыми встречаются значения xi, причем , .
Необходимо: а) Построить полигон относительных частот .
б) Вычислить среднее выборочное , выборочную дисперсию Dx и среднее квадратическое отклонение σx.
в) Определить приближенно вероятность того, что наудачу выбранное измерение данной выборки X составит не менее 1,5 единиц.
г) Построить нормальную кривую (график плотности нормального распределения с найденными параметрами и σx на том же чертеже, где и полигон).
Для того, чтобы получить свои личные числовые данные, необходимо взять две последние цифры этого номера (А – предпоследняя цифра, В – последняя) и выбрать из первой таблицы параметр M, а из таблицы 2 – параметр N. Эти два числа M и N нужно подставить в условия задач контрольной работы.
Таблица 1 (выбор параметра М)
| А | ||||||||||
| M |
Таблица 2 (выбор параметра N)
| В | ||||||||||
| N |
Например, если номер зачетной книжки студента 12546, то А=4, В=6, и из таблиц находим, что М = 3 и N = 1. Полученные М = 3 и
N = 1 подставляются в условия задач контрольной работы этого студента.
писок рекомендуемой литературы.
Основная литература
1. Кремер, Н.Ш. Теория вероятностей и математическая
статистика 
: учебник для студентов вузов, обучающихся по экономическим специальностям / Н.Ш.Кремер – 3-е изд.,перераб. и доп. – М.: ЮНИТИ–Дана, 2007
2. Гмурман, В.Е. Теория вероятностей и математическая
статистика : учебное пособие. – 12-е изд., перераб.– М.: Высшее образование, 2008
3. Колемаев, В.А. Теория вероятностей и математическая
статистика : учебник / В.А. Колемаев, В.Н. Калинина; под ред. В.А. Колемаева.– 2-е изд., перераб. и доп. – М.: ЮНИТИ, 2003
4. Общий курс высшей математики для экономистов
: учебник / под ред. В.И. Ермакова – М.: ИНФРА-М., 2007
5. Сборник задач по высшей математике для экономистов
: учебное пособие / под ред. В.И. Ермакова – М.: ИНФРА-М,2002
6. Гмурман, В.Е. Руководство к решению задач по теории вероятностей и математической статистике : учеб.пособие / Гмурман В.Е. – 11-е изд., перераб.– М.: Высшее образование, 2008
Дополнительная литература
7. Красс, М.С., Чупрынов, Б.П. Математика для экономис-
тов серия «учеб.пособие» – СПб.: Питер, 2007
8. Письменный, Д.Т. Конспект лекций по теории вероят-
ностей, математической статистике и случайным процессам : / Д.Письменный. – 2-е изд. – М.: Айрис-пресс, 2007
9. Шапкин, А.С. Задачи по высшей математике, теории
вероятностей, математической статистике, математическому программированию с решениями: учеб.пособие. – 5-е изд. М.: Издательско-торговая корпорация «Дашков и К», 2008
10. Золотаревская, Д.И. Теория вероятностей. Задачи с
решениями: учеб.пособие. – Изд.5-е. М.: изд. ЛКИ, 2007
11. Данко, П.Е. Высшая математика в упражнениях и
задачах. В 2 ч. Ч.2: учеб.пособие для вузов / П.Е. Данко, А.Г. Попов, Т.Я. Кожевникова, С.П. Данко – 6-е изд. – М.: ООО»Изд.Оникс»: ООО изд. «Мир и образование», 2007
12. Справочник по математике для экономистов: учеб.пособие / под ред.проф. В.И. Ермакова. – 3-е изд., перераб. и доп. – М.: ИНФРА-М, 2007
Учебно-методическая литература
13. Авдонькина, А.В., Писаренко, И.В., Самаров, А.Б.
Математика: раздел «Теория вероятностей», учеб.пособие для студ.I курса экономических специальностей. – Челябинск, Челябинский институт (филиал) РГТЭУ, 2010 (Электронный вариант)
14. Авдонькина, А.В., Математика Часть 2: Метод. реко-
мендации, инд. и контр.задания для самостоятельной работы / А.В. Авдонькина, В.Н. Ни – Челябинск: Челябинский институт (филиал) ГОУ ВПО «РГТЭУ», 2007
15. Авдонькина, А.В., Ни В.Н. Методические указания к проведению практических занятий по теории вероятностей. Челябинск: ЧИ МГУК, 1999
16. Авдонькина, А.В., Писаренко, И.В. Методические рекомендации по разделу «Математическая статистика», – Челябинск: Челябинский институт (филиал) РГТЭУ, 2010 (Электронный вариант)
