МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ ДОНСКОЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
(ДГТУ)
КАФЕДРА «МАТЕМАТИКА»
КОНТРОЛЬНАЯ РАБОТА № 1 ДЛЯ СТУДЕНТОВ
ЗАОЧНОЙ ФОРМЫ ОБУЧЕНИЯ
ТЕХНИЧЕСКИХ НАПРАВЛЕНИЙ
Ростов-на-Дону 2014
Составители: Волокитин Г.И., Ступникова Н.П.
Программа и варианты контрольной работы № 1 для студентов первого курса заочного формы обучения: Методические указания / ДГТУ. Ростов н/Д: Издательский центр ДГТУ, 2014. – с.
Методическая разработка предназначена для студентов заочной формы обучения технических направлений. Содержит программу курса математики по темам: «Линейная алгебра», «Векторная алгебра и аналитическая геометрия». Указана рекомендуемая литература, варианты контрольной работы № 1 (первый семестр), а также даны образцы решения задач. Номер варианта студент определяет по последней цифре зачетной книжки.
Рецензент: к.ф.-м.н., доц. Ворович Е.И. (ДГТУ, г. Ростов-на-Дону)
Научный редактор: д.ф.-м.н., проф. Ларченко В.В.
© Издательский центр ДГТУ, 2014
Экзаменационная программа по математике
Для студентов 1-го курса заочного факультета.
Элементы линейной алгебры.
Матрицы, виды матриц и действия с матрицами. Числовые характеристики матриц. Определители второго и третьего порядков: определения, свойства и способы вычисления. Элементарные преобразования матриц. Обратная матрица: определение, критерий существования и способы вычисления обратной матрицы. Базисный минор и ранг матрицы. Системы линейны алгебраических уравнений, их виды. Теорема Кронекера-Капелли. Решение определенных систем третьего порядка методом Крамера, матричным методом и методом Гаусса. Общее решение однородных и неоднородных неопределенных систем. Понятие линейного пространства. Линейный оператор, матрица линейного оператора.
Векторная алгебра и аналитическая геометрия.
Понятие геометрического вектора. Проекция вектора на ось. Линейные операции над векторами. Линейная независимость векторов, базис на плоскости и в пространстве. Координаты вектора, их геометрический смысл. Действия с векторами в координатах. Условие коллинеарности векторов. Скалярное произведение двух векторов: определение, свойства, вычисление в координатах и приложения. Векторное произведение двух векторов: определение, свойства, вычисление в координатах и приложения. Смешанное произведение трех векторов, теорема о геометрическом смысле, вычисление в координатах и свойства. Условие компланарности трех векторов.
Прямая на плоскости. Угловой коэффициент прямой. Различные виды уравнений прямой (каноническое уравнение, общее, «в отрезках», нормальное). Угол между прямыми. Расстояние от точки до прямой.
Плоскость: нормальный вектор, общее уравнение плоскости. Различные виды уравнений плоскости («в отрезках», нормальное уравнение). Угол между плоскостями, расстояние от точки до плоскости.
Прямая в пространстве: канонические, параметрические уравнения. Прямая как пересечение двух плоскостей. Угол между прямыми и угол между прямой и плоскостью.
Системы координат на плоскости: прямоугольная и полярная. Системы координат в пространстве: прямоугольная, цилиндрическая и сферическая. Кривые второго порядка: определения и канонические уравнения эллипса, окружности, гиперболы и параболы. Поверхности второго порядка: Эллипсоиды, сфера, однополостный и двуполостный гиперболоиды, эллиптический и гиперболический параболоиды. Конус второго порядка. Цилиндры второго порядка.
Литература:
1. Беклемишев Д.В. Курс аналитической геометрии и линейной алгебры. -М.: Наука, 1984.
2. Данко П.В., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. – М.: Высшая школа, 1986.
3. Волокитин Г.И., Ларченко В.В., Азаров Д.А., Редько Ю.С. Начала линейной алгебры. Учебное пособие. – Ростов-на-Дону: Издательский центр ДГТУ, 2012.
4. Я.С. Бугров, С.М. Никольский. Элементы линейной алгебры и аналитическая геометрия. Москва «Наука». Главная редакция физико-математической литературы, 1980.
5. В.А. Ильин, Э.Г. Позняк. Аналитическая геометрия. Издание четвертое, дополненное. Москва «Наука» Главная редакция физико-математической литературы, 1973.
ВАРИАНТЫ ЗАДАНИЙ КОНТРОЛЬНОЙ РАБОТЫ № 1
Задача 1. Даны матрицы 
и 
. 
- единичная матрица. Найти:
а) матрицу 
; б) обратную матрицу 
и проверить, что 
:
1. 
; 2. 
;
3. 
; 4. 
;
5. 
; 6. 
;
7. 
; 8. 
;
9. 
; 10. 
.
Задача 2. Тремя методами (Крамера, матричным методом и методом Гаусса) решить систему линейных алгебраических уравнений: 
, где матрицы и заданы в условии задачи 1, а 
- матрица-столбец неизвестных 
.
Задача 3. Даны точки
. Найти:
а). Координаты, модуль и направляющие косинусы вектора 
;
б). Проекцию вектора на вектор 
;
в).Скалярное произведение векторов и 
, а также угол между ними;
г).Векторное произведение векторов и 
, а также площадь треугольника 
;
д). Смешанное произведение векторов 
, а также объем пирамиды ABCD.
1. 
;
2. 
;
3. 
;
4. 
;
5. 
;
6. 
;
7. 
;
8. 
;
9. 
;
10. 
.
Задача 4. На плоскости даны вершины треугольника . Найти:
а). Канонические уравнения сторон 
и 
;
б). Уравнение высоты, опущенной из вершины B;
в). Внутренний угол 
;
г). Уравнение медианы, проведенной из вершины B;
д). Расстояние от точки В до стороны . Сделать чертеж:
1. 
;
2. 
;
3. 
;
4. 
;
5. 
;
6. 
;
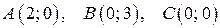7. 
;
8. 
;
9. 
;
10. 
.
Задача 5. Точки , , 
, 
, координаты которых заданы в условии задачи 3, являются вершинами пирамиды. Найти:
а). Уравнения ребра ;
б). Угол между ребрами и ;
в). Уравнение грани 
;
г). Угол между ребром 
и гранью ;
д). Уравнение высоты пирамиды, опущенной из вершины , а также проекцию этой вершины на плоскость .
ОБРАЗЦЫ РЕШЕНИЯ ЗАДАЧ КОНТРОЛЬНОЙ РАБОТЫ №1
Пример 1. Даны матрицы и . - единичная матрица. Найти:
а) матрицу ; б) обратную матрицу и проверить, что :
.
Решение. а). Раскроем скобки, получим
.
Применяя правило умножения матрицы на матрицу, имеем
.
Следовательно,
.
б). Обратную матрицу 
найдем, используя присоединенную матрицу 
. Элементы присоединенной матрицы - это алгебраические дополнения соответствующих элементов матрицы , расположенные по столбцам:
.
Обратная матрица определяется формулой:
.
Вычислим определитель матрицы, проверим, что матрица невырожденная, следовательно, имеет обратную матрицу. Определитель найдем, раскрывая по элементам первой строки:
.
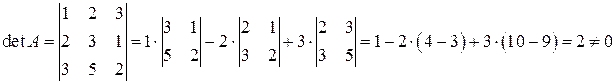Находим алгебраические дополнения элементов исходной матрицы :
.
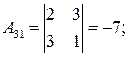
Итак, присоединенная матрица имеет вид:
.
Таким образом, обратная матрица равна
.
Проверим, что обратная матрица найдена правильно, должно выполняться условие . Вычислим элементы произведения матриц:
- верно,
- верно,
- верно.
Пример 2. Тремя методами (Крамера, матричным методом и методом Гаусса) решить систему линейных алгебраических уравнений: , где матрицы и заданы в условии задачи 1, а - матрица-столбец неизвестных .
Решение. Учитывая правило перемножения матриц, запишем подробный вид системы:
.
Получим решение по формулам Крамера: 
. Здесь 
- определитель матрицы системы, он найден в задаче 1 при нахождении обратной матрицы. 
- определители, полученные из определителя матрицы системы заменой соответственно первого, второго, третьего столбца матрицы столбцом правых частей:
.
Таким образом, получаем,
.
Получим решение матричным методом. В этом случае решение определяется формулой:
.
Обратная матрица была найдена при решении задачи 1. Поэтому сразу запишем
.
Сравнивая соответствующие элементы матриц слева и справа, снова находим
.
Получим решение методом Гаусса. При помощи элементарных преобразований строк расширенной матрицы 
последовательно исключаем неизвестные в уравнениях системы. На месте клетки получим единичную матрицу , при этом на месте клетки появится вектор решения.
. Итак, 
.
Пример 3. Даны точки
. Найти:
а). Координаты, модуль и направляющие косинусы вектора ;
б). Проекцию вектора на вектор ;
в).Скалярное произведение векторов и , а также угол между ними;
г).Векторное произведение векторов и , а также площадь треугольника ;
д). Смешанное произведение векторов , а также объем пирамиды ABCD.
Решение. а) Вектор найдем по формуле 
: 
. Модуль вектора 
определяется соотношением 
. Получаем отсюда 
. Направляющие косинусы – это координаты орта вектора . Т.е. вектора 
. Направляющие косинусы равны: 
.
б). Проекцию вектора вычислим с помощью скалярного произведения:
.
Найдем вектор 
. Учитывая формулу вычисления скалярного произведения векторов в координатах
,
найдем проекцию
.
в). Найдем вектор и вычислим скалярное произведение векторов и . 
. 
.
Косинус угла 
между векторами и определяется равенством
.
Отсюда заключаем, что угол 
.
Найдем вектор и вычислим векторное произведение векторов с помощью формулы
.
. 
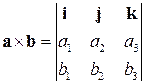. Учитывая, что модуль векторного произведения – площадь параллелограмма, для площади треугольника имеем соотношение
.
д). Найдем вектор 
и вычислим смешанное произведение по формуле
.
Имеем 
. 
.
Учитывая, что модуль смешанного произведения численно равен объему параллелепипеда, построенного па векторах-сомножителях, а объем пирамиды составляет шестую часть объема параллелепипеда, получаем
.
Пример 4.. На плоскости даны вершины треугольника . Найти:
а). Канонические уравнения сторон и ;
б). Уравнение высоты, опущенной из вершины B;
в). Внутренний угол ;
г). Уравнение медианы, проведенной из вершины B;
д). Расстояние от точки В до стороны . Сделать чертеж:
.
Решение. а). Уравнения сторон найдем, используя уравнение прямой, проходящей через две заданные точки: 
.
Угловой коэффициент прямой равен 
.
б). Угловой коэффициент высоты 
связан с угловым коэффициентом стороны соотношением 
. Отсюда находим, 
. Уравнение высоты составим, используя уравнение прямой, имеющей заданный наклон и проходящей через заданную точку: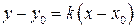 
.
.
в). Для нахождения внутреннего угла используем формулу
.
Получаем, 
. 
.
г). Чтобы составить уравнение медианы, найдем координаты точки 
- середины стороны : 
.
(каноническое уравнение вертикальной прямой).
д). Расстояние от вершины до стороны найдем по формуле:
, где 
- общее уравнение прямой, 
-
точка, от которой определяется расстояние. Общее уравнение стороны имеет вид: 
. Поэтому 
.
Строим треугольник в координатных осях:
Пример 5. Точки 
являются вершинами пирамиды. Найти:
а). Уравнения ребра ;
б). Угол между ребрами и ;
в). Уравнение грани ;
г). Угол между ребром и гранью ;
д). Уравнение высоты пирамиды, опущенной из вершины , а также проекцию этой вершины на плоскость .
Решение. а). Канонические уравнения прямой в пространстве, проходящей через две заданные точки, определяются соотношениями
.
Следовательно, уравнения ребра имеют вид
, или 
.
б). Угол между ребрами - это угол между векторами и .
Эти векторы соответственно равны 
и 
. Поэтому
.
в). Составим уравнение грани , используя условие компланарности векторов , и текущего вектора 
:
.
Раскрывая определитель, получим
, или
.
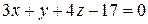г). Угол 
между прямой с направляющим вектором 
и плоскостью с нормальным вектором 
определяется формулой
.
Направляющий вектор ребра равен 
, координаты нормального вектора плоскости – это коэффициенты в общем уравнении плоскости, т.е. 
. Отсюда получаем
, 
.
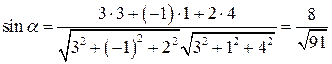д). Направляющим вектором высоты пирамиды, опущенной из вершины , является нормальный вектор плоскости . Поэтому канонические уравнения высоты следующие
.
Проекцию 
вершины на плоскость основания найдем как пересечение прямой 
и плоскости . Для этого от канонических уравнений высоты перейдем к параметрическим уравнениям:
Подставляя последние соотношения в уравнение плоскости , получаем уравнение для определения значения параметра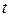 
, соответствующего точке :
.
Подставляя полученное значение 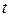в параметрические уравнения высоты, находим координаты точки :
.
