1. Для выполнения этого задания[1]необходимо изучить материал лекций и [1,4,7,8].
2. При построении графика и вычислении значения функции Y каждого варианта рекомендуется в качестве аргумента х использовать номер рассматриваемого периода. Например, если временной интервал - это годы 1999, 2000,..., 2005, то 1999 году соответствует период 1, 2000 году – период 2, 2005 году – период 7 и т.д.Для вычисления значения функции Y в указанном периоде рекомендуется задать эту функцию с использованием функционального оператора ->, затем обратиться к ней для конкретных значений аргумента [8, стр.50].
3. При решении системы уравнений межотраслевого баланса (МОБ) рекомендуется
a. Сформировать матрицу А из коэффициентов прямых затрат;
b. Сформировать единичную матрицу Е;
c. Найти матрицу Е-А;
d. Сформировать вектор-столбец свободных членов Y;
e. Применить один из методов решения СЛАУ (матричный, Крамера, команду Linsolve, методика использования которых изложена в [8, стр. 59-60, 67-70]) или
f. Найти матрицу, обратную матрице Е-А;
g. Умножить обратную матрицу (пункт f) на вектор-столбец Y.
h. Или предложить свой метод решения.
4. Распечатать протокол работы в Maple либо все введенные выражения и полученные в рабочем документе СКМ Maple результаты решений скопировать в буфер обмена, затем вставить в текстовый документ, в котором формируется контрольная работа.
ариант 1
· Изменение номинальной среднемесячной заработной платы описывается следующим полиномом:
 ,
,
где х - период.
Построить кривую изменения среднемесячной заработной платы за период с 1995 по 2010 год.
Вычислить предполагаемое значение заработной платы за 2000 и 2010 г.г.
· Решить систему уравнений межотраслевого баланса (МОБ)
По известным данным о коэффициентах прямых затрат (аij) и конечном продукте (Y) в межотраслевом балансе (МОБ) для трех отраслей (промышленность, строительство, сфера услуг) определить общий выпуск продукции по каждой отрасли (xij).
| Отрасль | Коэффициенты прямых затрат, aij | Конечный продукт Y, млрд.руб. | ||
| 0,1 | 0,3 | 0,4 | ||
| 0,2 | 0,2 | 0,5 | ||
| 0,2 | 0,2 | 0,1 |
· Построить поверхность
f = 2∙sin(xy), при x=-Pi..Pi, y=-Pi..Pi
· Вычислить значение производной первого порядка функции f(x):

· Ордината Y развертки верхней точки одной из деталей кроя швейного изделия определяется по формуле:
 , r=1.25
, r=1.25
Определить значение ординаты Y.
ариант 2
· Количество влаги W, необходимое для насыщения воздуха в прядильном зале предприятия, вычисляется по формуле
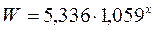 ,
,
где х - температура воздуха, оС.
Построить кривую изменения влажности в прядильном зале предприятия при температуре воздуха от 5 до 40оС.
Найти количество влаги, необходимое для насыщения воздуха при температуре 20оС 27оС.
· Решить систему уравнений межотраслевого баланса (МОБ)
По известным данным о коэффициентах прямых затрат (аij) и конечном продукте (Y) в межотраслевом балансе для трех отраслей (промышленность, строительство, сфера услуг) определить общий выпуск продукции по каждой отрасли (xij).
| Отрасль | Коэффициенты прямых затрат, aij | Конечный продукт Y, млрд.руб. | ||
| 0,2 | 0,2 | 0,1 | ||
| 0,5 | 0,3 | 0,2 | ||
| 0,2 | 0,1 | 0,4 |
· Построить поверхность
f = cos(x+y)-1 при x=-4..4, y=-4..4
· Вычислить значение производной первого порядка функции f(x):
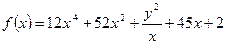
· Ордината Y развертки верхней точки одной из деталей кроя швейного изделия определяется по формуле:
 при r=1.85
при r=1.85
Определить значение ординаты Y.
ариант 3
· Интегральный уровень образования в Республике Беларусь описывается следующей зависимостью:
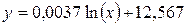 ,
,
где х – период.
Построить кривую изменения интегрального уровня образования в Республике Беларусь за период 2000-2015 г.г.
Вычислить предполагаемое значение интегрального уровня образования за 2008 и 2012 г.г. в Республике Беларусь
· Решить систему уравнений межотраслевого баланса (МОБ)
По известным данным о коэффициентах прямых затрат (аij) и конечном продукте (Y) в межотраслевом балансе для трех отраслей (промышленность, строительство, сфера услуг) определить общий выпуск продукции по каждой отрасли (xij).
| Отрасль | Коэффициенты прямых затрат, aij | Конечный продукт Y, млрд.руб. | ||
| 0,3 | 0,4 | 0,2 | ||
| 0,2 | 0,1 | 0,3 | ||
| 0,1 | 0,5 | 0,2 |
· Построить поверхность
f= Cos(tx) ∙sin(ty) при x=-Pi..Pi,y=-Pi..Pi, t=1..4
· Вычислить значение производной первого порядка функции f(x):
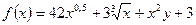
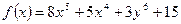
· Ордината Y развертки средней точки одной из деталей кроя швейного изделия определяется по формуле:
 при r=1.01
при r=1.01
Определить значение ординаты Y.
ариант 4
· Численность студентов на 10 тыс. человек населения описывается следующей зависимостью:
 ,
,
где х – период.
Построить кривую изменения численность студентов за 2000 – 2015 г.г. Определить предполагаемое значение численности студентов в 2009 и 2012 г.г.
· Решить систему уравнений межотраслевого баланса (МОБ)
По известным данным о коэффициентах прямых затрат (аij) и конечном продукте (Y) в межотраслевом балансе для трех отраслей (промышленность, строительство, сфера услуг) определить общий выпуск продукции по каждой отрасли (xij).
| Отрасль | Коэффициенты прямых затрат, aij | Конечный продукт Y, млрд.руб. | ||
| 0,2 | 0,4 | 0,4 | ||
| 0,1 | 0,5 | 0,2 | ||
| 0,1 | 0,2 | 0,1 |
· Построить поверхность
f = Sin(xy) приx=-Pi..Pi, y=-Pi..Pi
· Вычислить значение производной первого порядка функции f(x):
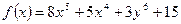
· Ордината Y развертки средней точки одной из деталей кроя швейного изделия определяется по формуле:

Определить значение ординаты Y.
ариант 5
· Объем производства чулочно-носочных изделий, млн. пар, предприятиями Республики Беларусь в зависимости от года выпуска можно описать полиномом пятой степени
 ,
,
где х – период.
Построить кривую изменения объема производства чулочно-носочных изделий, млн. пар, предприятиями Республики Беларусь за период с 1995 по 2005 г.г.
Определить предполагаемое количество пар чулочно-носочных изделий, выпущенных в 1998 и 2005 г.г.
· Решить систему уравнений межотраслевого баланса (МОБ)
По известным данным о коэффициентах прямых затрат (аij) и конечном продукте (Y) в межотраслевом балансе для трех отраслей (промышленность, строительство, сфера услуг) определить общий выпуск продукции по каждой отрасли (xij).
| Отрасль | Коэффициенты прямых затрат, aij | Конечный продукт Y, млрд.руб. | ||
| 0,1 | 0,4 | 0,5 | ||
| 0,1 | 0,5 | 0,4 | ||
| 0,2 | 0,2 | 0,1 |
· Построить поверхность
f=  при x = -10..10, y = =-Pi..Pi, t=1..4
при x = -10..10, y = =-Pi..Pi, t=1..4
· Вычислить значение производной первого порядка функции f(x):

· Ордината Y развертки средней точки одной из деталей кроя швейного изделия определяется по формуле:
 при r=1.1
при r=1.1
Определить значение ординаты Y.
ариант 6
· Индекс производства непродовольственных товаров в Республике Беларусь в зависимости от года выпуска можно описать полиномом пятой степени:
 ,
,
где х – период.
Построить кривую изменения индексов производства непродовольственных товаров в Республике Беларусь за период 1998 и 2005 год. Определить предполагаемые значения индексов производства непродовольственных товаров за 2000 и 2005 годы.
· Решить систему уравнений межотраслевого баланса (МОБ)
По известным данным о коэффициентах прямых затрат (аij) и конечном продукте (Y) в межотраслевом балансе для трех отраслей (промышленность, строительство, сфера услуг) определить общий выпуск продукции по каждой отрасли (xij).
| Отрасль | Коэффициенты прямых затрат, aij | Конечный продукт Y, млрд.руб. | ||
| 0,1 | 0,3 | 0,4 | ||
| 0,2 | 0,2 | 0,5 | ||
| 0,2 | 0,2 | 0,1 |
· Построить поверхность
f = Sin(x2+(y – 1)2) при x=-2..2, y=-1..3
· Вычислить значение производной первого порядка функции f(x):

· Ордината Y развертки средней точки одной из деталей кроя швейного изделия определяется по формуле:

Определить значение ординаты Y.
ариант 7
· Индекс общего объема продукции легкой промышленности в Республике Беларусь зависимости от года выпуска можно описать полиномом третьей степени:
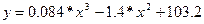
где х – год выпуска продукции.
Построить кривую изменения индексов общего объема продукции легкой промышленности в Республике Беларусь за период с 1995 по 2005 год. Определить предполагаемые значения индексов общего объема продукции легкой промышленности за 2001 и 2005 годы.
· Решить систему уравнений межотраслевого баланса (МОБ)
По известным данным о коэффициентах прямых затрат (аij) и конечном продукте (Y) в межотраслевом балансе для трех отраслей (промышленность, строительство, сфера услуг) определить общий выпуск продукции по каждой отрасли (xij).
| Отрасль | Коэффициенты прямых затрат, aij | Конечный продукт Y, млрд.руб. | ||
| 0,3 | 0,1 | 0,1 | ||
| 0,4 | 0,3 | 0,5 | ||
| 0,5 | 0,2 | 0,1 |
· Построить поверхность
f=(exy)xyпри x=-1..1,y=-1..1
· Вычислить значение производной первого порядка функции f(x):

· Ордината Y развертки нижней точки одной из деталей кроя швейного изделия определяется по формуле:
 при r=2.01
при r=2.01
Определить значение ординаты Y.
ариант 8
· Объем производства трикотажных изделий, млн. шт., предприятиями Республики Беларусь в зависимости от года выпуска можно описать следующей зависимостью:

де х – год выпуска продукции.
Построить кривую изменения объемов производства трикотажных изделий предприятиями Республики Беларусь за период с 1995 по 2005 год. Определить предполагаемые значения объемов производства трикотажных изделий за 1996 и 2005 годы.
· Решить систему уравнений межотраслевого баланса (МОБ)
По известным данным о коэффициентах прямых затрат (аij) и конечном продукте (Y) в межотраслевом балансе для трех отраслей (промышленность, строительство, сфера услуг) определить общий выпуск продукции по каждой отрасли (xij).
| Отрасль | Коэффициенты прямых затрат, aij | Конечный продукт Y, млрд.руб. | ||
| 0,2 | 0,3 | 0,3 | ||
| 0,1 | 0,1 | 0,1 | ||
| 0,4 | 0,5 | 0,4 |
· Построить поверхность
f = sin((x+2)t) при x=-10..10, t=1..20,n=1..50
· Вычислить значение производной первого порядка функции f(x):

· Ордината Y развертки нижней точки одной из деталей кроя швейного изделия определяется по формуле:
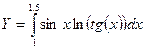
Определить значение ординаты Y.
ариант 9
· Объем выпуска ковровых изделий, млн. м2, предприятиями Республики Беларусь в зависимости от года выпуска можно описать следующей зависимостью:

где х – год выпуска продукции.
Построить кривую изменения объемов производства ковровых изделий предприятиями Республики Беларусь за период с 1995 по 2005 год. Определить предполагаемые значения объемов производства ковровых изделий за 2000 и 2005 годы.
· Решить систему уравнений межотраслевого баланса (МОБ)
По известным данным о коэффициентах прямых затрат (аij) и конечном продукте (Y) в межотраслевом балансе для трех отраслей (промышленность, строительство, сфера услуг) определить общий выпуск продукции по каждой отрасли (xij).
| Отрасль | Коэффициенты прямых затрат, aij | Конечный продукт Y, млрд.руб. | ||
| 0,1 | 0,5 | 0,4 | ||
| 0,2 | 0,2 | 0,1 | ||
| 0,2 | 0,4 | 0,4 |
· Построить поверхность
f=sin(x)×cos(x)×tan(x×y) при x=-4..4, y=-4..4
· Вычислить значение производной первого порядка функции f(x):
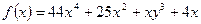
· Ордината Y развертки нижней точки одной из деталей кроя швейного изделия определяется по формуле:

Определить значение ординаты Y.
ариант 10
· Объем производства тканей, м2, предприятиями Республики Беларусь в зависимости от года выпуска можно описать следующей зависимостью:

где х – год выпуска продукции.
Построить кривую изменения объемов производства тканей, м2, предприятиями Республики Беларусь за период с 1998 по 2008 год. Определить предполагаемые значения объемов производства тканей, м2, за 2000 и 2008 годы.
· Решить систему уравнений межотраслевого баланса (МОБ)
По известным данным о коэффициентах прямых затрат (аij) и конечном продукте (Y) в межотраслевом балансе для трех отраслей (промышленность, строительство, сфера услуг) определить общий выпуск продукции по каждой отрасли (xij).
| Отрасль | Коэффициенты прямых затрат, aij | Конечный продукт Y, млрд.руб. | ||
| 0,2 | 0,2 | 0,1 | ||
| 0,5 | 0,3 | 0,2 | ||
| 0,2 | 0,4 | 0,3 |
· Построить поверхность
f =  при x=-4..4, y=-4..4
при x=-4..4, y=-4..4
· Вычислить значение производной первого порядка функции f(x):

· Ордината Y развертки нижней точки одной из деталей кроя швейного изделия определяется по формуле:
 при r=2.023
при r=2.023
Определить значение ординаты Y.






