еоретические основы построения математических моделей поверхностных акустических волн в упругих средах
сновные понятия
Для построения математических моделей поверхностных акустических волн в упругих средах необходимо ознакомится с основными понятиями в данной области.
Среда называется упругой, или линейной, если её деформация пропорциональна приложенной.
Упругими, или механическими волнами называются механические возмущения (деформации), распространяющиеся в упругих средах.
Звуковые или акустические волны — это волны, которые распространяются в упругой среде, характеризующиеся слабыми возмущениями. Это механические колебания с малыми амплитудами. Отсюда следует, что акустические волны являются упругими.
Наиболее распространёнными типами упругих волн в твёрдых телах являются:
· продольные волны — волны с колебанием частиц вдоль направления распространения волны;
· поперечные волны — волны с колебанием частиц перпендикулярно направлению распространения волны;
· поверхностные волны (например, волны Рэлея) — волны с колебанием частиц по эллипсам вдоль поверхности тела;
· волны Лэмба — волны в тонких пластинах;
· изгибные волны — распространение колебаний деформации изгиба в стержнях или пластинах, длина волны которых много больше толщины стержня или пластины.
При распространении акустической волны можно наблюдать следующие явления:
Резонанс – резкое возрастание амплитуды вынужденных колебаний при совпадении частоты изменения внешней силы, действующей на систему, с частотой свободных колебаний.
Интерференция – сложение в пространстве двух (или нескольких) волн, при котором образуется постоянное во времени распределение амплитуды результирующих колебаний в различных точках пространства.
Дифракция – отклонение от прямолинейного распространения волн, огибание волнами препятствий.
Угол отражения волны от поверхности равен углу падения (согласно принципу Гюйгенса).
Поверхностные акустические волны (ПАВ) — упругие волны, распространяющиеся вдоль поверхности твёрдого тела или вдоль границы с другими средами. ПАВ подразделяются на два типа: с вертикальной поляризацией и с горизонтальной поляризацией (волны Лява).
Возникновение и распространение акустических волн связано с упругими свойствами сред. Все реальные тела деформируемые. В случае твердых тел существует два предельных случая: деформации упругие и деформации пластические. Пределом упругости называют силу, до которой деформация будет упругой. Для идеально упругих тел между действующими сипами и деформациями существует однозначная связь, описываемая законом Гука: F=kDx.
Существует широкий класс твердых тел, для которых при малых деформациях этот закон приближенно справедлив. Существуют изотропные и анизотропные тела. Одно и то же тело может вести себя как изотропное по отношению к одним телам и воздействиям, и как анизотропное – по отношению к другим. По отношению к взаимодействиям, связанным с упругими свойствами все монокристаллические тела ведут себя как анизотропные.
астные случаи поверхностных акустических волн
К наиболее часто встречающимся частным случаям поверхностных волн можно отнести следующие:
1. Волны Рэлея (или рэлеевские), в классическом понимании распространяющиеся вдоль границы упругого полупространства с вакуумом или достаточно разреженной газовой средой. Энергия этих волн локализована в поверхностном слое толщиной от l до 2l, где l - длина волны. Частицы в волне Рэлея движутся по эллипсам, большая полуось w которых перпендикулярна границе, а малая u - параллельна направлению распространения волны (рис. 1).

Рис. 1 Поверхностная упругая волна Рэлея на свободной границе твердого тела
Обозначения:
х - направление распространения волны;
u,w - компоненты смещения частиц;
кривые изображают ход изменения амплитуды смещений при удалении от границы.
Фазовая скорость волн Рэлея c R» 0.9 c t, где c t - фазовая скорость плоской поперечной волны.
2. Затухающие волны рэлеевского типа на границе твердого тела с жидкостью, при условии, что фазовая скорость в жидкости с L < с R в твердом теле (что справедливо почти для всех реальных сред). Эта волна непрерывно излучает энергию в жидкость, образуя в ней отходящую от границы неоднородную волну (рис. 2).
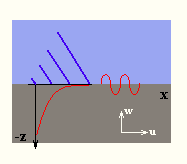
Рис. 2 Поверхностная упругая затухающая волна рэлеевского типа на границе твердого тела и жидкости
Обозначения:
х - направление распространения волны;
u,w - компоненты смещения частиц;
кривые изображают ход изменения амплитуды смещений при удалении от границы;
наклонные линии - фронты отходящей волны.
Фазовая скорость этой волны с точностью до процентов равна с R , коэффициент затухания на длине волны al ~ 0.1. Распределение по глубине смещений и напряжений - такое же, как в волне Рэлея.
3. Незатухающая волна с вертикальной поляризацией, бегущая по границе жидкости и твердого тела со скоростью, меньшей с L (и, соответственно, меньшей, чем скорости продольной и поперечной волн в твердом теле). Структура этой ПВ совсем другая, чем у рэлеевской волны. Она состоит из слабо неоднородной волны в жидкости, амплитуда которой медленно убывает при удалении от границы, и двух сильно неоднородных продольной и поперечной волн в твердом теле (рис. 3).

Рис. 3 Незатухающая ПВ на границе твердого тела и жидкости
Обозначения:
х - направление распространения волны;
u,w - компоненты смещения частиц;
кривые изображают ход изменения амплитуды смещений при удалении от границы.
Энергия волны и движение частиц локализованы в основном в жидкости.
4. Волна Стонли, распространяющаяся вдоль плоской границы двух твердых сред, модули упругости и плотности которых не сильно различаются. Такая волна состоит (рис. 4) как бы из двух рэлеевских волн - по одной в каждой среде.

Рис. 4 Поверхностная упругая волна Стонли на границе двух твердых сред
Обозначения:
х - направление распространения волны;
u,w - компоненты смещения частиц;
кривые изображают ход изменения амплитуды смещений при удалении от границы.
Вертикальные и горизонтальные компоненты смещений в каждой среде убывают при удалении от границы так, что энергия волны оказывается сосредоточенной в двух граничных слоях толщиной ~ l. Фазовая скорость волны Стонли меньше значений фазовых скоростей продольных и поперечных волн в обеих граничащих средах.
5.Волны Лява - ПВ с горизонтальной поляризацией, которые могут распространяться на границе твердого полупространства с твердым слоем (рис. 5).

Рис. 5 Поверхностная упругая волна Лява на границе "твердое полупространство - твердый слой"
Обозначения:
х - направление распространения волны;
кривые изображают ход изменения амплитуды смещений при удалении от границы.
Эти волны - чисто поперечные: в них имеется только одна компонента смещения v, а упругая деформация в волне Лява представляет собой чистый сдвиг. Смещения в слое (индекс 1) и в полупространстве (индекс 2) описываются выражениями:
v 1 = (A ¤ cos(s 1 h)) cos(s 1 (h - z))sin( w t - kx);
v 2 = A Чexp (s 2 z) sin( w t - kx), (1)
где t - время;
w - круговая частота;
s 1 = (k t12 - k 2)1/2;
s 2 = (k 2 - k t22)1/2;
k - волновое число волны Лява;
k t1, k t2 - волновые числа поперечных волн в слое и в полупространстве соответственно;
h - толщина слоя;
А - произвольная постоянная.
Из выражений для v 1 и v 2 видно, что смещения в слое распределены по косинусу, а в полупространстве экспоненциально убывают с глубиной. Для волн Лява характерна дисперсия скорости. При малых толщинах слоя фазовая скорость волны Лява стремится к фазовой скорости объемной поперечной волны в полупространстве. При w h ¤ c t2 >>1 волны Лява существуют в виде нескольких модификаций, каждая из которых соответствует нормальной волне определенного порядка.
К ПВ относят и волны на свободной поверхности жидкости или на границе раздела двух несмешивающихся жидкостей. Такие ПВ возникают под влиянием внешнего воздействия, например, ветра, выводящего поверхность жидкости из равновесного состояния. В этом случае, однако, упругие волны существовать не могут. В зависимости от природы возвращающих сил различают 3 типа ПВ: гравитационные, обусловленные в основном силой тяжести; капиллярные, обусловленные в основном силами поверхностного натяжения; гравитационно-капиллярные.






