обудова інтервального ряду наданої вибірки.
Весь проміжок  я розбив на 10 рівних за довжиною напіввідкритих інтервалів
я розбив на 10 рівних за довжиною напіввідкритих інтервалів  . Була підрахована кількість елементів вибірки, що потрапляють до кожного інтервала, відносні частоти та накопичені частоти. За представника кожного інтервлу
. Була підрахована кількість елементів вибірки, що потрапляють до кожного інтервала, відносні частоти та накопичені частоти. За представника кожного інтервлу  бралося значення з з вибірки що потрапило до цього інтервалу, найближче до середини інтервалу.
бралося значення з з вибірки що потрапило до цього інтервалу, найближче до середини інтервалу.
Величина інтервалів  .
.
Відповідні результати занесені до Таблиці 1.
Таблиця 1
| № |

|

|

|

| Середнє значення |

|
| [ 1,38; 1,478) | 0,07 | 0,07 | 1,429 | 1,43 | ||
| [ 1,478; 1,576) | 0,15 | 0,22 | 1,527 | 1,52 | ||
| [ 1,576; 1,674) | 0,08 | 0,3 | 1,625 | 1,64 | ||
| [ 1,674; 1,772) | 0,07 | 0,37 | 1,723 | 1,72 | ||
| [ 1,772; 1,87) | 0,05 | 0,42 | 1,821 | 1,83 | ||
| [1.87; 1.968) | 0,12 | 0,54 | 1,919 | 1,92 | ||
| [ 1,968; 2,066) | 0,13 | 0,67 | 2,017 | 2,02 | ||
| [ 2,066; 2,164) | 0,09 | 0,76 | 2,115 | 2,12 | ||
| [ 2,164; 2,262) | 0,15 | 0,91 | 2,213 | 2,21 | ||
| [ 2,262; 2,36 ] | 0,09 | 2,311 | 2,31 |
Точковий варіаційний ряд:

| 1.43 | 1.52 | 1.64 | 1.72 | 1.83 |
 1.92 1.92
| 2.02 | 2.12 | 2.21 | 2.31 |
| P | 0.07 | 0.15 | 0.08 | 0.07 | 0.05 | 0.12 | 0.13 | 0.09 | 0.15 | 0.09 |
Графічне зображення вибірки
Оскільки ми маємо інтервальний варіаційний ряд, то побудуємо гістограму відносних частот: на осі ОХ будуються напівінтервали з варіаційного ряду, по ОУ ставиться висота 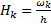 , де
, де  довжина відповідного інтервалу. Побудуємо таблицю з відповідними значеннями
довжина відповідного інтервалу. Побудуємо таблицю з відповідними значеннями  :
:
| № інтервалу | 
| Межі інтервалів | 
| 
|
| 1,429 | [ 1,38; 1,478) | 0,07 | 0.714 | |
| 1,527 | [ 1,478; 1,576) | 0,15 | 1.531 | |
| 1,625 | [ 1,576; 1,674) | 0,08 | 0.816 | |
| 1,723 | [ 1,674; 1,772) | 0,07 | 0.714 | |
| 1,821 | [ 1,772; 1,87) | 0,05 | 0.51 | |
| 1,919 | [1.87; 1.968) | 0,12 | 1.224 | |
| 2,017 | [ 1,968; 2,066) | 0,13 | 1.327 | |
| 2,115 | [ 2,066; 2,164) | 0,09 | 0.918 | |
| 2,213 | [ 2,164; 2,262) | 0,15 | 1.531 | |
| 2,311 | [ 2,262; 2,36 ] | 0,09 | 0.918 |

Емпірична функція розподілу
Емпіричною функцією розподілу називається функція розподілу дискретної випадкової величини, що набуває значення варіант  з ймовірністю
з ймовірністю  , тобто
, тобто
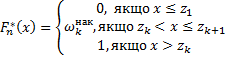
де 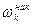 =
=  , тобто накопичена частість.
, тобто накопичена частість.
Побудуємо емпіричну функцію розподілу:

Функція намальована на окремому аркуші.
бчислити вибіркові медіану, моду, асиметрію.
Емпіричною (вибірковою) модою  називається варіанта
називається варіанта  , якій відповідає найбільша частість
, якій відповідає найбільша частість  .
.
Для заданого варіаційного ряду 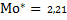
Емпіричною (вибірковою) медіаною 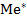 називають середню за розташуванням варіанту дискретного варіаційного ряду, якщо кількість варіант – непарна, і середнім арифметичним двох середніх за розташуванням варіант, якщо кількість варіант – парна.
називають середню за розташуванням варіанту дискретного варіаційного ряду, якщо кількість варіант – непарна, і середнім арифметичним двох середніх за розташуванням варіант, якщо кількість варіант – парна.
Для заданого варіаційного ряду Me* =  = 1,875
= 1,875
Емпіричним (вибірковим) коефіцієнтом асиметрії називають статистику  .
.
Вибіркове середнє обчислюється як  -1.43*0.07-1.52*0.15-1.64*0.08-1.72*0.07-1.83*0.05-1.92*0.12-2.02*0.13+2.12*0.76+2.21*0.15+2.31*0.09=1.8944
-1.43*0.07-1.52*0.15-1.64*0.08-1.72*0.07-1.83*0.05-1.92*0.12-2.02*0.13+2.12*0.76+2.21*0.15+2.31*0.09=1.8944 

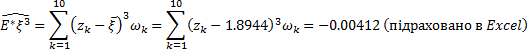

 = -0,17912
= -0,17912
найти незміщену оцінку математичного сподівання і дисперсії.
очкова оцінка параметра називають будь-яку функцію результатів спостережень над випадковою величиною (статистику), за допомогою якої судять про значення параметру:.
Точкова оцінка  параметра
параметра  називається незміщеною, якщо її математичне сподівання дорівнює оцінюваному параметру
називається незміщеною, якщо її математичне сподівання дорівнює оцінюваному параметру  , тобто
, тобто
 або
або  .
.
Знайдемо незміщену оцінку математичного сподівання:
 вибіркове середнє
вибіркове середнє

Незалежно від закону розподілу генеральної сукупності випадкової величини  оцінка
оцінка  буде завжди незміщеною для математичного сподівання. В 4 пункті вибіркове середнє вже було підраховано і дорівнює 1.8944– незміщена оцінка математичного сподівання.
буде завжди незміщеною для математичного сподівання. В 4 пункті вибіркове середнє вже було підраховано і дорівнює 1.8944– незміщена оцінка математичного сподівання.
Тепер перейдемо до знаходження незміщеної оцінки дисперсії:
 . Це буде дорівнювати:
. Це буде дорівнювати:
 .
.
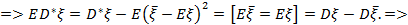 оцінка зміщена.
оцінка зміщена.
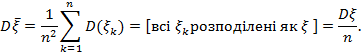
=> 
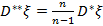 – виправлена вибіркова дисперсія, вводиться для ліквідації зсуву.
– виправлена вибіркова дисперсія, вводиться для ліквідації зсуву.

Звідси виправлена випадкова дисперсія є незміщеною оцінкою генеральної сукупності. Підрахуємо її для конкретної реалізації вибірки:

Висунути гіпотезу про розподіл, за яким отримано вибірку
Асиметрія близька до нуля, кумулятивна крива майже нагадує пряму, вибіркове середнє  (1.8944 та 1.875 відповідно) – це дає право висунути гіпотезу про розподіл генеральної сукупності:
(1.8944 та 1.875 відповідно) – це дає право висунути гіпотезу про розподіл генеральної сукупності:  , та гіпотезу
, та гіпотезу  .
.
Перевірити за допомогою критерію  (Пірсона) гіпотезу про розподіл з рівнем значущості
(Пірсона) гіпотезу про розподіл з рівнем значущості  = 0,05.
= 0,05.
Для того, щоб можна було скористатись критерієм Персона, нам прийдеться перерозбити числову вісь на інтервали, що приведені в таблиці. Для таких інтервалів:

Де  - ймовірність потрапляння рівномірної генеральної сукупності з щільність розподілу
- ймовірність потрапляння рівномірної генеральної сукупності з щільність розподілу 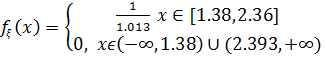 у інтервал
у інтервал  .
.
Це дуже легко перевірити.
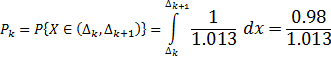
 - кількость значень елементів вибірки, які потрапили в інтервал
- кількость значень елементів вибірки, які потрапили в інтервал  . r=10;
. r=10;
Кількість невідомих параметрів, замінених на їх оцінки s = 2.
З таблиць знаходимо: 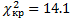 .
.

| 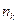
| 
| 
| 
| 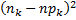
| 
|
( ,1.477) ,1.477)
| 0,1 | -3 | 0,9 | |||
| [1.477;1.575) | 0,1 | 2,5 | ||||
| [1.575;1.673) | 0,1 | -2 | 0,4 | |||
| [1.673; 1.771) | 0,1 | -3 | 0,9 | |||
| [1.771; 1.869) | 0,1 | -5 | 2,5 | |||
| [1.869; 1.967) | 0,1 | 0,4 | ||||
| [1.967; 2.065) | 0,1 | 0,9 | ||||
| [2.065; 2.163) | 0,1 | -1 | 0,1 | |||
| [2.163;2.263) | 0,1 | 2,5 | ||||
[2.262;  ) )
| 0,1 | -1 | 0,1 |
За означенням, рівень значущості  , це ймовірність помилки 1-го роду.Помилка 1-го роду в нашій задачі буде тоді, коли
, це ймовірність помилки 1-го роду.Помилка 1-го роду в нашій задачі буде тоді, коли  буде перевищувати деяке «порогове» значення тобто
буде перевищувати деяке «порогове» значення тобто  .
.
Для нашої вибірки 
Отже, висунута гіпотеза правильна з рівнем значущості 






