1. На плоскости даны два вектора  и
и 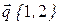 . Найти разложение вектора
. Найти разложение вектора  по базису
по базису  и
и 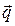 .
.
2. Даны три вектора 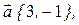
 и
и  . Найти разложение вектора
. Найти разложение вектора 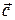 по базису
по базису 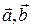 .
.
3. Даны три вектора 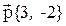 ,
, 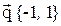 . Найти разложение вектора
. Найти разложение вектора 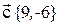 по базису
по базису 
4. Даны четыре вектора: 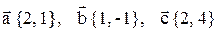 . Найти разложение вектора
. Найти разложение вектора 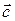 по векторам
по векторам 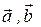 .
.
5. Векторы  и
и  образуют угол
образуют угол 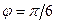 ; зная, что
; зная, что  , найти скалярное произведение векторов
, найти скалярное произведение векторов  и
и 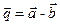 .
.
6. Найти скалярное произведение векторов 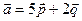 и
и 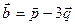 , если
, если  и
и 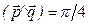 .
.
7. Известно, что | 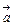 |=3, |
|=3, |  |= 4;
|= 4;  . Вычислить: скалярное произведение векторов
. Вычислить: скалярное произведение векторов 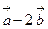 и
и 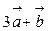 .
.
8. Векторы  и
и 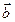 образуют угол
образуют угол  ; зная, что
; зная, что  , найти скалярное произведение векторов
, найти скалярное произведение векторов  и
и 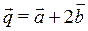 .
.
9. Даны вершины треугольника А (2, –5), В (1, –2), С (4, 7). Вычислить координаты центра тяжести этого треугольника. Найти длину медианы АМ.
10. Даны вершины треугольника А (–1, –1), В (3, 5), С (–4, 1). Вычислить координаты центра тяжести этого треугольника. Найти длину медианы ВМ.
11. Даны вершины треугольника А (1, 4), В (3, –9), С (–5, 2). Вычислить координаты центра тяжести этого треугольника. Найти длину медианы АМ.
12. Даны вершины треугольника А (3, –1), В (1, 1), С (2, 3). Вычислить координаты центра тяжести этого треугольника. Найти длину медианы ВМ.
13. Точка 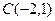 делит отрезок АВ в отношении
делит отрезок АВ в отношении 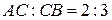 . Найти координаты точки В, если
. Найти координаты точки В, если  .
.
14. Точка  делит отрезок АВ в отношении
делит отрезок АВ в отношении  . Найти координаты точки А, если
. Найти координаты точки А, если 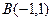 .
.
15. Отрезок АВ двумя точками разделен на три равные части. Определить координаты точек деления, если 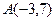 ,
,  .
.
16. Точка 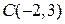 делит отрезок АВ в отношении
делит отрезок АВ в отношении  . Найти координаты точки В, если
. Найти координаты точки В, если  .
.
17. Составить уравнение эллипса, фокусы которого лежат на оси абсцисс симметрично относительно начала координат, если его малая ось равна 6, а расстояние между директрисами равно 13.
18. Составить уравнение эллипса, фокусы которого лежат на оси ординат симметрично относительно начала координат, если расстояние между фокусами 24, а эксцентриситет равен 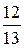 .
.
19. Составить уравнение гиперболы, фокусы которой расположены на оси абсцисс симметрично относительно начала координат, если она имеет асимптоты 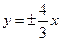 и расстояние между фокусами равно 20.
и расстояние между фокусами равно 20.
20. Составить уравнение гиперболы, фокусы которой расположены на оси абсцисс симметрично относительно начала координат, если расстояние между директрисами равно 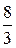 и эксцентриситет равен
и эксцентриситет равен 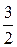 .
.
21. Составить уравнение параболы, вершина которой находится в начале координат, парабола симметрична относительно оси Ох и проходит через точку А (1, 3).
22. Составить уравнение параболы, вершина которой находится в начале координат, парабола симметрична относительно оси Ох и проходит через точку А (–4, 2).
23. Составить уравнение параболы, вершина которой находится в начале координат, парабола симметрична относительно оси Оу и проходит через точку А (3, –5).
24. Составить уравнение параболы, вершина которой находится в начале координат, парабола симметрична относительно оси Оу и проходит через точку А (–2, 1).
25. Даны вершины треугольника АВС А (1;1;-2), В (1;1;0), С (-1;3;0). Вычислить длину его высоты АН. (Используя векторное произведение векторов)
26. Дан треугольник АВС, в котором А (-1;1;2), В (1;1;0), С (2;6;-2). Вычислить длину его высоты ВН. (Используя векторное произведение векторов)
27. Дан треугольник АВС, в котором А (-1;1;2), В (1;1;0), С (2;6;-2). Вычислить площадь треугольника АВС, длину высоты CH. (Используя векторное произведение векторов)
28. Дан треугольник АВС, в котором А (6;5;-1), В (12;1;0), С (1;4;-5). Вычислить площадь треугольника АВС, длину высоты CH. (Используя векторное произведение векторов)
29. Вычислить объем тетраэдра, вершины которого находятся в точках
А (2;-1;0), В (5;4;3), С (3;1;-1) и D (4;-1;3).
30. Даны вершины тетраэдра: А (-2;3;0), В (4;2;-1), С (5;3;6), D (-4;-5;9). Найти длину его высоты, опущенной из вершины Д.
31. Объём тетраэдра V=7, три его вершины находятся в точках А(-2;0;-1), В(3;-1;1), С(2;-1;4). Найти координаты четвертой вершины Д, если известно, что она лежит на оси Oу.
32. Даны вершины тетраэдра: А(7;5;-1), В(0;-2;1), С(2;-2;4), Д(-4;1;3). Найти длину его высоты, опущенной из вершины В.
33. Составить уравнение плоскости, которая проходит через точку с координатами М1(3;-2;-7) и параллельно плоскости 2x-3z+5=0.
34. Составить уравнение плоскости, которая проходит через начало координат перпендикулярно к двум плоскостям: 2x-y+3z-1=0, x+2y+z=0.
35. Составить уравнение плоскости, которая проходит через точку М1(2;-1;1) перпендикулярно к двум плоскостям: 2x-z+1=0, y=0.
36. Составить уравнение плоскости, которая проходит через две точки
М1(1;-1;-2) и М2(3;1;1) перпендикулярно к плоскости x-2y+3z-5=0.
37. Составить уравнения прямой, которая проходит через точку М1(-1;2;-3) параллельно прямой: 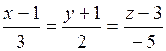 .
.
38. Составить уравнения прямой, которая проходит через точку М1(-4;-5;3) параллельно прямой: 
39. Составить уравнение прямой, которая проходит через точку М1(2;3;-5) параллельно прямой: x=3t-7, y=-2t+4, z=3t+4.
Составить каноническое уравнения прямой, которая проходит через точку М0(3;-2;-4) параллельно прямой 
40. Вычислить кратчайшее расстояние между двумя прямыми в каждом из следующих случаев:
1) 

2) x=2t-4, y=-t+4, z=-2t-1;
x=4t-5, y=-3t+5, z=-5t+5
3) 

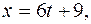 y=-2t, z=-t+2
y=-2t, z=-t+2
4) 

41. Даны вершины эллипсоида А 1(8;0;0); А 2(-2;0;0). Написать уравнение этого
эллипсоида, зная, что плоскость YOZ пересекает его по эллипсу: x =0, 
42. Оси симметрии однополостного гиперболоида Ф служат осями
ортонормированного репера и Ф проходит через эллипс 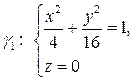 и
и
гиперболу 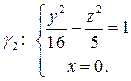 Написать уравнение гиперболоида Ф.
Написать уравнение гиперболоида Ф.
43. Оси симметрии однополостного гиперболоида служат осями ортонормированного репера. Написать уравнение этого гиперболоида, если он проходит через линию 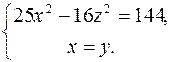 и точку М0(3;4;3).
и точку М0(3;4;3).
44. Написать уравнение эллипсоида, оси которого совпадают с осями координат и который проходит через точку М0(3;1;0) и пересекает плоскость хОz по эллипсу 






