x(t) — нормированный белый шум.

етерминированные сигналы.

лучайные сигналы.

Цель: научиться проводить моделирование и обробітку сигналов.

 

Задание:

1. Провести моделирование сигналов S₁(t), S₂(t), S₃(t), параметры сигналов указаны в таблице

S₁(t)=A₁*sin(2pf₁t);

S₂(t)=A₂*sin(2pf₂t)+ S₁(t);

S₃(t)=S₂+x(t);

x(t) — нормированный белый шум.

	№	А1	А2	f1	f2
	0.8	0.7

1. Построить график всех сигналов, которые промодулированы. Моделирование нормально белого шума проводить с помощью функции random().

Найти для всех сигналов (S₁(t), S₂(t), S₃(t)) среднее, дисперсию, энергию, мощность. Построить гистограмму белого шума.

 

 

 

 

4.Выводы:

 

Сигналы могут быть одномерными или многомерными, зависит это от количества переменных.

Классификация сигналов основана на возможности или невозможности точного предсказания значения сигнала в любой момент времени или в любой точке пространственных координат.

В первом случае сигналы называются детерминированными, а во втором – случайными.

Случайные сигналы описываются случайными функциями. Случайную функцию времени называют случайным процессом.

 

 

1. По видам (типам) сигналов выделяются следующие:

1. Аналоговый - является непрерывной функцией непрерывного аргумента, т.е. определен для любого значения аргументов.

1. Цифровой – являются искусственным, т.е. их можно получить только путем преобразования аналогового электрического сигнала.
2. Дискретный - по своим значениям также является непрерывной функцией, но определенной только по дискретным значениям аргумента.

2. Непрерывные аналоговые сигналы имеют три основные характеристики:

• амплитуду;

• длину волны;

• частоту.

3. Характеристики:

1. Длительность сигнала Т _с – интервал времени, на протяжении которого существует сигнал.
2. Ширина спектра F _c – диапазон частот, в пределах которых сосредоточена основная мощность сигнала.
3. База сигналу - умножение ширины спектру сигнала на его длительность.
4. Динамичный диапазон D _c - логарифм отношения максимальной мощности сигнала - P _max к минимальной - P _min
5. Объем сигнала выражается отношением V _c = T _c F _c D _c.
6. Энергетические характеристики: моментальная мощность - P (t); средняя мощность - P _СР і энергия - E. Эти характеристики выражается отношением:
P (t) = x ² (t); ; 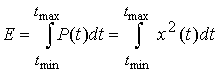(1)
де T = t _max - t _min.

4. Белый шум — стационарный шум, спектральные составляющие которого равномерно распределены по всему диапазону задействованных частот. Примерами белого шума являются шум близкого водопада (отдаленный шум водопада — розовый, так как высокочастотные составляющие звука затухают в воздухе сильнее низкочастотных), или дробовой шум на клеммах большого сопротивления, или шум стабилитрона, через который протекает очень малый ток.

5. Когерентные и ортогональные сигналы.

В физике когерентностью называется скоррелированность (согласованность) нескольких колебательных или волновых процессов во времени, проявляющаяся при их сложении. Колебания когерентны, если разность их фаз постоянна во времени, и при сложении колебаний получается колебание той же частоты.

Классический пример двух когерентных колебаний — это два синусоидальных колебания одинаковой частоты.

Когерентные - сигналы, совпадающие во всех точках определения.

Ортогональные - сигналы противоположные когерентным.

6. Норма — функционал, заданный на векторном пространстве и обобщающий понятие длины вектора или абсолютного значения числа.

Ортогональный базис — базис, составленный из попарно ортогональных векторов.

Ортонормированный базис удовлетворяет еще и условию единичности нормы всех его элементов. То есть это ортогональный базис с нормированными элементами.

7. Функция - производная функции распределения – характеризует плотность, с которой распределяются значения случайной величины в данной точке. Эта функция называется плотностью распределения (иначе – «плотность вероятности») непрерывной случайной величины.

8. Стационарный процесс – все вероятностные характеристики, не меняющиеся с течением обстоятельств.