рямые методы построения регрессионных моделей.

 

При предположениях о линейной регрессионной зависимости и нормальном законе условного распределения эмпирическое уравнение регрессии можно написать без использования какого-либо критерия близости точек к кривой .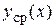

В корреляционноманализе вычисляют сначала средние арифметические, несмещенные оценки средних квадратических отклонений и коэффициентов корреляции: 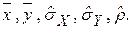Тогда эмпирическое уравнение регрессии записывается следующим образом: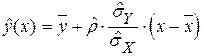

Оно имеет тот же вид, что и само уравнение регрессии для двумерного нормального распределения. Поскольку X и Y – обе случайные величины, то можно записать еще одно эмпирическое уравнение регрессии:

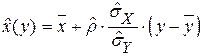
В регрессионном анализе может быть использован тот же метод, только вычисляемые значения нельзя трактовать как оценки параметров распределения. Но лучше записывать эмпирическое уравнение регрессии в виде:

,

где

Доверительный интервал для условного математического ожидания имеет вид, приведенный при изложении метода наименьших квадратов. Оценку среднего квадратического отклонения условного распределения можно вычислять по более простой формуле:

 

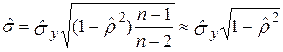
4.3. Использование регрессионных моделей

 

Пусть получена модель 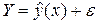, причем найдены оценки: , ,

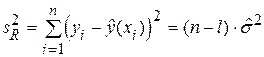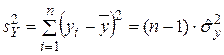где 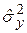имеет смысл оценки дисперсии только в корреляционном анализе, т.е. когда проводится пассивный эксперимент.

Прежде всего, оценивается величина, называемая выборочным коэффициентом детерминации, а часто просто коэффициентом детерминации и характеризующая степень тесноты детерминированной связи:

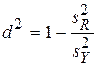
Чем ближе к единице этот коэффициент, тем ближе статистическая зависимость между y и x к функциональной (детерминированной), если, конечно, в качестве функции 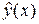не взят, вопреки здравому смыслу, полином n –ой степени, проходящий через все точки .

Находится оценка корреляционного отношения:

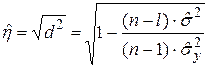
В случае линейной регрессии и при нормальном законе выполняется равенство: 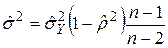. Если эту формулу подставить в предыдущую, в которой принять l= 2, то получим: 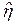= 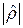. Если при предположении нелинейной регрессии величина 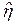оказалась близкой к 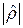, значит, в качестве 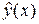можно брать линейную функцию. Нетрудно убедиться, что всегда .

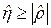Регрессионная модель используется для косвенного оценивания значения 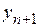по вновь полученной информации только о значении 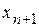, если, конечно, можно считать неизменными условия наблюдений. Подставляя 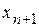в выражение для 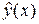, мы оценим только среднее значение величины y с некоторым доверительным интервалом (для линейной регрессии он приведен выше). При больших значениях n величиной доверительного интервала можно пренебречь. Тогда оценку индивидуального значения 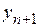мы можем написать в виде интервала, в который с заданной вероятностью p попадет это значение:

,

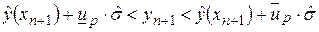где 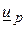и 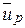– нижний и верхний квантили распределения случайной величины 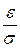(в случае нормального распределения 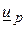= – 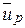). При малых n или значениях 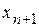, далеко отстоящих от 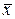, надо пользоваться толерантным интервалом, который получается путем расширения приведенного выше интервала с каждой стороны на половину длины доверительного интервала.

В частности, для нормального условного распределения и при 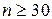можно приблизительно с вероятностью p = 0,95 утверждать, что 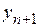будет находиться в интервале

.

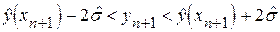В случае, когда параметр 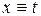– время (в частном случае, когда t=1,2,3,…, регрессионная модель называется трендовой), косвенное оценивание обычно представляет собой прогнозирование. Однако регрессионные модели для прогнозирования надо использовать очень осторожно.

Во-первых, прогноз можно осуществлять, как правило, лишь на небольшую глубину в стабильной обстановке, т.е. при предположении о неизменности основных условий протекания процессов.

Во-вторых, регрессионная модель в случаях, когда 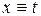, не учитывает инерционность системы, она допускает возможность резких изменений величины y через малое время .

Эти же замечания можно сделать и по отношению к пространственному параметру x, представляющему собой, например, расстояние.

В таких случаях лучше использовать (желательно в сочетании с экспертными методами) модели случайных процессов, учитывающих автокорреляцию: марковских, полумарковских, процессов с независимыми приращениями, т.е. 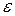должна быть не случайной величиной, а случайным процессом.

Прогнозирование на основе регрессионных моделей можно осуществлять и когда x не является параметром времени, но значения 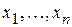по сравнению с 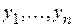сдвинуты во времени, т.е. имеют временной лаг, который можно принять за глубину прогноза.

Косвенное оценивание по регрессионным моделям часто позволяет значительно сэкономить ресурсы.

Кроме косвенного оценивания регрессионные модели могут служить эталоном нормально протекающих процессов в природе или человеческой деятельности. Например, между средней зарплатой и количеством автомобилей в регионе (в частности, районе области) имеется определенная статистическая зависимость. Однако некоторые регионы могут иметь низкую среднюю заработную плату и в то же время большое число автомобилей на душу населения. Это наводит на мысль о наличии очень развитой теневой экономики в регионе.

Задача. На предприятии ведется учет числа рекламаций, получаемых от потребителей. Пусть детали типа A отправляются одному потребителю, а детали типа B – другому. Ежемесячное число рекламаций x и y по деталям типа A и B соответственно представлено в таблице:

Месяцы

x

y

 

Провести корреляционный анализ на наличие временного лага l 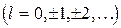между значениями параметров, построить регрессионную модель и предложить метод прогноза числа рекламаций.

При l = 0 для статистической обработки надо брать пары: (105;68); (102;71) и т.д.

При l = 1 – пары (105;71); (102;69) и т.д. (этих пар будет только 11).

При l = –1 – пары (102;68); (100;71) и т.д.

Пусть сначала l = 0. Находим:

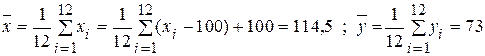
Вычислим несмещенные оценки дисперсий. Это легче сделать по следующим формулам:

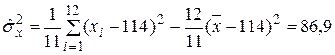
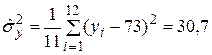
Находим оценки средних квадратических отклонений:

Определим несмещенную оценку ковариации:

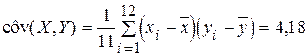
Наконец, вычисляем оценку коэффициента корреляции:

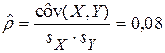
Отсюда следует, что при l = 0 величины X и Y практически некоррелированы.

Пусть теперь l = 2. Находим

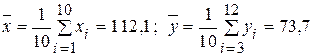
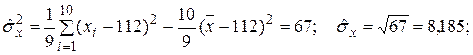
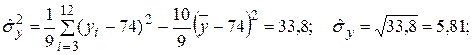
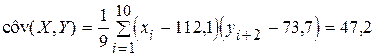
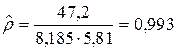
Оценка коэффициента корреляции при l = 2 оказалась близкой к 1, что означает наличие почти детерминированной зависимости между x и y. В этом можно убедиться, если точки 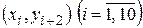нанести на координатную плоскость (x, y).

Можно также самостоятельно убедиться в том, что при других l оценки коэффициента корреляции будут меньше 0,993. Значит, в статистических данных исходной таблицы имеется лаг l =2. Это означает, что, получив число рекламаций, поступивших, например, за январь по деталям типа A, можно довольно точно спрогнозировать число рекламаций по деталям типа B, которое будет в марте. Прогнозирование надо осуществлять на основе уравнения регрессии:

В частности, при x = 125 получим 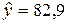. Это число мало отличается от числа y = 82 (см. таблицу). Но это – прогноз в среднем.

Точность индивидуального прогноза определяется, во-первых, естественным разбросом, т.е. дисперсией условного распределения 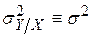, а во-вторых, ограниченностью выборки, т.е. доверительным интервалом для величины 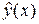, который зависит от x.

Определим оценку среднего квадратического отклонения условного распределения по более простой формуле: 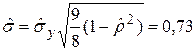. С целью определения доверительного интервала для условного математического ожидания при 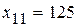зададимся значением 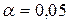. Из табл. 3П Приложения находим квантиль 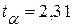распределения Стьюдента с (n – 2) степенями свободы, т.е. при k = 8. Тогда, учитывая, что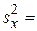 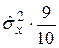, находим:

.

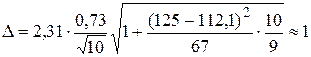Доверительный интервал имеет вид: ,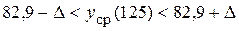

т.е.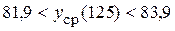

Зададим вероятность p = 0,95 попадания индивидуального значения 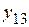в искомый интервал при предположении, что математическое ожидание 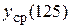известно точно. Из табл. 1П Приложения найдем квантиль 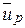=1,96. Тогда этот интервал имеет вид:

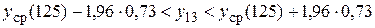
или: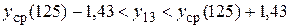

Объединяя полученные два интервала, запишем интервал для индивидуального прогноза величины :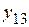

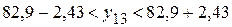или: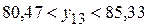

Этот интервал зависит от двух вероятностей: 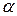и p.

 

5. Проверка статистических гипотез

 

5.1. Основные понятия

 

Определение. Статистическая гипотеза (или просто – гипотеза) – это некоторое предположение относительно характеристик генеральной(-ых) совокупности(-ей), выдвигаемое на основе выборки(-ок).

Гипотез может быть несколько (например, в задачах классификации, распознавания образов), но обычно их число равно двум. При этом выделяют основную гипотезу, соответствующую наиболее вероятному состоянию некоторой системы или наиболее вероятному виду объекта, подлежащего распознаванию. Ее обозначают H₀. Наряду с основной гипотезой часто рассматривают альтернативную – Н₁. Например, в технологической системе, производящей продукцию, обычно выделяют исправное и неисправное состояния. Числовые характеристики (математическое ожидание, дисперсия или вероятность попадания случайных величин в заданную область, т.е. процент годных единиц продукции) генеральных совокупностей, соответствующих продукции, выпущенной исправной и неисправной технологической системой, имеют разные значения. Распознать состояние технологической системы можно на основе информации о выборке из генеральной совокупности, если заранее провести необходимые исследования.

Задачи проверки гипотез относят к задачам статистического анализа. Различают параметрические и непараметрические гипотезы, простые и сложные.

Непараметрическая гипотеза – гипотеза о характере распределения (-ий). Различают три вида гипотез: 1) гипотеза о виде распределения, выдвигаемая на основе одной выборки (например, распределение является нормальным); 2) гипотеза о равенстве (об одинаковости) распределений, выдвигаемая на основе выборок, извлекаемых из разных генеральных совокупностей или слоев; 3) гипотеза об одинаковости видов распределений, выдвигаемая на основе выборок, извлекаемых из разных генеральных совокупностей или слоев.

Параметрическая гипотеза – гипотеза о значениях параметров распределения(-ий) известного вида или числовых характеристик случайной величины.

Параметр распределения или числовую характеристику случайной величины будем обозначать h. Это может быть и вектор. Проверка параметрических гипотез применяется для двух типов задач: сравнение оценки числовой характеристики (математического ожидания, вероятности успеха и пр.) с конкретным числом либо сравнение между собой оценок, полученных по нескольким выборкам, взятым из разных генеральных совокупностей или различных слоев.

Задачи I типа применяются для обоснования принятия решений при выборочном контроле качества продукции, распознавании образов, обработке результатов тестирования, контроле состояния или умонастроений различных слоев общества, контроле окружающей среды, контроле истинного экономического состояния предприятий, и т.д.

Задачи II типа применяются с целью решения вопроса о возможном объединении генеральных совокупностей в одну, для оценки возможности применения к разным генеральным совокупностям одной и той же методики выборочного контроля, для сравнительной оценки эффективности различных способов деятельности и т.д. Эти задачи составляют основу дисперсионного анализа.

Проверка параметрических гипотез для задач I типа осуществляется с применением различных критериев оптимальности принимаемых решений: Неймана-Пирсона, Байеса, Вальда (минимаксного или максиминного критерия), Гурвица и др. Задачи I типа часто успешнее решаются в рамках теории исследования операций методами теории статистических решений (ее называют также статистическими играми или играми с природой), более общей по сравнению с теорией проверки гипотез.

Простая гипотеза – параметрическая гипотеза о значении параметра (одномерного или многомерного). Обычно пишут: Н₀: h= h₀, Н₁: h = h₁.

Сложная гипотеза – параметрическая гипотеза о совокупности значений параметра. Гипотезы Н₁: h ¹ h₀ и Н₁: h < h_0, являются сложными. Сложной может быть и Н₀. Области S₀ и S₁ значений параметра h, соответствующие сложным гипотезам Н₀ и Н₁, могут не пересекаться, а могут иметь и общие элементы.

Правило, по которому принимают или отвергают гипотезу H₀, называют критерием. Правило зависит от вида альтернативной гипотезы. Оно определяет границу в пространстве выборки x =(x₁, x₂, …, x_n), где n – объем выборки, или в пространстве так называемых тестовых статистик t, являющихся функциями от x₁, …, x_n. Тестовыми статистиками обычно являются точечные оценки числовых характеристик и функции от них. Граница отделяет области принятия R (или G) и отклонения 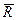(или 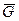) гипотезы H₀, где R соответствует пространству выборки, а G – пространству тестовых статистик. Принятие или отклонение гипотезы H₀ влечет за собой принятие некоторого решения в процессе управления, основанного на выборочных исследованиях (в том числе – неточных измерениях). Критерием часто называют саму тестовую статистику.

Ввиду случайности выборки возможны ошибки в принятии или отклонении гипотезы H₀: ошибкой I рода называют отклонение гипотезы H₀ в то время, когда она верна, ошибкой II рода называют принятие гипотезы H₀ в то время, когда верна альтернативная гипотеза H₁. Значит, можно говорить и о вероятностях ошибок I и II рода. Как правило, ими называют условные вероятности ошибок, предполагая, что H₀ и H₁ – простые гипотезы.

Вероятностью ошибки первого рода называют условную вероятность отклонения гипотезы H₀ (при условии, что она верна):

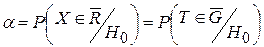
Вероятностью ошибки второго рода называют условную вероятность принятия гипотезы H₀ (при условии, что верна альтернативная гипотеза H₁):

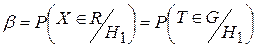
Вероятности a и b называют также условными рисками или просто рисками. Их выбирают обычно из ряда: 0,1; 0,05; 0,01; 0,005; 0,001. Вероятность a называют еще и уровнем значимости, а вероятность 1-b – мощностью критерия.

Если отклонение гипотезы H₀ означает автоматическое принятие гипотезы H₁, то a – условная вероятность принятия гипотезы H₁. Но в результате отклонения гипотезы H₀ могут приниматься и другие решения. Чаще всего – это получение дополнительной информации: берется еще одна выборка, уточняются предположения относительно вида закона распределения и пр.

Если известны априорные вероятности p и q гипотез H₀ и H₁ соответственно, то вводят в рассмотрение безусловные вероятности ошибок I и II рода (безусловные риски): a_б=р∙a, b_б=q∙b. Это – вероятности произведения событий.

В случае сложных гипотез H₀ (если h 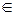S₀) и H₁ (если h 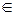S₁) условные риски a и b зависят от значения параметра h. Тогда вместо них рассматривают полные условные вероятности ошибок:

a_п.y= , b_п.y= ,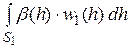

где w₀(h) и w₁ (h) – плотности вероятностей параметра h, при условии, что справедлива гипотеза H₀ или H₁ соответственно.

В распространенном частном случае, когда альтернативная сложная гипотеза H₁ есть логическое отрицание основной сложной гипотезы H₀ и известны априорные вероятности p и q=1-p гипотез H₀ и H₁ соответственно, априорное распределение параметра h, согласно модифицированной формуле полной вероятности, можно представить в виде:

w(h)=pw₀(h)+ qw₁(h)

В этом случае часто бывает легче оценить сначала w(h). Тогда

p= 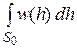, q = ,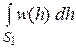

w₀(h)= 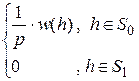, w₁(h)=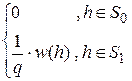

Рассматривают также полные безусловные вероятности ошибок:

a_п.б=pa_п.y = 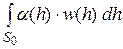, b_п.б = qb_п.y =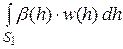

В зависимости от задачи может использоваться только одна вероятность ошибки I рода или обе. В случае, когда гипотеза H₀ – простая, а альтернативная гипотеза H₁ – сложная, обычно используют только один условный риск a.

При практическом применении теории проверки гипотез в задачах принятия решений в условиях неопределенности часто возникают трудности с определением границ между сложными гипотезами H₀ и H₁. Например, какие партии продукции, подлежащие выборочному контролю, считать приемлемыми, а какие неприемлемыми или какие предприятия, подлежащие выборочному инспектированию, считать злостными нарушителями законов? Такие задачи можно решать методами теории статистических решений, которая в таких случаях может обходиться без термина “гипотеза”. Для их решения используется также сравнительно недавно созданный аппарат теории расплывчатых множеств, однако при правильном его применении результаты решения задач совпадают с результатами, получаемыми на основе использования теории вероятностей и математической статистики.

 

5.2. Проверка непараметрических гипотез

 

Проверка основана на использовании только основной гипотезы H₀ (альтернативная совпадает с ее логическим отрицанием). В этом случае имеет смысл вводить в рассмотрение только одну вероятность ошибки первого рода a.

Рассмотрим только первый вид непараметрической гипотезы из трех, упомянутых выше. Иначе говоря, рассмотрим только задачи одного типа. Это задачи подбора теоретического распределения (экспоненциального, нормального и т.д.) на основе выборки из генеральной совокупности. Применяются, например, при периодическом контроле процесса изготовления партий продукции, методика контроля качества которых основана на предположении о нормальном распределении параметра изделия внутри партии.

Проверка непараметрических гипотез для этих задач осуществляется на основе некоторого критерия согласия, который основан на использовании меры расхождения между теоретическим распределением и результатами обработки информации о выборке. Обычно используют критерии Пирсона, Колмогорова. Здесь рассмотрим только один – критерий Пирсона. Он наиболее распространен.

 

Критерий согласия Пирсона (критерий c²) относительно закона распределения

Основан на использовании тестовой статистики t≡u, являющейся мерой расхождения между теоретическим и эмпирическим распределениями:

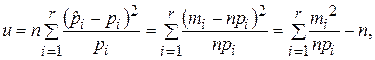
где r – количество интервалов разбиения области значений параметра x при построении гистограммы или эмпирической функции распределения;

m_i (i=1, …, r) – количество значений параметра x ввыборке, оказавшихся в i- оминтервале [b_i-1, b_i);

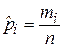– эмпирические вероятности попадания X в интервал [b_i-1, b_i):

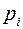– вероятности попадания случайной величины X в интервал [b_i-1, b_i):

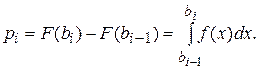
Закон распределения случайной величины U при увеличении n приближается к распределению c² с (r-l-1) степенями свободы, где l– число неизвестных параметров распределения.

Из двух гипотетических теоретических распределений лучше согласуется с выборочными данными то, при котором величина u окажется меньше.

На практике процедуру подбора теоретического распределения осуществляют следующим образом. Исходя из построенной гистограммы, делают предположение о виде закона распределения, в качестве значений параметров которого принимают точечные оценки, вычисляемые по выборке, например, методом максимального правдоподобия или методом моментов. Затем по приведенным выше формулам определяют вероятности p_i и величину u.

Критерий согласия состоит в следующем. Если окажется, что u< 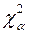, где 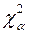– квантиль распределения c², определяемый из соответствующей таблицы при p=a и k=n–l–1, то гипотезу Н₀ о законе распределения принимают, в противном случае – отвергают. При использовании такого правила вероятность отвергнуть гипотезу Н₀ при условии, что она справедлива, равна a.

Задача. Проверить гипотезу о нормальном распределении величины X заработной платы работников определенной отрасли или предприятия на уровне значимости a = 0,05 по выборке объема n =100 человек. Результаты выборочного обследования приведены в табл.7 (интервалы заработной платы – в долларах).

аблица 7

i	[bi-1;bi)	mi	FN(bi-1)	FN(bi)	pi= FN(bi)- -FN(bi-1)	npi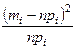
	[190;192)			0,0014	0,1611	0,1597	15,97	0,059
	[192;194)
	[194;196)
	[196;198)		0,1611	0,3745	0,2134	21,34	0,020
	[198;200)		0,3745	0,6366	0,2621	26,21	0,122
	[200;202)		0,6366	0,8437	0,2071	20,71	0,141
	[202;204)			0,8437	0,9987	0,1550	15,5	0,016
	[204;206)
	[206;208)
å	—		—	—	0,9973	99,73	0,358

 

Таблица дополнена вычислениями, производимыми в следующем порядке. Вычисляем оценки математического ожидания и дисперсии по формулам:

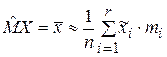
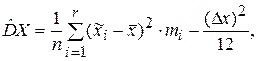
где 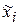– середина i-го интервала r=9 - количество интервалов,

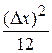– поправка Шеппарда, Dx = 2.

Получаем , , 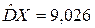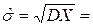3

Для облегчения вычисления величины u объединяем первые три интервала и последние три. Определяем значения функции распределения нормированной случайной величины, используя таблицы функции Лапласа:

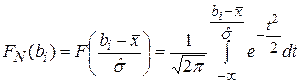(i=0,1,…,5)

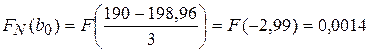
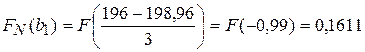
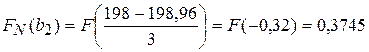
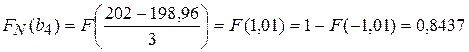
Заполняем всю таблицу и получаем:

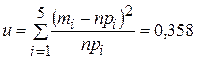
По таблицам для распределения c² при p=a=0,05 и k=5-2-1=2 определяем 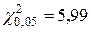. Так как 0,358<5,99, то гипотезу о нормальном распределении зарплаты принимаем, причем в качестве параметров этого распределения берем: а=198,96 и s =3.

5.3. Проверка простых параметрических гипотез

5.3.1. Критерий Неймана-Пирсона для двух простых гипотез

 

Критерий основан на использовании отношения правдоподобия, которое для непрерывных и независимых случайных величин Х₁, Х₂, …, Х_n имеет вид:

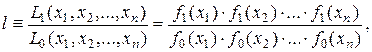
где f₀(x) и f₁(x) – плотности вероятности, соответствующие гипотезам Н₀ и Н₁

Если l <1, то более правдоподобна гипотеза Н₀, а при l >1- гипотеза Н₁

Однако решения принимаются не только исходя из того, какая гипотеза более правдоподобна, но и из других соображений, например, с учетом того, какой экономический ущерб может быть при совершении ошибок в принятии решений. Этот ущерб может быть учтен путем задания значения величины a.

Пусть L₀(x_1,…,x_n) 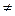0. Тогда для заданного a существует такая константа c= с(a), что условная вероятность Р((l(x_1,…,x_n) > c)/Н₀) = a.

Область 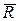в пространстве х₁,…,x_n, выражаемая неравенством l(х₁,…,x_n)>c(a), называется критической областью.

Критерий Неймана-Пирсона в общем случае состоит в следующем. Если выборка x₁,x₂,…,x_n такова что l(х₁,…,x_n) < с(a), то гипотеза Н₀ принимается, в противном случае – отвергается.

Критерий Неймана-Пирсона при заданной вероятности a минимизирует вероятность ошибки второго рода b, которая зависит от гипотезы Н₁. Этот критерий положен, в частности, в основу международных и отечественных стандартов по методам статистического контроля качества продукции.

Пример 1. Пусть имеется выборка х₁,…,x_n из генеральной совокупности, причем известно, что Х~N(a,s² ), т.е. Х распределена по нормальному закону с математическим ожиданием а и дисперсией s². Пусть s известна, основная гипотеза Н₀: а =а₀, а альтернативная Н₁: а=а₁, причем а₁ > a₀. Функция правдоподобия для гипотез Н₀ и Н₁ имеет вид (см. п. 3.3.5.2):

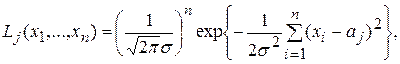где j=0;1

Отношение правдоподобия (после преобразований):

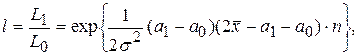
где 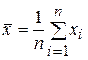– тестовая статистика.

Неравенство l >с равносильно неравенству 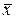>с_a, где c_a – некоторая константа, так как l( 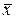) – монотонно возрастающая функция ввиду того, что а₁>а₀, так что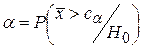

Известно, что если Х~N(a,s² ), то 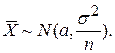Значит

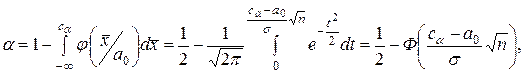
где 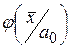– условная плотность вероятности величины 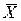(см. рис.18).

 

 

 

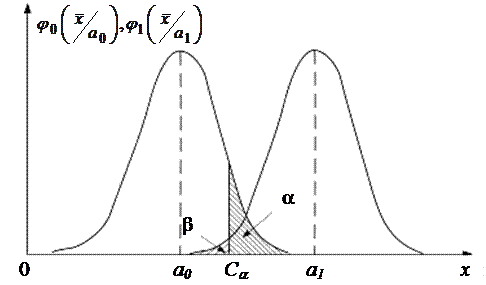
рис. 17

Обозначим 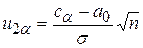. Тогда имеем следующее уравнение:

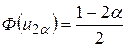
Квантиль u_2α при заданном a находится из таблиц функции Лапласа. И тогда

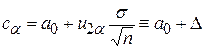
Заметим, что выражение для D совпадает с выражением для половины длины доверительного интервала при доверительной вероятности, равной 1-2a (см. п. 3.4.1).

Правило принятия решения будет следующим: если 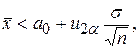то гипотезу H₀ принимают, если 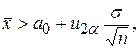то ее отклоняют.

Вероятность ошибки второго рода (см. рис.18):

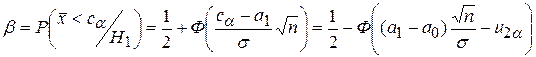
Отсюда можно сделать выводы:

1) величина b уменьшается с ростом a при n=const и с ростом n при a=const

2) при заданных a, b, a₀, a₁ объем выборки находится из условия:

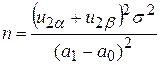
Пример 2. Пусть в примере 1 вместо гипотезы H₁: a=a₁ (a₁>a₀) рассматривается сложная гипотеза H₁: a₁¹a₀. Тогда гипотезу H₀ следует принимать, если:

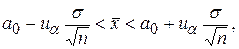
Запишем это выражение иначе:

Но 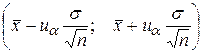– не что иное, как доверительный интервал для математического ожидания MX при доверительной вероятности 1-a. Значит, правило принятия решения можно сформулировать иначе: если величина a₀ окажется в пределах построенного доверительного интервала, то H₀ принимают, в противном случае – отклоняют.

Здесь использование вероятности b бессмысленно, так как при a₁¹a₀, сколь угодно близком к a₀, получаем b=1–a/2, т.е. слишком большое число.

Пример 3. Пусть имеется выборка х₁,…,x_n, где x_i=0 или x_i=1 при любом i, причем все Х_i независимы и имеют распределение Бернулли с одной и той же вероятностью p = P(X_i=1). Пусть гипотезы H₀: p=p₀, H₁: p=p₁, причем p₁>p₀.

Функции правдоподобия для гипотез H₀ и H₁ имеют вид:

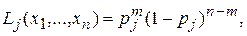если в выборке m единиц (остальные – нули).

Отношение правдоподобия:

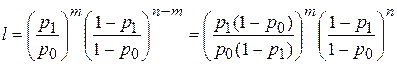
Неравенство l>c можно заменить неравенством m>c_a, так как l(m) – возрастающая функция, так что

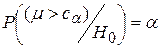
Величина m распределена по биномиальному закону:

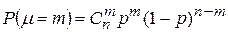
Поэтому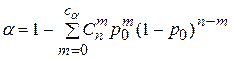

Искомая величина c_a является корнем этого уравнения. Но поскольку c_a=0,1,2,…, то может оказаться, что это равенство, строго говоря, не выполняется. Тогда надо брать такое 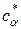, при котором правая часть уравнения окажется меньше заданного a, при условии, что при c_a= 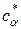- 1 правая часть больше a. Величина 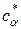определяется численными методами.

Если заданы величины p₀, p₁, a, b, то объем выборки n и границу 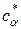находят из системы уравнений:

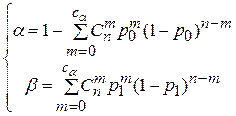
В литературе, международных и отечественных стандартах по методам статистического контроля качества продукции приведены таблицы для определения n и 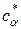. Там p – доля дефектных изделий в партии, 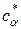– контрольный норматив (приемочное число), a и b называют рисками поставщика и потребителя соответственно, p₀ и p₁ – соответственно приемочным и браковочным уровнями дефектности. Если число дефектных изделий в выборке m£ 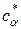, партию продукцию принимают, в противном случае бракуют.

В социологических исследованиях для решения задач проверки гипотез относительно вероятности p₀ часто используют вместо биномиального распределения величины m нормальное с математическим ожиданием np₀ и дисперсией np₀(1-p₀). Однако такую замену можно осуществлять только при np₀(1-p₀)>9.

адача 1.

В функции налоговой инспекции входит проверка закрепленных за ней предприятий с целью выявления фактов сокрытия доходов от налогообложения. Предположим, ни один такой факт не является допустимым и при тотальной проверке предприятия можно вскрыть все факты сокрытия доходов. Однако налоговая инспекция предпочитает производить сначала выборочные проверки: из N осуществленных торговых сделок проверять только п, причем п<0,1·N. По результатам выборочной проверки может быть принято одно из двух решений: проверку прекратить (если не установлено ни одного факта сокрытия доходов) или произвести тотальную проверку.

Пусть налоговая инспекция считает не допустимым, чтобы уходили от ответственности предприятия, осуществляющие не менее 20% своих торговых сделок с сокрытием доходов. Необходимо:

а) определить при п=8 и п=16 вероятности ошибок при принятии решений:

a – вероятность перехода к тотальной проверке законопослушного предприятия,

b – вероятность не разоблачения предприятия, осуществляющего 20% своих торговых сделок с сокрытием доходов от налогообложения;

б) определить объем выборки n при заданном b=0,1.

Переведем эту задачу на язык задачи проверки гипотез (см. пример 3). У нас р - доля торговых сделок с сокрытием доходов. Гипотезы: Н₀ – предприятие законопослушное, Н₁ – предприятие скрывает доходы, причем Н₀: р=р₀=0, Н₁: р=р₁=0,2. Тестовая статистика m – число сделок (в выборке объема n) с сокрытием доходов. Решения четко соответствуют принятию или отклонению гипотезы Н₀, т.е. правило принятия гипотезы Н₀ (ввиду того, что р₀=0) очевидно: при m=0 Н₀ принимается, а при m>0 – отклоняется. Иначе говоря, c_a=0. И тогда очевидно, что a=Р((m>0)/H₀)=0. Остается одна вероятность b.

Тестовая статистика, как случайная величина, распределена приблизительно по биномиальному закону. Значит:

b = (1-р₁)ⁿ = 0,8ⁿ

Отсюда можно определить b при заданном n либо n при заданном b:

n = log_0,8b = lgb / lg0,8

а) При п=8 имеем b=0,8⁸=0,168, при п=16 b=0,8¹⁶=0,028.

б) При b=0,1 имеем п=lg0,1/ lg0,8 = -1/ -0,097» 10,3

Округляем n в сторону увеличения, чтобы обеспечить b<0,1. Тогда п=11, b(11)=0,8¹¹=0,086.

Таким образом, если брать выборку п=11, то примерно каждые 9 предприятий из 100, осуществляющих 20% своих сделок с сокрытием доходов, не будут разоблачены.

адача 2.

Внесем небольшое изменение в условие задачи 1. Предположим, налоговая инспекция считает допустимым, что не более 2% сделок на предприятии осуществляется с сокрытием доходов от налогообложения. Возьмем р₀=0,02. По-прежнему c_a=0. Вычислим a для п=8 и п=11.

Очевидно a=1-(1-р₀)ⁿ =1-0,98ⁿ

При п=8 имеем a=1-0,98⁸=0,15, при п=11 a=1-0,98¹¹=0,20

Таким образом, при объеме выборки n =11 в среднем каждое пятое законопослушное, но работающее на грани дозволенного предприятие будет подвергаться тотальной проверке.

5.3.2. Критерий Байеса для двух простых гипотез и другие критерии

 

Критерий Байеса основан на предположениях, что гипотезы являются случайными событиями и известны априорные вероятности гипотез: p₀=P(H₀), p₁=P(H₁)=1-p₀ (не путать с обозначениями в предыдущем примере 3), а также известна матрица потерь (ее называют платежной матрицей):

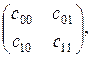
где c_ij – потери (обычно, экономические) в результате принятия гипотезы H_i в то время как справедлива гипотеза H_j. Потери c₀₀ и c₁₁ от принятия правильных решений обычно имеют знак минус. Их модуль равен выигрышу (доходу).

В соответствии с критерием Байеса, при получении значения тестовой статистики t (в частности, t – среднее арифметическое), определяемой по выборке объема n, необходимо принимать гипотезу H₀, если выполняется неравенство:

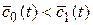или g(t)≡ 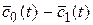<0,

где 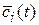– апостериорные средние потери в случае принятия гипотезы H_i (i=0;1):

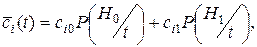
g(t)=0 – граница, отделяющая области принятия G и отклонения 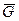гипотезы Н₀, 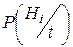– апостериорная вероятность гипотезы H_i, определяемая по формуле Байеса, которая для непрерывной тестовой статистики имеет вид:

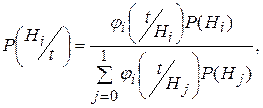i=0;1,

где 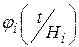– условная плотность вероятности тестовой статистики T (при условии справедливости гипотезы H_i), вид и параметры которой определяются через информацию о плотностях 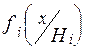≡ f_i (x).

Условие принятия гипотезы Н₀ после подстановки формул имеет вид:

или .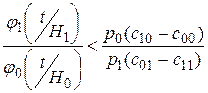

Для дискретной случайной величины Т в формулах должна стоять вероятность 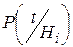вместо .

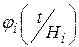Потери с_ij, вообще говоря, часто зависят от t, но, как правило, такая зависимость слабая, поэтому их обычно считают величинами постоянными.

Все формулы справедливы, если под t понимать вектор тестовых статистик, например, среднее арифметическое 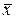и оценку среднего квадратического отклонения – s. Тогда 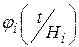– многомерная плотность вероятности.

Вычисление величин потерь требует выбора начала отсчета. Поэтому иногда выбирают c₀₀=0 и c₁₁=0, а c₁₀ и c₀₁ оценивают относительно c₀₀ и c₁₁ соответственно. Все 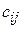следует оценивать из анализа планируемых решений после принятия гипотез, а также возможных последствий. Потери 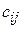часто вычисляют как математические ожидания в других вероятностных пространствах.

При c₀₀=0, c₁₁=0, c₁₀=c₀₁ условие принятия гипотезы Н₀ имеем вид:

.

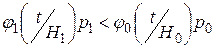Этот критерий равносилен критерию максимума апостериорной вероятности

,

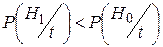в соответствии с которым принимается та гипотеза, апостериорная вероятность которой больше.

Если к тому же р₁=р₀ , то получим неравенство, равносильное критерию максимума правдоподобия l <1 (см. п. 5.3.1.), при условии, что вектор тестовых статистик t является исчерпывающим для видов распределений f_i (x) (i=0;1).

Вместо матрицы потерь часто используют матрицу выигрышей: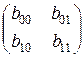

Тогда правило принятия гипотезы Н₀: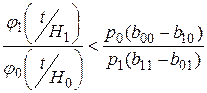

Для конкретных видов распределений f_i(x) все эти правила можно получить в более простом виде. В частности, если распределения нормальные с известными дисперсиями, то тестовой статистикой t будет среднее арифметическое 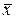и правило принятия гипотезы Н₀ запишется в виде квадратного неравенства. Один или два корня квадратного уравнения будут границами области G.

Критерий Байеса, вообще говоря, – это критерий минимума средних потерь (или максимума среднего выигрыша), т.е. математического ожидания потерь. В задачах проверки простых гипотез он выглядит следующим образом:

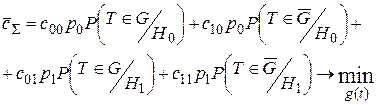
Иначе говоря, граница g(t)=0 между областями принятия и отклонения гипотезы H₀ должна задаваться таким образом, чтобы суммарные средние потери от принятия решений (если предположить, что аналогичные ситуации будут повторяться) были минимальны. Произведем в данном выражении замену:

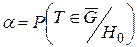, 1– a= 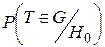, b= 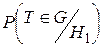, 1– b= .

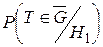Заметим, что условные вероятности ошибок I и II рода a и b в общем случае являются функциями от функции g(t), т.е. функционалами. После преобразований и отбрасывания постоянных величин критерий Байеса может быть записан в виде так называемого критерия минимума среднего риска (средних потерь по сравнению с правильными решениями):

Величины p₀×a=a_б и p₁×b=b_б называют безусловными вероятностями ошибок первого и второго рода.

Заменяя в этом выражении

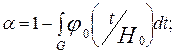
и отбрасывая постоянную, получим:

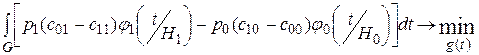
Минимум этого функционала достигается в случае, если подынтегральное выражение меньше нуля, т.е.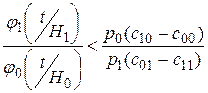

Получили условие принятия гипотезы Н₀, выведенное прежде.

Замечание. Использование простых гипотез во многих практических ситуациях приводит к слишком грубым правилам принятия решений. Причина состоит в том, что порой трудно решить, каким состояниям системы должны соответствовать гипотезы H₀ и H₁. Например, при какой доле дефектных изделий партию продукции следует считать удовлетворительного качества, а при какой – неудовлетворительного? А условные плотности вероятности тестовой статистики T, а значит, и правило принятия решений, сильно зависят от того, что принять за H₀ и H₁. В таких ситуациях можно перейти к использованию сложных гипотез, т.е. к непрерывным множествам возможных состояний системы. Тогда область возможных значений параметра h можно разбить на две области S₀ и S₁, одна из которых соответствует гипотезе H₀, другая – гипотезе H₁ (область S₁ в случае двухстороннего ограничения на значения параметра будет неодносвязанной). Можно выделить и три односвязанные области. Вместо вероятностей 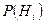должны быть известны плотности распределения w_i(h).

Однако применение сложных гипотез далеко не всегда позволяет улучшить правила принятия решений. Потери с_ij от принятия гипотезы H_i в то время как справедлива гипотеза H_j часто получаются слишком усредненными. Применение теории проверки гипотез не позволяет учитывать потери как функцию от h. В распространенном частном случае, как уже отмечалось в подразделе 5.1., когда альтернативная сложная гипотеза H₁ есть логическое отрицание основной сложной гипотезы H₀, легче бывает оценить априорное распределение w(h) параметра h, чем распределения w₀(h) и w₁(h). Аналогично обстоит дело и в том случае, если имеется 3 гипотезы, составляющее полную группу событий, или более. Тогда надо вообще отказаться от применения теории проверки гипотез и для решения практической задачи использовать теорию статистических решений.

5.4. Дисперсионный анализ

 

Дисперсионный анализ является одним из методов статистического анализа и используется для выявления влияния факторов, являющихся качественными признаками (т.е. параметрами, измеряемыми в шкале наименований), на характеристики некоторой случайной величины Y. Например, – для выявления влияния способа рекламирования товара на объем его продаж; места торговой точки на цену продукции; технологии производства продукции или услуг на некоторый показатель качества продукции или услуг. В этом случае будет иметь место однофакторный дисперсионный анализ. Если же изучается, например, не только влияние технологии, но и уровень квалификации персонала, то будет иметь место двухфакторный дисперсионный анализ.

В дисперсионном анализе имеют дело со сгруппированными данными (см. п.п. 3.3.2.; 3.3.3.), точнее – с расслоенной выборкой. При этом каждый слой соответствует определенному значению некоторого качественного признака j (j =1,2,3,…, d). Качественный признак называется фактором, а его значение – уровнем фактора. Таким образом, расслоенная выборка – это совокупность всех случайных выборок, каждая из которых получена при определенном (фиксированном) значении уровня фактора. При однофакторном анализе выборка является расслоенной по одному фактору. При двухфакторном – по двум, т.е. имеется два способа расслоения. Однофакторный анализ используется для двух ситуаций. В первой уровни фактора фиксируются заранее (например, способ рекламирования товара). Во второй ситуации уровни фактора являются случайной выборкой из генеральной совокупности уровней фактора (например, мест торговли). Двухфакторный анализ кроме этих двух ситуаций используется еще и в смешанной ситуации.

Оценка влияния фактора на характеристики случайной величины Y производится методами проверки параметрических гипотез, когда альтернативная гипотеза H₁ является логическим отрицанием основной простой гипотезы H₀, т.е. H₁ = 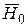. При этом вводится в рассмотрение только условная вероятность ошибки первого рода a. Гипотезы проверяются по отношению как к дисперсиям, так и к математическим ожиданиям случайной величины Y внутри каждого слоя. В результате обычно получают ответ на главный вопрос: можно ли рассматривать (и насколько уверенно) все выборки из слоев как случайные выборки из одной генеральной совокупности значений случайной величины Y. Если можно, то это как раз и означает, что влиянием факторов можно пренебречь. В противном случае оценивают степень влияния каждого фактора.

Здесь рассмотрим только однофакторный дисперсионный анализ. Сначала рассмотрим первую ситуацию. Пусть фактор j имеет d уровней. Уровень j (j=1,2,3,…d) будем характеризовать величиной смещения ∆ _j = а_j – MY, где а_j≡MY_j и MY – математические ожидания случайных величин Y_j и Y в j -м слое и во всей генеральной совокупности соответственно, а также дисперсией 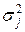случайной величины Y_j в j -м слое. Тогда модель зависимости между случайной величиной Y и фактором j можно записать в виде:

Y(j)≡ Y_j = MY+ ∆ _j + ε_j, где ε_j