1. Номер варианта контрольной работы соответствует порядковому номеру в учебной ведомости (уточняется преподавателем на аудиторных занятиях).
2. Сборник контрольных работ содержит 30 вариантов. Студенты, имеющие порядковые номера 31-й, 32-й и т.д. выполняют варианты контрольной работы, начиная с первых номеров, т.е. №1, №2 и т.д.
3. В каждой контрольной работе 5 (пять) задач: три – по теории вероятностей, две – по математической статистике. Контрольная работа принимается к проверке преподавателем при решении всех пяти задач. В противном случае работа возвращается студенту для выполнения КР в полном объеме.
4. Контрольные работы принимаются как в печатном (А4), так и в рукописном виде с подробным пояснением выполняемых действий и используемых формул и положений.
5. В любом случае контрольная работа оформляется с титульным листом соответствующей формы.
6. После проверки контрольная работа возвращается студенту для устранения замечаний и дополнительной подготовки к защите. Исправленная работа выносится на защиту.
Варианты контрольной работы
| Вариант 1 | |
| 1/3 ламп производится на первом заводе, 1/4 – на втором, остальные – на третьем. Вероятности брака в продукции первого, второго и третьего заводов соответственно равны 0,2, 0,15 и 0,05. Найдите вероятность того, что бракованная лампа произведена на первом, втором или третьем заводе. | |
| Телефонная станция обслуживает 1000 абонентов. В течение часа любой абонент независимо от остальных может сделать вызов с вероятностью 0,005. Требуется найти вероятность того, что в течение часа было не более 7 вызовов. | |
Случайная величина Х задана интегральной функцией
 Найти:
а) дифференциальную функцию
Найти:
а) дифференциальную функцию 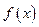 (плотность вероятности);
б) математическое ожидание и дисперсию величины X;
в) вероятность того, что X примет значение, принадлежащее интервалу (плотность вероятности);
б) математическое ожидание и дисперсию величины X;
в) вероятность того, что X примет значение, принадлежащее интервалу 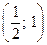 ;
г) построить графики функций ;
г) построить графики функций  и и 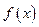 . .
| |
| Администрацию универсама интересует оптимальный уровень запасов продуктов в торговом зале, а также среднемесячный объем покупок товаров, не являющихся предметом ежедневного потребления в семье (таких, например, как сода). Для выяснения этого вопроса менеджер универсама в течение января регистрировал частоту покупок стограммовых пакетиков с содой и собрал следующие данные (хi): 8, 4, 4, 9, 3, 3, 1, 2, 0, 4, 2, 3, 5, 7, 10, 6, 5, 7, 3, 2, 9, 8, 1, 4, 6, 5, 4, 2, 1, 0, 8. Постройте вариационный ряд, определите его числовые характеристики (Выборочное среднее арифметическое, выборочная дисперсия, выборочное среднее квадратическое отклонение, мода, медиана, коэффициент вариации). Какие рекомендации вы дали бы администрации универсама? | |
| Среди стандартных изделий одной фабрики в среднем 15% относится ко второму сорту. С какой вероятностью можно утверждать, что процент изделий второго сорта среди 1000 стандартных изделий данной фабрики отличается от 15% по абсолютной величине меньше чем на 2%? |
| Вариант 2 | |||||||||||
| Брокерская компания проводит операции с ценными бумагами: 10% сделок заключается с инвестиционными банками, 20% – с другими брокерскими компаниями, остальные – с физическими лицами. Вероятности того, что контрагент не выполнит условия сделки, составляют для указанных групп контрагентов 0,01, 0,05 и 0,2 соответственно. Определить, какая доля сделок в среднем не исполняется по вине контрагентов. | |||||||||||
| Среди работников компании каждый пятый имеет высшее образование. Найти вероятность того, что среди наудачу отобранных 4-х работников компании, хотя бы два имеют высшее образование. | |||||||||||
Случайная величина X имеет распределение, заданное таблицей
Составить закон распределения, найти математическое ожидание и дисперсию случайной величины | |||||||||||
Для оценки состояния деловой активности промышленных предприятий различных форм собственности были проведены выборочные бизнес-обследования и получены следующие результаты:
Постройте гистограмму распределения частот. Найдите среднее значение показателя деловой активности, дисперсию, среднее квадратическое отклонение, коэффициент вариации. Объясните полученные результаты. | |||||||||||
| Служба контроля энергосбыта провела выборочную проверку расхода электроэнергии жителями одного из многоквартирных домов. С помощью собственно-случайного отбора выбрано 10 квартир и определен расход электроэнергии в течение одного из летних месяцев (кВт ч): 125; 78; 102; 140; 90; 45; 50;125; 115;112. С вероятностью 0,95 определите доверительный интервал для оценки среднего расхода электроэнергии на 1 квартиру во всем доме при условии, что в доме 70 квартир, а отбор был: а) повторным; б) бесповторным. |
| Вариант 3 | |||||||||||||||
| Была проведена одна и та же контрольная работа в трех группах. В первой группе из 30 студентов 8 выполнили работу на «отлично», во второй, где 28 студентов, – 6 «отличных» работ, в третьей, где 27 студентов, – 9 работ выполнены на «отлично». Найти вероятность того, что первая выбранная наудачу работа из работ, принадлежащих группе, которая также выбрана наудачу, окажется «отличной». | |||||||||||||||
| При установке газовой плиты вероятность того, что она не потребует ремонта в течение гарантийного срока 0,9. Найти вероятность, что из четырех установленных в коттедже газовых плит, не более чем одной потребуется ремонт в течение гарантийного срока. | |||||||||||||||
Случайная величина X задана функцией распределения
 Найти постоянную C, математическое ожидание квадрата случайной величины X и дисперсию случайной величины X, построить графики функция f (x), F (x).
Найти постоянную C, математическое ожидание квадрата случайной величины X и дисперсию случайной величины X, построить графики функция f (x), F (x).
| |||||||||||||||
Имеются выборочные данные о стоимости потребительской корзины из 19 основных продуктов по городам N-ой области (на начало 2012 г.).
Постройте полигон распределения частот. Найдите среднюю стоимость потребительской корзины в выборке, дисперсию, среднее квадратическое отклонение, коэффициент вариации. Объясните полученные результаты. | |||||||||||||||
Результат обследования 100 рабочих крупного завода, проводимого с целью определения времени, затрачиваемого на обработку детали, приведены в таблице
Найти границы, в которых с надежностью 0,95 заключено среднее время обработки детали. |
| Вариант 4 | |||||||||||
| В библиотеке имеется 5 методичек выпуска 2007 года и 9 методичек по той же теме выпуска 2012 года. Библиотекарь выдает на группу 6 методичек. Какова вероятность того, что первой пришедшей группе будет выдано 5 методичек выпуска 2012 года, если библиотекарь берет методички произвольно? | |||||||||||
| При передаче сообщения вероятность искажения каждого знака равна 0,01. Предполагая независимость искажения любого из знаков, найти вероятность того, что группа из 5 знаков: а) не будет искажена; б) будет содержать менее двух искажений. | |||||||||||
Случайная величина X задана плотностью вероятности
 Найти:
а) значение параметра a;
б) функцию распределения F (x);
в) вероятность попадания случайной величины X в интервал
Найти:
а) значение параметра a;
б) функцию распределения F (x);
в) вероятность попадания случайной величины X в интервал 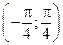 ;
г) построить графики f (x), F (x). ;
г) построить графики f (x), F (x).
| |||||||||||
Имеются выборочные данные о числе сделок, заключенных брокерскими фирмами и конторами города в течение месяца.
Постройте гистограмму распределения частот. Найдите среднее число заключенных сделок, дисперсию, среднее квадратическое отклонение, коэффициент вариации, размах вариации. Объясните полученные результаты. | |||||||||||
| Размер некоторой детали измерялся 8 раз. Результаты измерений в мм таковы: 5,4; 5,0; 4,8; 4,9; 5,2; 5,3; 5,2; 5,0. Зная, что ошибки измерений следуют нормальному закону, найти: а) вероятность получения случайного результата измерений в пределах полученных при измерениях результатов; б) доверительный интервал для оценки математического ожидания с надежностью 0,99; в) доверительный интервал для оценки средней квадратической ошибки с надежностью 0,95. |
| Вариант 5 | |||||||||||||
| В партии из 20 изделий 5 изделий имеют скрытый дефект. Какова вероятность того, что из взятых наугад 4 изделий 2 изделия являются дефектными. | |||||||||||||
| По многолетним наблюдениям в районе обсерватории из 30 ноябрьских ночей ясными бывают, в среднем, 10 ночей. Группе астрономов, собирающихся сделать мировое открытие, выделено 5 ночей для наблюдений. Найти вероятность того, что мировое открытие будет совершено, если для этого потребуется, по крайней мере, 2 ясные ночи. | |||||||||||||
Случайная величина X задана интегральной функцией (функцией распределения)
 .
Найти:
а) математическое ожидание случайной величины X (ответ записать в виде десятичной дроби приближённо с точностью до 0,01);
б) вероятность попадания значений X в интервал (0, 3).
в) построить графики функций .
Найти:
а) математическое ожидание случайной величины X (ответ записать в виде десятичной дроби приближённо с точностью до 0,01);
б) вероятность попадания значений X в интервал (0, 3).
в) построить графики функций  и и 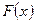 . .
| |||||||||||||
Имеются данные о годовой мощности предприятий в 2003 году
а) Постройте гистограмму, кумуляту. б) Рассчитайте среднюю мощность предприятий. в) Найдите дисперсию, среднее квадратическое отклонение, коэффициент вариации. г) Сделайте анализ полученных результатов. | |||||||||||||
Произведено измерение некоторого размера у 25 деталей. При обработке результатов измерений, следующих нормальному закону, найдено: 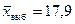 мм, мм, 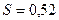 .
Определить:
а) вероятность получения случайного результата в пределах от 18 до 19 мм;
б) доверительный интервал для оценки математического ожидания с надежностью 0,99 с применением нормального распределения;
в) доверительный интервал для оценки среднего квадратического отклонения с надежностью 0,95. .
Определить:
а) вероятность получения случайного результата в пределах от 18 до 19 мм;
б) доверительный интервал для оценки математического ожидания с надежностью 0,99 с применением нормального распределения;
в) доверительный интервал для оценки среднего квадратического отклонения с надежностью 0,95.
|
| Вариант 6 | |||||||||||
| В первом ящике находится 5 белых и 3 черных шара, а во втором – 3 белых и 5 черных. Из первого ящика перекладывают во второй наугад два шара, а затем берут из второго один шар. Какова вероятность того, что этот шар окажется черным. | |||||||||||
| Найти вероятность наступления события A ровно 3 раза в 5 независимых испытаниях, если вероятность появления этого события в каждом испытании равна 1/3. Определить также вероятность наступления события A не менее 4 раз в этих же условиях. | |||||||||||
| Сделано два высокорисковых вклада: 10 тыс. руб. в компанию A и 15 тыс. руб. в компанию B. Компания A обещает 20% годовых, но может «лопнуть» с вероятностью 0,1. Компания B обещает 10% годовых, но может «лопнуть» с вероятностью 0,05. Составить закон распределения случайной величины – общей суммы прибыли (убытка), полученной от двух компаний через год, определить ожидаемую доходность и уровень риска. | |||||||||||
Имеются данные о группировке коммерческих банков РФ по величине объявленного уставного фонда (на 1 марта 2009 г.).
Постройте гистограмму распределения частот. Найдите средний размер объявленного уставного фонда коммерческих банков РФ. Охарактеризуйте колеблемость размера объявленного уставного фонда коммерческих банков с помощью соответствующих показателей. | |||||||||||
При просмотре 10000 волокон из партии льна обнаружено 1200 недозрелых. Сколько надо просмотреть волокон льна из этой партии, чтобы с вероятностью 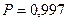 можно было ручаться за точность определения доли недозрелых волокон во всей партии в пределах 1%? Отбор бесповторный. можно было ручаться за точность определения доли недозрелых волокон во всей партии в пределах 1%? Отбор бесповторный.
|
| Вариант 7 | |||||||||||||||||||||||||||
| В пирамиде пять винтовок, три из которых снабжены оптическим прицелом. Вероятность того, что стрелок поразит мишень при выстреле из винтовки с оптическим прицелом, равна 0,95; для винтовки без оптического прицела эта вероятность равна 0,7. Найти вероятность того, что мишень будет поражена, если стрелок произведет один выстрел из наудачу взятой винтовки. | |||||||||||||||||||||||||||
| На факультете учатся 500 студентов. Найти вероятность того, что первое сентября является днем рождения: а) трех студентов; б) не менее трех. | |||||||||||||||||||||||||||
| Сделано два высокорисковых вклада: 10 тыс. руб. в компанию A и 15 тыс. руб. в компанию B. Компания A обещает 10% годовых, но может «лопнуть» с вероятностью 0,5. Компания B обещает 5% годовых, но может «лопнуть» с вероятностью 0,25. Составить закон распределения случайной величины – общей суммы прибыли (убытка), полученной от двух компаний через год, определить ожидаемую доходность и уровень риска. | |||||||||||||||||||||||||||
Имеются данные о денежной эмиссии, осуществлявшейся ЦБ РФ в период 2001-2004 гг.
Найдите среднегодовой размер эмиссии за указанный период. Охарактеризуйте колеблемость размера эмиссии с помощью различных показателей вариации. | |||||||||||||||||||||||||||
При изучении физико-механических свойств обувных кож испытано n = 12 образцов и получены следующие значения предела прочности кожи на разрыв X, Н/мм:
Требуется: а) выполнить первичную статистическую обработку результатов наблюдений, т.е. определить выборочное среднее б) полагая, что изменчивость величины признака X описывается законом нормального распределения, найти доверительный интервал для среднего предела прочности a этой кожи на уровне заданной надежности γ = 0,90. |
| Вариант 8 | |||||||||||||
| В телеателье имеется три кинескопа. Вероятности неисправности каждого из них соответственно равны 0,1; 0,2; 0,1. Какова вероятность того, что среди этих кинескопов исправными окажутся: а) два кинескопа; б) хотя бы один кинескоп. | |||||||||||||
| Имеется 4 колоды карт по 36 листов. Из каждой колоды извлекают по одной карте. Какова вероятность, что среди извлеченных карт 3 картинки? | |||||||||||||
| Производится три выстрела по мишени. Вероятность попадания при каждом выстреле равна 0,4. Рассматривается случайная величина X – число попаданий при трех выстрелах. Построить ряд распределения и функцию распределения случайной величины X. Найти ее математическое ожидание, дисперсию, среднее квадратическое отклонение. | |||||||||||||
| Имеются данные о еженедельном количестве проданных компьютеров одной из фирм: 398, 412, 560, 474, 544, 690, 587, 600, 613, 457, 504, 477, 530, 641, 359, 566, 452, 633, 474, 499. 580, 606, 344, 455,505, 396, 347, 441, 390, 632, 400, 582. Составьте вариационный ряд. Найдите среднее количество проданных компьютеров. Рассчитайте показатели вариации (Выборочное среднее арифметическое, выборочная дисперсия, выборочное среднее квадратическое отклонение, мода, медиана, коэффициент вариации). | |||||||||||||
При выборочном обследовании физического веса готовой продукции по схеме бесповторного собственно-случайного отбора получены следующие результаты:
Найти доверительные границы для генерального среднего, отвечающие вероятности |
| Вариант 9 | |||||||||||||
| В тире имеется пять винтовок, вероятности попадания из которых соответственно равны 0,5, 0,6, 0,7, 0,8 и 0,9. Стрелок берет наудачу одну из винтовок. Найти вероятность попадания в цель. | |||||||||||||
| Имеется 2 урны. В первой урне 5 белых и 5 черных шаров. Во второй урне 3 белых и 2 черных шара. Наудачу выбирается урна и из нее вынимается шар. Затем шар возвращается в урну, из которой его вынули, и процедура повторяется еще 5 раз (всего процедура проведена 6 раз). Какова вероятность того, что число вынутых белых шаров будет: а) три; б) более трех. | |||||||||||||
По заданному закону распределения дискретной случайной величины X найти ее среднее квадратическое отклонение, получить функцию распределения F (x), привести аналитическое и графическое изображение функции распределения F (x), построить многоугольник распределения вероятностей.
| |||||||||||||
| Имеются данные о числе тонн грузов, перевозимых еженедельно паромом некоторого морского порта в период навигации: 398, 412, 560, 474, 544, 690, 587, 600, 613, 457, 504, 477, 530, 641, 359, 566, 452, 633, 474, 499, 580, 606, 344, 455, 505, 396, 347, 441, 390, 632, 400, 582. а) Составьте вариационный ряд. б) Рассчитайте показатели вариации ряда (Выборочное среднее арифметическое, выборочная дисперсия, выборочное среднее квадратическое отклонение, мода, медиана, коэффициент вариации). в) Сделайте анализ полученных результатов. | |||||||||||||
По схеме повторной выборки произведено выборочное измерение выработки на земляных работах у 145 рабочих. В результате этого обследования средняя выработка определена в 4,95 м3 на одного рабочего, а среднее квадратическое отклонение оказалось равным 1,5 м3. Найти доверительные границы для генерального среднего, отвечающие вероятности  . .
|
| Вариант 10 | |||||||||||||||||
| В урне 3 белых и 7 черных шаров. Какова вероятность того, что вынутые наугад два шара окажутся белыми? | |||||||||||||||||
| Известно, что 30% призывников имеют 27 размер обуви. Сколько пар обуви надо иметь на складе воинской части чтобы с вероятностью р0=0,9 были обеспечены все такие призывники, если в часть прибыло 200 новобранцев. | |||||||||||||||||
По заданному закону распределения дискретной случайной величины X найти ее среднее квадратическое отклонение, получить функцию распределения F (x), привести аналитическое и графическое изображение функции распределения F (x), построить многоугольник распределения вероятностей.
| |||||||||||||||||
Кредиты ЦБ РФ предприятиям России за 7 месяцев 2012 г. (с апреля по октябрь) характеризуются следующими данными:
Найдите среднемесячный размер кредита за указанный период. Охарактеризуйте колеблемость размеров кредита с помощью соответствующих показателей. | |||||||||||||||||
По результатам семи измерений средняя высота сальниковой камеры равна 40 мм, а S= 1,8 мм. В предположении о нормальном распределении определить вероятность того, что генеральная средняя будет внутри интервала 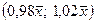 . .
|
| Вариант 11 | |||||||||||||
| В урне 4 белых и 6 черных шаров. Из урны наудачу извлечены 2 шара. Найти вероятность того, что они разного цвета. | |||||||||||||
| Завод отправил на базу 500 изделий. Вероятность повреждения изделия в пути равна 0,002. Найти вероятность того, что в пути будет повреждено изделий: а) ровно три; б) менее трех; в) более трех; г) хотя бы одно. | |||||||||||||
По заданному закону распределения дискретной случайной величины X, найти ее среднее квадратическое отклонение, привести аналитическое и графическое изображение функции распределения F (x), построить многоугольник распределения вероятностей.
| |||||||||||||
Найти числовые характеристики выборки, заданной таблицей (Выборочное среднее арифметическое, выборочная дисперсия, выборочное среднее квадратическое отклонение, мода, медиана, коэффициент вариации)
| |||||||||||||
| По выборке объемом 25 единиц определена выборочная средняя диаметров поршневых колец. В предложении о нормальном распределении найти с надежностью γ= 0,975 точность δ, с которой выборочная средняя оценивает математическое ожидание, зная, что среднее квадратическое отклонение поршневых колец равно 4 мм. |
| Вариант 12 | |||||||||||
| В урне находится 12 шаров: 8 белых и 4 красных. Какова вероятность того, что выбранные наугад два шара будут одного цвета. | |||||||||||
| Для данного баскетболиста вероятность забросить мяч в корзину при одном броске 0,5. Произведено 6 бросков. Найти вероятность того, что попаданий будет больше половины. | |||||||||||
Плотность распределения случайной величины
 Найти параметр a, функцию распределения и F (x) и вероятность
Найти параметр a, функцию распределения и F (x) и вероятность  . Построить графики функций . Построить графики функций  и и 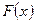 . .
| |||||||||||
Найти числовые характеристики выборки, заданной таблицей (Выборочное среднее арифметическое, выборочная дисперсия, выборочное среднее квадратическое отклонение, мода, медиана, коэффициент вариации)
| |||||||||||
| Партия изделий считается годной к выпуску, если брак в ней не превышает 3%. Из партии в 2000 изделий было отобрано и проверено 400. При этом бракованных изделий оказалось 6. Какова вероятность того, что вся партия удовлетворяет техническим условиям и может быть принята? |
| Вариант 13 | |||||||||||||||||||||||||
| В цехе работают три станка. Вероятность отказа в течение смены для станков соответственно равна 0,1, 0,2 и 0,15. Найти вероятность того, что в течение смены безотказно проработают два станка. | |||||||||||||||||||||||||
| Выход молодняка в инкубаторе составляет в среднем 75% числа заложенных яиц. Оценить вероятность того, что из 8000 заложенных в инкубатор яиц вылупится от 5950 до 6050 (включительно) яиц. | |||||||||||||||||||||||||
Обзор счетов 400 инвесторов на фондовой бирже дал следующую информацию о числе сделок в течение последнего квартала:
1. Постройте график распределения X. 2. Найдите вероятность того, что случайно выбранный инвестор произвел: - ноль сделок; - по крайней мере, одну сделку; - больше пяти; - меньше шести. 3. Найдите математическое ожидание и дисперсию числа сделок. | |||||||||||||||||||||||||
Найти числовые характеристики выборки, заданной таблицей (Выборочное среднее арифметическое, выборочная дисперсия, выборочное среднее квадратическое отклонение, мода, медиана, коэффициент вариации)
| |||||||||||||||||||||||||
Определить численность выборки при обследовании остатков на расчетных счетах у клиентов Госбанка, чтобы с вероятностью 0,683 ошибка репрезентативности не превышала 5 руб., если  руб. руб.
|
| Вариант 14 | |||||||||||||||
| Два производственных участка по выпуску однотипной продукции за смену выдали одинаковое количество изделий. Возможный процент брака на первом участке составляет 5%, на втором – 4%. Найти вероятность того, что наудачу взятая деталь, из числа поступивших на склад, не соответствует установленным требованиям. | |||||||||||||||
| Всхожесть семян новой культуры 85%. На опытном участке посеяли 500 семян. Найти вероятность того, что прорастут от 400 до 450 семян. | |||||||||||||||
| Непрерывная случайная величина Х распределена равномерно на отрезке [2, 6]. Какова вероятность принятия ею значений, не более, чем на 0,5 отклоняющихся от среднего значения? | |||||||||||||||
Ниже представлена группировка отраслей и подотраслей промышленности по темпам роста цен на изготавливаемую продукцию за период с начала года.
Найдите среднюю арифметическую, дисперсию, среднее квадратическое отклонение, коэффициент вариации. Постройте гистограмму. Сделайте выводы. | |||||||||||||||
Из партии изделий объемом в 2000 штук сформирована выборка размером 110 единиц, распределение которых по значению признака X дается следующей таблицей:
Определить: а) Пределы, в которых с вероятностью 0,954 заключено среднее значение величины X; б) Вероятность того, что доля признака Y для X не менее 1500, во всей совокупности, отличается от выборочной доли не более чем на 0,05 (по абсолютной величине). |
| Вариант 15 | |||||||||||||||||||||||||
| Есть три завода,производящих одну и ту же продукцию.При этом1-й заводпроизводит 25%, 2-й завод − 35% и 3-й завод − 40% всей производимой продукции. Брак составляет 5% от продукции 1-го завода, 3% от продукции 2-го и 4% от продукции 3-го завода. Вся продукция смешивается и поступает в продажу. Найти: а) вероятность купить бракованное изделие; б) условную вероятность того, что купленное изделие изготовлено 1-м заводом, если это изделие бракованное. | |||||||||||||||||||||||||
| Возможно короткое замыкание, вероятность которого равна 0,0005 для каждого провода коммуникации. Всего проходит 4000 проводов. Определить вероятность возникновения обесточивания всей системы, если для этого достаточно хотя бы одного замыкания. | |||||||||||||||||||||||||
Непрерывная случайная величина Х задана функцией распределения
 .
Найти плотность распределения .
Найти плотность распределения 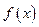 , числовые характеристики , числовые характеристики  и и  . Построить графики функций . Построить графики функций  и и 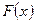 . .
| |||||||||||||||||||||||||
Ниже приводятся данные о возрастном составе безработных по Российской Федерации, зарегистрированных в службе занятости по сведениям на последнюю неделю марта 2012 г., %.
Найдите средний возраст безработных мужчин и женщин, дисперсию, среднее квадратическое отклонение и коэффициент вариации. Оцените различия показателей возрастного состава безработных мужчин и женщин. Сделайте выводы. | |||||||||||||||||||||||||
Из партии изделий объемом в 15000 штук сформирована выборка размером 150 единиц, распределение которых по значению признака X дается следующей таблицей:
Определить: а) Пределы, в которых с вероятностью 0,975 заключено среднее значение величины X; б) Вероятность того, что доля признака Y для X не менее 40, во всей совокупности, отличается от выборочной доли не более чем на 0,02 (по абсолютной величине). |
| Вариант 16 | |||||||||||||||||
| Из 10 билетов выигранными являются 2. Определить вероятности того, что среди взятых наудачу 5 билетов: а) один выигрышный; б) оба выигрышных; в) нет выигрышных. | |||||||||||||||||
| Вероятность того, что саженец ели прижился, и будет расти, равна 0,8. Посажено 400 саженцев ели. Какова вероятность того, что нормально вырастут не менее 250 деревьев? | |||||||||||||||||
Непрерывная случайная величина задана функцией плотности распределения вероятностей
 Найти коэффициент A, функцию распределения
Найти коэффициент A, функцию распределения 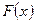 и и  , построить графики функций , построить графики функций  и и 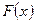 . .
| |||||||||||||||||
| По выборке 4, 6, 7, 7, 10, 15, 18 найти числовые характеристики выборки (Выборочное среднее арифметическое, выборочная дисперсия, выборочное среднее квадратическое отклонение, мода, медиана, коэффициент вариации). | |||||||||||||||||
Из партии изделий объемом в 1000 штук сформирована выборка размером 100 единиц, распределение которых по значению признака X дается следующей таблицей:
Определить: а) Пределы, в которых с вероятностью 0,925 заключено среднее значение величины X; б) Вероятность того, что доля признака Y для X не менее 54, во всей совокупности, отличается от выборочной доли не более чем на 0,01 (по абсолютной величине). |
| Вариант 17 | |||||||||||||||||||
| Из 36 карт наугад выбираются 3. Вычислите вероятность того, что среди них будут король и дама. | |||||||||||||||||||
| Вероятность того, что договор страховой компании завершится выплатой по страховому случаю, равна 0,2. Страховая компания заключила 2000 договоров. Найти вероятность того, что страховой случай наступит: а) 210 раз; б) от 180 до 300 раз включительно. | |||||||||||||||||||
Найти математическое ожидание, дисперсию и среднеквадратическое отклонение нормально распределённой случайной величины с плотностью 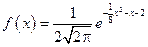 . .
| |||||||||||||||||||
По данным выборочного обследования получено следующее распределение семей по среднедушевому доходу
Постройте гистограмму распределения частот. Найдите среднедушевой доход семьи в выборке, дисперсию, среднее квадратическое отклонение, коэффициент вариации. Объясните полученные результаты. | |||||||||||||||||||
Из партии изделий объемом в 1000 штук сформирована выборка размером 100 единиц, распределение которых по значению признака X дается следующей таблицей:
Определить: а) Пределы, в которых с вероятностью 0,99 заключено среднее значение величины X; б) Вероятность того, что доля признака Y для X не менее 13, во всей совокупности, отличается от выборочной доли не более чем на 0,1 (по абсолютной величине). |
| Вариант 18 | |||||||||||||||||
| Какова вероятность того, что пятизначное число состоит из цифр 0, 1, 2, 3, 4. | |||||||||||||||||
| Вероятность рождения мальчика равна 0,51. Найти вероятность того, что среди 100 новорожденных окажется 50 мальчиков. | |||||||||||||||||
Найти математическое ожидание и дисперсию случайной величины X, заданной плотностью распределения 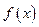 . Найдите интегральную функцию распределения, постройте графики . Найдите интегральную функцию распределения, постройте графики 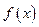 , ,  . .

| |||||||||||||||||
По данным выборочного обследования получено следующее распределение по среднедушевому доходу
Постройте гистограмму, кумуляту. Рассчитайте среднюю мощность предприятий. Найдите дисперсию. среднее квадратическое отклонение, коэффициент вариации. Сделайте анализ полученных результатов. | |||||||||||||||||
| Из партии в 5000 электрических ламп было отобрано по схеме бесповторной выборки 300. Средняя продолжительность горения ламп в выборке оказалась равной 1450 ч, а дисперсия – 40000. Какова вероятность того, что средний срок горения ламп во всей партии заключен в пределах от 1410 до 1490 ч? |
| Вариант 19 | |||||||||||||||||
| На сборку попадают детали с трех автоматов. Известно, что первый автомат дает 3% брака, второй – 2% и третий – 4%. Найти вероятность того, что на сборку попадет бракованная деталь, если с первого автомата поступает 100, со второго – 200, с третьего – 250 деталей. | |||||||||||||||||
| Вероятность появления события A в каждом из 100 независимых испытаний постоянна и равна p = 0,8. Найти вероятность того, что событие появится: а) не менее 75 раз и не более 90 раз; б) не менее 75 раз; в) не более 74 раз. | |||||||||||||||||
| Математическое ожидание распределённой по Пуассону случайной величины равно трём. Какова вероятность, что при проведении опыта значение случайной величины не превзойдёт двух? | |||||||||||||||||
По результатам выборочного обследования торговых киосков города получены следующие данные о дневной выручке частного бизнеса.
Постройте гистограмму распределения частот. Найдите среднедневную выручку от продажи товаров, дисперсию, среднее квадратическое отклонение, коэффициент вариации. Объясните полученные результаты. | |||||||||||||||||
Из генеральной совокупности извлечена выборка
Оценить с надежностью 0,95 математическое ожидание а. |
| Вариант 20 | |||||||||||||||
| На склад поступают детали заводов № 1 и № 2. Первый завод производит 80% стандартных изделий, завод № 2 – 60%. Наудачу взяли по одной детали каждого завода. Найти вероятности следующих событий: а) обе детали стандартны; б) только одна деталь стандартна; в) хотя бы одна деталь стандартна. | |||||||||||||||
Вероятность поражения мишени стрелком равна 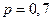 . Найти вероятность того, что при n = 2100 выстрелах мишень будет поражена ровно 1500 раз. . Найти вероятность того, что при n = 2100 выстрелах мишень будет поражена ровно 1500 раз.
| |||||||||||||||
| Известно, что в партии из 20 телефонных аппаратов 5 недействующих. Случайным образом из этой партии взято 4 аппарата. Построить закон распределения случайной величины X – числа недействующих аппаратов из числа отобранных. Найти дисперсию этой случайной величины. В каких единицах она измеряется? Построить интегральную функцию распределения случайной величины X, многоугольник распределения. | |||||||||||||||
Постройте гистограмму частот, найдите среднюю арифметическую, среднее квадратическое отклонение и коэффициент вариации для данных о дневной выручке в магазине электроники.
| |||||||||||||||
Из 2000 деталей было отобрано 400, распределение которых по размеру дается следующей таблицей:
Найти ошибку выборки при определении среднего в случаях повторного и бесповторного отбора. |
| Вариант 21 | ||||||||||||||||||||||
| На склад поступило 1500 изделий с первой фабрики и 2000 изделий со второй. Известно, что средний процент нестандартных изделий среди продукции первой фабрики равен 3%, второй – равен 2%. Найти вероятность того, что наудачу взятое со склада изделие будет нестандартным. | ||||||||||||||||||||||
Вероятность поражения мишени стрелком равна 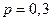 . Найти вероятность того, что при n = 2100 выстрелах мишень будет поражена от 600 до 660 раз. . Найти вероятность того, что при n = 2100 выстрелах мишень будет поражена от 600 до 660 раз.
| ||||||||||||||||||||||
Закон распределения P (X = x) приведен в таблице. Требуется: а) определить математическое ожидание M (X), дисперсию D (X) и среднее квадратическое отклонение
| ||||||||||||||||||||||
Постройте гистограмму частот, найдите среднюю заработную работников одного из цехов промышленного предприятия.
Рассчитайте среднюю арифметическую, среднее квадратическое отклонение, коэффициент вариации заработной платы. | ||||||||||||||||||||||
Для установления среднего веса изделия из 300 контейнеров организована серийная выборка с бесповторным отбором. Выбрано 6 контейнеров, каждый из которых содержит 40 изделий. Получены следующие результаты.
Найдите необходимый объем выборки, с вероятностью 0,99, гарантирующий предельную ошибку оценки среднего веса изделия в партии, равную 0,025 г. |
| Вариант 22 | |||||||||||||||||
| На склад с трех предприятий поступает продукция первого и второго сорта. В продукции первого предприятия содержится 15% второсортных изделий, в продукции второго предприятия – 25%, в продукции третьего предприятия – 30%. Чему равна вероятность того, что среди трех изделий (по одному из продукции каждого предприятия) окажутся первосортными два изделия. | |||||||||||||||||
| Вероятность поражения мишени стрелком при одном выстреле равна 0,8. Найти вероятность того, что при 100 выстрелах мишень будет поражена не менее 75 раз и не более 90 раз. | |||||||||||||||||
| Завод получает сырье на автомашинах от трех независимо работающих поставщиков. Вероятность прибытия автомашины от первого поставщика равна 0,2, от второго – 0,3, от третьего – 0,1. Составить распределение числа прибывших машин. Найти математическое ожидание и дисперсию полученной случайной величины. Построить график интегральной функции распределения. | |||||||||||||||||
Предположим, у вас есть следующая информация об акциях A и B:
Рассчитайте среднюю арифметическую, дисперсию и коэффициент вариации для акций A и B. Если вы решили купить одну акцию, какую из двух вы выберете? Почему? | |||||||||||||||||
Для определения средней урожайности пшеницы с одного гектара на площади в 20000 га проведено точное выборочное обследование, результаты которого приведены в таблице
Какова вероятность того, что средняя урожайность пшеницы на всем массиве отличается от среднего выборочного не более чем на 15 кг? |
| Вариант 23 | |||||||||||||||
| Отдел технического контроля проверяет поступающие из двух цехов изделия на стандартность. Вероятность того, что изделие цеха № 1 стандартно, равна 0,9, для изделия цеха № 2 эта вероятность равна 0,95. Найти вероятность того, что из двух проверенных изделий (по одному от каждого цеха) только одно стандартное. | |||||||||||||||
Вероятность найти белый гриб среди прочих равна  . Какова вероятность того, что: а) среди 300 грибов белых будет 75; б) белых грибов будет не менее 50 и не более 100? . Какова вероятность того, что: а) среди 300 грибов белых будет 75; б) белых грибов будет не менее 50 и не более 100?
| |||||||||||||||
Дискретная случайная величина X может принимать только два значения: 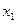 и и 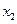 , причем , причем  . Известны вероятность . Известны вероятность  возможного значения возможного значения 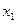 , математическое ожидание M (X) = 3,5 и дисперсия D (X) = 0,25. Найти закон распределения этой случайной величины. Отобразить найденный закон аналитически и графически. , математическое ожидание M (X) = 3,5 и дисперсия D (X) = 0,25. Найти закон распределения этой случайной величины. Отобразить найденный закон аналитически и графически.
| |||||||||||||||
Предположим, что на некотором предприятии собраны данные о числе дней, пропущенных работниками по болезни.
Постройте полигон распределения частот. Найдите среднее число пропущенных дней, стандартное отклонение, коэффициент вариации. Является ли распределение симметричным? | |||||||||||||||
| Для определения среднего процента сырого белка в зернах пшеницы было отобрано 626 зерен, обследование которых показало, что выборочное среднее равно 16,8, а выборочная дисперсия – 4. Чему равна вероятность того, что средний процент сырого белка отличается от 16,8 по абсолютной величине меньше, чем на 0,2%? |
| Вариант 24 | |||||||||||
| Среди кандидатов в студенческий совет факультета три первокурсника, 5 второкурсников и 7 третьекурсников. Из этого состава наудачу выбирают 5 человек на предстоящую конференцию. Найти вероятности следующих событий: А – будут выбраны одни третьекурсники, В – будет выбран следующий состав: 1 первокурсник, 2 второкурсника и 2 третьекурсника; С – все первокурсники попадут на конференцию; D – не будет выбрано ни одного второкурсника. | |||||||||||
| В первые классы школы должны быть приняты 200 детей. Вероятность рождения мальчика 0,515. Найти вероятность того, что среди них: а) девочек и мальчиков будет поровну; б) мальчиков меньше, чем девочек. | |||||||||||
Дано распределение дискретной случайной величины X. Построить аналитически и графически функцию распределения F (x). Найти математическое ожидание и среднее квадратическое отклонение.
| |||||||||||
| При взвешивании груза получены следующие данные 129, 125, 130, 122, 135, 125, 120, 130, 127. Определить среднее значение веса груза, среднюю ошибку взвешивания и другие показатели вариации (Выборочное среднее арифметическое, выборочная дисперсия, выборочное среднее квадратическое отклонение, мода, медиана, коэффициент вариации). | |||||||||||
| Для определения процента нестандартных изделий в партии, объем которой равен 10000, было отобрано 500 деталей, среди которых оказалось 10 нестандартных. Найти ошибку выборки при определении доли в случаях повторного и бесповторного отбора. |
| Вариант 25 | |||||||||
| Среди поступающих на склад деталей 70% из цеха 1, 30% − из цеха 2. Вероятность брака для цеха 1 равна 0,02, для цеха 2 – 0,03. Наудачу взятая деталь оказалась доброкачественной. Какова вероятность того, что она изготовлена в цехе 1? | |||||||||
| В некоторой местности из каждых 100 семей 80 имеют холодильники. Найти: 1) вероятность того, что из 400 семей 300 имеют холодильники. 2) вероятность того, что от 300 до 360 (включительно) семей из 400 имеют холодильники. | |||||||||
Дано распределение дискретной случайной величины X. Построить функцию распределения F (x), отобразить ее аналитически и графически. Найти математическое ожидание и среднее квадратическое отклонение.
| |||||||||
| При обследовании 50 членов семей рабочих и служащих установлено следующее количество членов семьи: 5; 3; 2; 1; 4; 6; 3; 7; 9; 1; 3; 2; 5; 6; 8; 2; 5; 2; 3; 6; 8; 3; 4; 4; 5; 6; 5; 4; 7; 5; 6; 4; 8; 7; 4; 5; 7; 8; 6; 5; 7; 5; 6; 6; 7; 3; 4; 6; 5; 4. Составьте вариационный ряд распределения частот. Постройте полигон распределения частот, кумуляту. Определите среднее число членов семьи. Охарактеризуйте колеблемость размера семьи с помощью показателей вариации. Объясните полученные результаты, сделайте выводы. | |||||||||
Для определения процента изделий второго сорта в партии производится случайная повторная выборка объемом 100 единиц. Определить доверительные границы для процента изделий второго сорта во всей партии, которые могут быть гарантированы с доверительной вероятностью 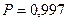 , если в выборке оказалось 25 изделий второго сорта. , если в выборке оказалось 25 изделий второго сорта.
|
| Вариант 26 | |||||||||||||
| Турист, заблудившись в лесу, вышел на полянку, от которой в разные стороны ведут 5 дорог. Если турист пойдет по первой дороге, то вероятность выхода туриста из леса в течение часа составляет 0,6; если по второй – 0,3; если по третьей – 0,2; если по четвертой – 0,1; если по пятой – 0,1. Какова вероятность того, что турист пошел по первой дороге, если через час он вышел из леса? | |||||||||||||
| В магазине 5 холодильников. Вероятность выхода из строя каждого холодильника в течение года равна 0,2. Найти вероятность того, что в течение года ремонта потребует: 1) 4 холодильника; 2) не менее 2 холодильников; 3) не более 1 холодильника; 4) не менее 1 холодильника. | |||||||||||||
| Вероятность выигрыша по лотерейному билету равна 0,2. Куплено 3 билета. Найти закон распределения и математическое ожидание случайной величины X – числа выигрышных билетов. Функцию распределения отобразить аналитически и графически. | |||||||||||||
При обследовании надоя коров случайным образом отобрали 307 коров, данные по ним сгруппировали и составили таблицу
Найти выборочное среднее, дисперсию, среднее квадратическое отклонение, моду, медиану, коэффициент вариации. | |||||||||||||
Выборочно обследовали качество кирпича. Из 1600 проб в 32 случаях кирпич оказался бракованным. Требуется определить, в каких пределах заключается доля брака для всей продукции, если результат необходимо гарантировать с вероятностью  . .
|
| Вариант 27 | ||||||||||||
У фотолюбителя в коробке находится 5 одинаковых кассет с
Дата добавления: 2017-02-11; Мы поможем в написании ваших работ!; просмотров: 2498 | Нарушение авторских прав Поиск на сайте: Лучшие изречения: |
Ген: 0.013 с.





 .
. , «исправленное» стандартное отклонение S (X) и коэффициент вариации V изучаемого признака;
, «исправленное» стандартное отклонение S (X) и коэффициент вариации V изучаемого признака;
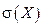 случайной величины X; б) построить график этого распределения, в) функцию распределения отобразить аналитически и графически.
случайной величины X; б) построить график этого распределения, в) функцию распределения отобразить аналитически и графически.
