Задачи для подготовки к экзамену по математике (2 семестр)
Приложения производной к исследованию функцию
1) Найти промежутки монотонности функции, точки экстремума
1)  2)
2)  3)
3)  4)
4)  5)
5)  6)
6)  7) y =ln (1-x2)
7) y =ln (1-x2)
8)  9)
9)  10)
10)  11)
11)  12)
12) 
2) Найти промежутки выпуклости-вогнутости, точки перегиба
1)  2)
2)  3)
3)  4)
4)  5)
5) 
6)  7)
7)  8)
8)  9)
9)  10)
10) 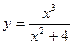
1) 11)  , 12)
, 12)  , 13)
, 13)  , 14)
, 14) 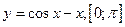 .
.
3) Найти асимптоты графиков функций
1)  2)
2)  3)
3)  4)
4)  5) y=
5) y= 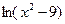 6)
6) 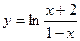 7) y=xe-x
7) y=xe-x
8)  9)
9)  10)
10)  11)
11)  12)
12) 
4). Исследовать функцию:
y=16x2(x-1)2 y=x2(x-2)2 y=2x3+3x2-5 y=(x-1)2(x-3)2 y=-(x-2)2(x-6)2/16
y=x(12-x2)/8 y=-(x2-4)2/16 y=(2x-1)2(2x-3)2
2) Найти наибольшее и наименьшее значения функции 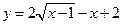 на отрезке
на отрезке  .
.
3) Найти наибольшее и наименьшее значение функции  на отрезке
на отрезке 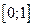 .
.
4) Найти наибольшее и наименьшее значение функции 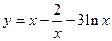 на отрезке [1;4].
на отрезке [1;4].
5) Найти наибольшее и наименьшее значение функции  на отрезке
на отрезке 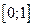 .
.
Функции нескольких переменных
1. Дана функция z=f(x,y), точка М(х,у) и вектор 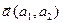 . Найти производную по направлению вектора
. Найти производную по направлению вектора  в точке М.
в точке М.
1. z=xy-2x2+4y-5; M(2,3),  (2,-1)
(2,-1)
2 z=  ; M (2, 2),
; M (2, 2),  (-3, 4)
(-3, 4)
3. z=  ; M(-1, 2),
; M(-1, 2),  (-2,1)
(-2,1)
4. z=  ; M(2, 1),
; M(2, 1),  (4,-3)
(4,-3)
5. z= 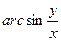 ; M(4,3),
; M(4,3),  (-2,3)
(-2,3)
2. Найти наибольшее и наименьшее значение функции в замкнутой области Д.
1. z=x2-2x+y2-2у+2; Д: 
2. z=x3+y3-3ху; Д: 
3. z=x2у(4-x-у); Д: 
4. z=x2+2xу-4х+3у; Д: 
5. z=x3 +y3+3ху; Д: 
1) Дана функция  . Доказать, что
. Доказать, что  .
.
2) Дана функция  . Доказать, что
. Доказать, что  .
.
3) Дана функция  , точка
, точка  и вектор
и вектор  . Найдите производную в точке
. Найдите производную в точке  по направлению вектора
по направлению вектора  .
.
4) Дана функция  . Доказать, что
. Доказать, что  .
.
5) Найти наибольшее и наименьшее значение функции  в замкнутой области
в замкнутой области  .
.
6) Найти экстремумы функции 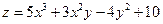 .
.
7) Найти наибольшее и наименьшее значения функции  в замкнутой области
в замкнутой области  .
.
8) Найти экстремумы функции  .
.
9) Дана функция  , точка
, точка  и вектор
и вектор  . Найдите производную в точке
. Найдите производную в точке  по направлению вектора
по направлению вектора  .
.
10) Дана функция  . Доказать, что
. Доказать, что  .
.
Неопределенные и определенные интегралы
А. Метод подведения под знак дифференциала










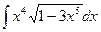

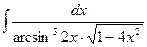











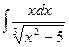


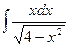
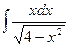


 .
.









Б. Метод интегрирования по частям
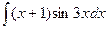


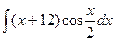













 (x+12)cos
(x+12)cos 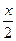 dx
dx 

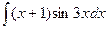
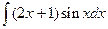 .
.
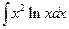







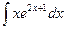 .
.
В. Метод неопределенных коэффициентов








Г. Метод замены переменной
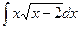




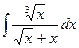

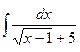



 .
. 


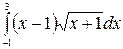



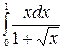





Приложения определенного интеграла
а) найти площадь фигуры, ограниченной линиями (в полярной системе координат)
1) вне кардиоиды 2) вне окружности
r=1,5; r=1+cosφ r=1; r=1-sinφ r=2; r=2(1+sinφ) r=cos2φ
r=0,5; r=1-cosφ; r=cosφ; r=1-cosφ r=3sinφ; r=1+sinφ r =2(1-sin 
r=1; r=2sin2φ r=cos2φ r=  ; r=2cos2φ r=
; r=2cos2φ r=  ; r=2sin2φ
; r=2sin2φ
r =3cos2  r =1; r=1-sinφ
r =1; r=1-sinφ
б) в декартовой системе координат
y=4x2, 9 y=x2, y=2 xy=4, y=4x, 4y=x, x>0,y>0 9x=5y2, x=y2-4
x=2y-y2, y=lnx, y=2, y=0 y=2x, y=2x-x2, x=0, x=2 xy=1, y=2x, 2y=x, x>0, y>0
y=x2+x-2, x+y=1 y=ex, y=lnx, x+y=1, x=3 y=cosx, y=-x+3, x=0, y=0
 ;
;  ,x=-2 y=ex, y=lnx, x+y=1, x=3
,x=-2 y=ex, y=lnx, x+y=1, x=3
y=2x, y=2x-x2, x=0, x=2 y=sinx, y=1, x=0 y=x2+x-2, x+y=1
 , x=8, y=0 y=4x2, 9 y=x2, y=2
, x=8, y=0 y=4x2, 9 y=x2, y=2
Y=x2-1; 2x-y+2=0 Y=-x2-2x+3; y=3-4x
Y=x2-3x+2; y=x+2 Y=5-x2; x-y+3=0
Y=x2-6x+5; y=2x-7 Y=x2+x-2; x+y=1
Y=-x2-6x+5; y=2x-4 Y=3x2+1; y=3x+7
Y=9-x2; y=x+3 Y=x2; y=x+2
y = x  -2x+1, 2x-y-2=0. y = x
-2x+1, 2x-y-2=0. y = x  -3x+1, x-y-1=0.
-3x+1, x-y-1=0.
y = x  -3x, x-y-3=0. y = x
-3x, x-y-3=0. y = x  -5x+4, x+y-1=0.
-5x+4, x+y-1=0.
y = x  -2x-3, 2x-y-6=0. y = x
-2x-3, 2x-y-6=0. y = x  -x-2, 3x-y-5=0.
-x-2, 3x-y-5=0.
y = x  -6x+5, 2x+y-2=0. y = x
-6x+5, 2x+y-2=0. y = x  -6x+8, 2x+y-5=0.
-6x+8, 2x+y-5=0.
y = x  -2x, 2x-y-3=0. y = x
-2x, 2x-y-3=0. y = x  -5x+6, x+y-3=0.
-5x+6, x+y-3=0.
б) найти объем тела вращения
y2=(x-1)3, x=2 OX; xy=-2, x=1, x=2 y=0 OX; xy=1, y=x2, y=2, x=0 OY;
y=x2, y=2-x2 OY; xy=6, x+y-7=0 OX; y2=(x+4)3, x=0 OY; y2=(x+4)3 OX;
Найти обьем тела вращения вокруг оси Ох:
y=4+x  , y=4+x, x>0 y=x
, y=4+x, x>0 y=x 
y=  xy=-2, x=1, x=2 y=0 y2=(x-1)3, x=2.
xy=-2, x=1, x=2 y=0 y2=(x-1)3, x=2.
Задание5. Изменить порядок интегрирования в двойном интеграле. Сделать чертеж области интегрирования.
1.  2.
2.  3.
3.  4.
4. 
5.  6.
6. 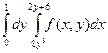 7.
7.  8.
8. 
9.  10.
10.  11.
11. 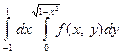 12.
12. 
13.  14.
14.  15.
15.  16.
16. 
Задание 6. Вычислить интегралы.
1.  2.
2.  3.
3.  4.
4. 
5.  6.
6. 
7.  8.
8. 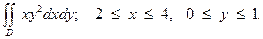
9.  10.
10. 
11.  12.
12. 
13.  14.
14. 
15.  16.
16. 
17.  18.
18. 
19.  .
.
Задание7. С помощью двойного интеграла вычислить площадь фигур, ограниченных заданными линиями:
1. 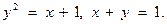 2.
2.  3.
3. 
4.  5.
5. 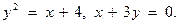 6.
6. 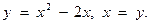
7. 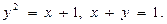 8.
8.  9.
9. 
10.  11.
11.  . 12.
. 12.  .
.
13.  . 14.
. 14.  15.
15.  .
.
Задание 8. Дифференциальные уравнения первого порядка
А. Уравнения с разделяющимися переменными
1.  2.
2.  3. ylnydx+xdx=0 4. y’ctgx+y=2
3. ylnydx+xdx=0 4. y’ctgx+y=2
5.  6.
6.  7.
7. 
Б. Линейные уравнения
y/sinx-y cosx =1, y/-y sinx=e-cosxsin2x y/cosx - 2y sinx=2 y/x lnx – y=3x3ln2x, 



















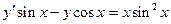


 .
.
Найти решение задачи Коши:
xy|-3y=x4ex y0=e x0=1 




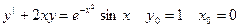



Б. Уравнения Бернулли

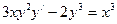

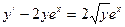


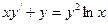
Г. однородные уравнения
(x-y)dx+xdy=0; x2dy=(y2-xy+x2)dx; 2x2y/=x2+y2;  ; xy/=y(lny - lnx)
; xy/=y(lny - lnx)


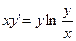

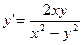
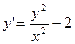


 .
.
 .
. 



Дифференциальные уравнения второго порядка
А. Линейные дифференциальные уравнения второго порядка со специальной правой частью


 .
. 
 .
. 
 .
. 
 .
. 


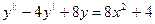
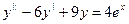






y”+y’-2y = 8  -4x y”-3y’ = 18
-4x y”-3y’ = 18  -2 y”+2y’+y = 4
-2 y”+2y’+y = 4  -3x-5
-3x-5
y”-4y’+3y = 8 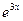 y”-2y’-2y =12x
y”-2y’-2y =12x 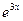 y”-2y’+y = 10
y”-2y’+y = 10 
y”+y = cos3x y”+4y = cos2x y”+5y’+6y = -50sin4x.
y”-2y’+2y =  sinx
sinx
Найти решение задачи Коши:
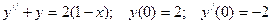



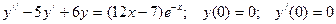
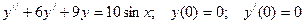


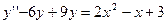


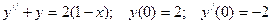





в) метод вариации произвольной постоянной













