КОНТРОЛЬНАЯ РАБОТА № 1
Таблица вариантов для контрольной работы № 1
| Вариант | Номера задач | |||||
1. ОСНОВНЫЕ ФОРМУЛЫ, НЕОБХОДИМЫЕ ДЛЯ РЕШЕНИЯ
1. Скорость движения материальной точки
 ,
,
где 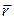 – радиус–вектор, x, y, z – координаты точки,
– радиус–вектор, x, y, z – координаты точки, 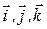 - единичные векторы.
- единичные векторы.
Модуль мгновенной скорости
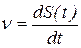 ,
,
где S(t) – зависимость пути, пройденного точкой от времени.
2. Ускорение движения материальной точки
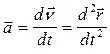 .
.
Нормальная и тангенциальная составляющие ускорения
 .
.
Модуль ускорения
 .
.
3. Путь, пройденный материальной точкой с момента времени t1 до момента t2
 .
.
4. Угловая скорость и угловое ускорение вращательного движения твердого тела
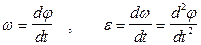 .
.
5. Связь между линейными и угловыми величинами при вращении тела
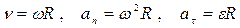 .
.
6. Основное уравнение динамики материальной точки и поступательного движения твердого тела
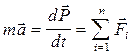 ,
,
где 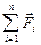 – равнодействующая всех сил, приложенных к телу,
– равнодействующая всех сил, приложенных к телу, 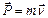 – импульс.
– импульс.
7.
Работа и мощность переменной силы

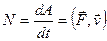 .
.
8. Связь между потенциальной энергией частицы и силой со стороны поля
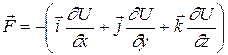 .
.
9. Основное уравнение динамики вращательного движения твердого тела
 ,
,
где J – момент инерции тела, L = Jw – момент импульса, M – момент внешних сил.
10. Момент инерции твердого тела
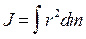 .
.
Момент инерции тел правильной геометрической формы относительно неподвижной оси вращения
| Форма тела | Ось вращения | Момент инерции |
| 1.Однородный шар радиусом R и массой m | Проходит через центр масс | 0.4mR2 |
| 2.Однородный сплошной цилиндр или диск радиусом R и массой m | Проходит через центр масс перпендикулярно плоскости основания | 0.5mR2 |
| 3. Тонкий обруч или кольцо радиусом R и массой m | Проходит через центр масс перпендикулярно плоскости обруча | mR2 |
| 4. Однородный тонкий стержень длиной L и массой m | Проходит через центр масс перпендикулярно стержню | mL2/12 |
| 5. Однородный тонкий стержень длиной L и массой m | Проходит перпендикулярно стержню через его конец | mL2/3 |
Теорема Штейнера
 ,
,
где J – момент инерции тела массой m относительно произвольной оси;
J0– момент инерции тела относительно оси, проходящей через центр инерции тела параллельно заданной оси; a – расстояние между осями.
11. Модуль момента силы
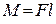 ,
,
где  - кратчайшее расстояние между линией действия силы и осью вращения.
- кратчайшее расстояние между линией действия силы и осью вращения.
12. Кинетическая энергия и работа внешних сил при вращении твердого тела вокруг неподвижной оси
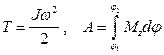
13. Кинетическая энергия тела, катящегося по плоскости без скольжения
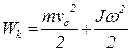 ,
,
где m – масса тела, vc – скорость центра масс тела, J– момент инерции тела относительно оси, проходящей через центр масс, w - угловая скорость вращения тела.
14.Аналогия между формулами поступательного и вращательного движения.
| Поступательное движение | Вращательное движение |
| 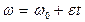
|
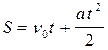
| 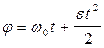
|
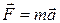
| 
|
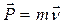
| 
|
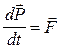
| 
|

| 
|

| 
|
15.Условия равновесия тела: векторные суммы всех сил и моментов сил, действующих на тело равны нулю 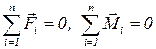 .
.
16.Гидростатическое давление столба жидкости высотой h: 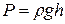 ,
,
где r - плотность жидкости.
17.Уравнение Бернулли для ламинарного течения идеальной жидкости
 ,
,
где P – статическое давление жидкости в заданном сечении трубы, V – скорость жидкости в этом сечении.
18.Сила сопротивления среды с вязкостью h шару радиуса r движущемуся со скоростью V
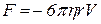 .
.
19.Релятивистское замедление хода часов:
 ,
,
t - промежуток времени между событиями, отсчитанное покоящимися часами;  - промежуток времени между событиями, отсчитанное часами, движущимися вместе с телом со скоростью v, с – скорость света.
- промежуток времени между событиями, отсчитанное часами, движущимися вместе с телом со скоростью v, с – скорость света.
20. Релятивистское сокращение длины:
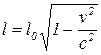 ,
,
где l0 - собственная длина тела в покоящейся системе координат, l - длина тела, измеренная в направлении движения в системе отсчёта, относительно которой он движется со скоростью v.
21. Масса релятивистской частицы, имеющей массу покоя m0:
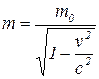 .
.
22. Энергия покоя частицы:
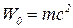 .
.
23. Полная энергия частицы:
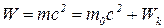 .
.
24. Кинетическая энергия частицы:
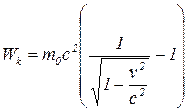 .
.
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача 1. Кинематическое уравнение движения материальной точки по прямой (ось х) имеет вид х = А + В t + С t3, где А = 4 м, В = 2 м/с, С = - 0,5 м/с2. Для момента времени t1 = 2 с определить: 1) координату х1 точки; 2) мгновенную скорость V1; 3) мгновенное ускорение а1.
Решение. Найдем координату точки, для которой известно кинематическое уравнение движения, подставив в уравнение движения вместо t заданное значение t1:
х1 = А + В t1 + С t13; х1 = 4 м.
Мгновенную скорость V в произвольный момент времени t найдем, продифференцировав координату х по времени:
V = dx/dt = B + 3Ct2.
Тогда в заданный момент времени мгновенная скорость:
V1 = B + 3Ct21; V1 = - 4 м/с.
Знак минус указывает на то, что в момент времени t1 = 2 с точка движется в отрицательном направлении координатной оси.
Мгновенное ускорение в произвольный момент времени найдем, взяв вторую производную от координаты по времени:
a = d2x/dt2 = 6Ct.
Мгновенное ускорение в заданный момент времени равно: a1 = 6Ct1; a1 = - 6 м/c2.
Знак минус указывает на то, что направление вектора ускорения совпадает с отрицательным направлением координатной оси.
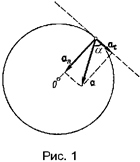
Задача 2. Тело вращается вокруг неподвижной оси по закону, выражаемому формулой φ = 10 + 20 t - 2 t2 (рис. 1). Найдите по величине и направлению полное ускорение точки, находящейся на расстоянии R = 0,1 м от оси вращения, для момента времени t1 = 4 с.
 Условие:
Условие:
φ=10+20t-2t2;
R=0,1 м;
t1=4 c;
a -? α -?
Решение. Точка вращающегося тела описывает окружность. Полное ускорение точки определяется геометрической суммой тангенциального и нормального ускорения:
a = (a2t + a2n)1/2. (1)
Тангенциальное и нормальное ускорения точки вращающегося тела выражаются формулами:
а t = εR; (2)
an = ω2R, (3)
где ω - угловая скорость тела; ε - его угловое ускорение; R - расстояние от оси вращения.
Подставляя выражения аt и аn в формулу (1) находим:
a = R(ε2 + ω4)1/2. (4)
Угловая скорость вращающегося тела равна первой производной от угла поворота по времени
ω = dφ/dt = 20 – 4t.
В момент времени t = 4 с угловая скорость ω = 4 с-1.
Угловое ускорение вращающегося тела равно первой производной от угловой скорости по времени: ε = dω/dt = - 4 c-2.
Подставляя найденные и заданное значения в формулу (4) получим: a = 1,65 м/c2.
Направление полного ускорения можно определить, если найти углы, которые векторы ускорения составляют с касательной к траектории или нормалью к ней:
cos α = at/a. (5)
По формулам (2) и (3) найдем значения аt и an:
at = - 0,4 /c2; an = 1,6 /c2.
Подставив эти значения и значения полного ускорения в формулу (5), получим:
cos α = 0,242; α = 760.
Задача 3. На горизонтальной платформе шахтной клети стоит человек массой m = 60 кг. Определить силу давления человека на платформу: 1) при ее подъеме с ускорением
а1 = 3 м/с2; 2) при равномерном подъеме и спуске; 3) при спуске с ускорением а3 = 9,8 м/с2.
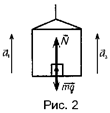 Условие:
Условие:
m=60 кг;
а1=3 м/с2;
v2=const, a2=0;
а3=9,8 м/с;
F1-? F2 -? F3 -?
Решение. На человека, стоящего на платформе шахтной клети действуют две силы: сила тяжести m g и сила реакции опоры N. Согласно второму закону Ньютона:
m a = m g + N (6)
Согласно третьему закону Ньютона сила давления человека на платформу равна силе реакции опоры:
N = - F N = F (7)
1. Согласно рис. 2 запишем уравнение (6) в проекции на ось У
ma1 = N1 – mg
Учитывая (7) в (8) получим
F1 = N1 = m (g + a1), F1 = 783 H.
2. При равномерном движении шахтной клети а2 = 0 и, следовательно, сила давления человeка на платформу равна силе тяжести: F2 = N2 = mg.
3. При спуске платформы с ускорением, направленным вниз уравнение движения платформы имеет вид ma3 = mg – N3.
Откуда сила давления человека на платформу: F3 = N3 = =m(g – a3).
Учитывая, что а3 = g имеем F3 = 0. Следоватeльно, человек не давит на платформу.
Задача 4. Каким был бы период обращения ИСЗ на круговой орбите, если бы он был удален от поверхности Земли на расстояние, равное земному радиусу (R = 6400 км).
Условие: h = R = 6370 км;
Т -?
Решение. Период обращения ИСЗ по круговой орбите
Т = 2π(R + h)/V = 4πR/V.
Для определения скорости спутника учтем, что при его движении по круговой орбите на спутник действует только сила притяжения Земли Ft, сообщающая ему нормальное ускорение:
Ft = Fn; GmM/(R+h)2 = mV2/(R+h),
где G – гравитационная постоянная, m – масса спутника, M – масса Земли.
Отсюда скорость спутника равна
V = (GM/(R + h)1/2 = (GM/2R)1/2.
Учитывая, что
GmM/R2 = mg,
где g – ускорение силы тяжести на поверхности Земли, получаем
V = (gR/2)1/2.
Подставляя это значение скорости в формулу периода, найдем, что
Т = 4 (2R/g)1/2 = 14360 c = 3 ч 59 мин.
Задача 5. Стальная прoвoлока сечением S= 3 мм2 под действием растягивающей силы, равной F = 4 . 104 Н имеет длинy L1 = 2 м. Определить абсолютное удлинение проволоки при увеличении растягивающей силы на F1 = 104 Н. Модуль Юнга стали Е =2 . 1011 Па.
Условие:
Е = 2·1011 Па;
S= 3 мм2 =3·10-6 м2;
L1 = 2 м;
F = 4·104 Н;
F1 =1,0·104 Н;
ΔL2 -?
Решение. Для того чтобы найти абсолютное удлинение проволоки при увеличенной растягивающей силе, необходимо узнать ее первоначальную длину L. Из закона Гука
F = εE = E(L1 – L)S/L
находим L = EL1S/(F +ES).
При увеличении растягивающей силы на величину F1
F + F1 = EΔL2S/L.
Откуда ΔL2 = (F + F1)L/ES.
Заменив L выражением, записанным выше, получаем
ΔL2 = (F + F1)L1/(F + ES).
Подставив данные, находим: ΔL2 = 0, 16 м.
Задача 6. Маховик, массу которого m = 5 кг можно считать распределенной по ободу радиуса r = 20 см, свободно вращается вокруг горизонтальной оси, проходящей через его центр с частотой n = 720 мин-1. При торможении маховик останавливается через Δt = 20 с. Найти тормозящий момент М и число оборотов N, которое сделает маховик до полной остановки.
Условие:
m = 5 кг
r = 20см =0,20 м
n =720 мин-1 = 12 с-1
Δt =20 с
М -? N -?
Решение. Если тормозящий момент постоянен, то движение маховика равнозамедленное, и основное уравнение динамики вращательного движения можно записать в виде:
J∆ ω = M ∆t, (9)
где ∆ ω = ω – ω0 - изменение угловой скорости за интервал времени ∆t; М – искомый тормозящий момент.
Число оборотов N может быть найдено как кинематически, так и по изменению кинетической энергии, равному работе совершаемой тормозящей силой.
Векторному уравнению (9) соответствует скалярное уравнение
J∆ω = M∆t, (10)
где ∆ω, M - модули соответствующих векторов.
Из условия задачи следует, что
∆ω = |ω – ω0 | = ω0 =2πn (11)
Поскольку масса маховика распределена по ободу, момент инерции
J = mr2 (12)
Подставляя выражения (11), (12) в (10) получим
mr22πn = M∆t.
Откуда M = 2πnmr2/Δt = 0,75 Hм.
Векторы M, Δ ω направлены в сторону противоположную вектору ω0.
Угловое перемещение, пройденное маховиком до остановки
φ = ω0∆t – ε∆t2/2. (13)
Учитывая, что ω = ωo - ε∆t = 0 преобразуем выражение (13)
φ = ω0∆t/2.
Так как φ = 2πN, ω =2πn,
где N - число оборотов, которое делает маховик до полной остановки, окончательно получим
N = nt/2 = 120 об.
Задача 7. На скамье Жуковского сидит человек и держит в вытянутых руках гири массой m =10 кг каждая. Расстояние от каждой гири до оси вращения скамьи l 1 = 50 см. Скамья вращается с частотой n1 = 1,0 с-1. Как изменится частота вращения скамьи и какую работу A произведет человек, если он сожмет руки так, что расстояние от каждой гири до оси уменьшится до l 2 = 20 см. Суммарный момент инерции человека и скамьи относительно оси вращения J =2,5 кг·м2. Ось вращения проходит через центр масс человека и скамьи.
Условие:
m = 10 кг;
l 1=50 см = 0,5 м;
n1 =1,0 с-1;
l 2 =20 см =0,2 м;
J = 2,5 кг·м2.
n2 -? А -?
Решение. Частота вращения скамьи Жуковского изменится в результате действий, производимых человеком при сближении гирь. В системе тел скамья – человек – гири все силы, кроме сил реакции опоры, являются внутренними и не изменяют момента импульса системы. Однако моменты сил реакции опоры относительно вертикальной оси равны нулю. (Для скамьи Жуковского силы трения в оси можно считать отсутствующими.) Следовательно, момент импульса этой системы остается постоянным:
L1 = L2; J1 ω1 = J2 ω2, (14)
где J1 ω 1, J2 ω 2 - моменты импульса системы соответственно до и после сближения гирь.
Перепишем векторное уравнение (14) в скалярном виде:
J1ω1 = J2ω2. (15)
До сближения гирь момент инерции всей системы
J1 = J0 + 2m l 12.
После сближения
J2 = J0 + 2m l 22,
где m - масса каждой гири.
Выражая угловую скорость через частоту вращения по формуле ω = 2πn и подставляя ее в уравнение (15) получаем
(J0 + 2m l 12)n1 = (J0 + 2m l 22)n2.
Откуда
n2 = n1(J0 + 2ml12)/(J0 + 2ml22) = 2,3 c-1.
Все внешние силы не создают вращающего момента относительно оси и, следовательно, не совершают работы. Поэтому изменение кинетической энергии системы равно работе, совершенной человеком:
A = W2 - W1 = J2ω22 /2– J1ω12/2.
Учитывая, что ω2 = J1ω1/J2, получаем работу, совершаемую человеком:
A = J1(J1 – J2)ω12/2J2 = (J0 + 2m l 12) 2π2 n12(l 12 – l 22)/(J0 + 2m l 22) = 190 Дж.
Задача 8. Автомобиль массой m = 2000 кг движется вверх по наклонной плоскости с уклоном α = 0,1, развивая на пути S = 100 м скорость vк = 36 км/ч. Коэффициент трения μ = 0,05. Найти среднюю и максимальную мощность двигателя автомобиля при разгоне.
Условие:
m =2000 кг;
 S=100 м;
S=100 м;
a=0,1 м/с2;
μ=0,05;
v0 =0;
vк =36км/ч = 10м/с;
Рср -? Рmax -?
Решение. Автомобиль движется равноускоренно, причем начальная скорость равна нулю. Выберем ось х, расположенную вдоль наклонной плоскости, ось у – перпендикулярно ей (рис. 3).
На автомобиль действует четыре силы: сила тяжести FТ =m g, сила реакции опоры N, сила тяги F и сила трения FТР. Запишем основной закон динамики:
m a = N + m g + F + FTP.
Это уравнение в проекциях на оси координат
на ось х ma = F – mg sina - FTP,
на ось у 0 = N – mg cosa,
FTP = μ N.
Выразим из этих уравнений силу тяги F
F = mg sina + μmg cosa + ma.
Ускорение
a = (vk 2 - v02)/(2s) = vk2/(2s).
Найдем работу двигателя на этом участке:
A = Fs cos α,
где α – угол между F и s, равный нулю.
Подставив сюда выражение для F, получим
A = [mg sinα + μmg cosα + mvk2/(2s)]s.
Средняя мощность равна PCP = A/t, где t = (vk – v0)/a = 2s/vk2, откуда
PCP = m[g sin α + μg cos α + vk2/(2s)]·(vk/2).
Максимальная мощность автомобиля достигается в тот момент, когда скорость максимальна:
Pmax = F·vk,
Pср = 27·104 Вт, Pmax = 47·104 Вт.
Задача 9. Деревянный стержень массой М=6,0 кг и длиной l=2,0 м может вращаться в вертикальной плоскости относительно горизонтальной оси, проходящей через точку О (рис. 4). В конец стержня попадает пуля массой m = 10 г, летящая со скоростью V0 =1,0·103 м/с, направленной перпендикулярно стержню и застревает в нем. Определить кинетическую энергию стержня после удара.
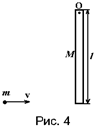 Условие:
Условие:
М = 6,0 кг;
l = 2,0 м;
m = 10 г = 1,0·10–2;
v0 = 1,0 . 103 м/с;
Wк -?
Решение. Физическая система образована из двух тел: стержня и пули. Пулю можно считать за материальную точку, стержень примем за твердое тело. Пуля до взаимодействия двигалась прямолинейно, а после взаимодействия вместе со стержнем вращается вокруг неподвижной оси. Применим закон сохранения момента импульса относительно этой оси. Условия применимости этого закона – замкнутость системы выполнены.
По закону сохранения момента импульса:
L1 =L2 (16),
где L1 =mv0l – момент импульса пули относительно оси вращения до удара;
L2 = Jω – момент инерции стержня и пуль относительно оси вращения;
J = J1 + J2,
где J1 = Ml2/3 – момент инерции стержня; J2 = ml2 – момент инерции пули.
Учитывая вышеизложенное в (16), получим
mv0l = (M/3 + m)l2ω
Так как m << M, можно приближенно считать, что
mV0l = Ml2ω /3,
откуда ω = 3mv0/Ml.
Кинетическая энергия стержня
Wк = Jω2/2 = 3 m2V20/2M = 25 Дж.
Задача 10. Определить релятивистский импульс р и кинетическую энергию электрона, движущегося со скоростью V=0,9 с (где с – скорость света в вакууме).
Условие:
V = 0,9 c;
m0 = 9,1·10-31 кг;
р -? Wк -?
Решение. Релятивистский импульс р = m0V/ (1 – V2/c2)1/2 = =5,6·10-22 кг·м/с.
В релятивистской механике кинетическая энергия определяется как разность между полной энергией W и энергией покоя W0
Wк = W – W0 = mc2 – m0c2 = (m – m0)c2
Получим
Wк = m0c2  = 0,66 МэВ.
= 0,66 МэВ.
Q23 = i (p2 V2 – p V2) = - 1050 Дж.
ЗАДАЧИ
100. Камень бросили с крутого берега реки вверх под углом 30° к горизонту со скоростью v0=10 м/с. С какой скоростью он упал в воду, если время полета t=2,5 с?
101. Кинематические уравнения движения двух материальных точек имеют вид x1 = A1 + B1t2 + C1t3 и x2 = A2 + B2t2 + C2t3, где B1 = 4 м/с2; C1 = - 3 м/с3; B2 = - 2 м/с2; С2 = 1 м/с3. Определить момент времени, для которого ускорения этих точек будут равны.
102. Движение материальной точки задано уравнениями: х = 8 t2 + 4, (м); y = 6 t2 – 3, (м); z = 0. Определить модули скорости и ускорение точки в момент времени t = 10 с. Изобразите на рисунке их направления.
103.Точка движется по прямой согласно уравнению
x = At + Bt3,
где А=6 м/с, В=0,125 м/с3. Определить среднюю скорость точки в интервале времени от  = 2 с до
= 2 с до  = 6 с.
= 6 с.
104. Мяч брошен со скоростью V0 = 10 м/с под углом a=600 к горизонту. Определите радиус кривизны R траектории мяча в верхней точке траектории и в момент его падения на землю.
105. Найти, во сколько раз нормальное ускорение точки, лежащей на ободе вращающегося колеса, больше ее тангенциального ускорения для того момента, когда вектор полного ускорения этой точки составляет угол 30° с вектором ее линейной скорости.
106. Ротор электродвигателя, имеющий частоту вращения n = 955 об/мин, после выключения остановился через t = 10 с. Считая вращение равнозамедленным, определить угловое ускорение ротора после выключения электродвигателя. Сколько оборотов сделал ротор до остановки?
107. Вентилятор вращается с частотой n=600 об./мин. После выключения вентилятор, вращаясь равнозамедленно, сделал до остановки N = 125 оборотов. Какое время t прошло с момента выключения вентилятора до его полной остановки?
108. Твердое тело начинает вращаться вокруг неподвижной оси с угловым ускорением e = Вt3, где В = 0,02 рад/с3. Через сколько времени после начала вращения вектор полного ускорения произвольной точки тела будет составлять угол 60° с ее вектором скорости?
109. Твердое тело вращается вокруг неподвижной оси по закону j = Аt – Вt3, где А = 6,0 рад/с, В = 2,0 рад/с3. Найти средние значения угловой скорости и углового ускорения за промежуток времени от начала движения до остановки. Определить угловое ускорение в момент остановки тела.
110. Катер массой m = 2т с двигателем мощностью N = 80 кВт развивает максимальную скорость v = 24 м/с. Определить время, в течение которого катер после выключения двигателя потеряет половину своей скорости. Принять, что сила сопротивления движению катера изменяется пропорционально квадрату скорости.
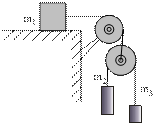
111. В системе, показанной на рисунке массы тел равны m1=1,5 кг, m1=2,5 кг, m2=1,5 кг, трения нет, массы блоков пренебрежимо малы. Найти ускорение тела m1.
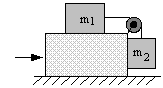
112. С каким минимальным ускорением следует перемещать в горизонтальном направлении брусок, чтобы тела 1 и 2 не двигались относительно него? Массы тел m1=2 кг и m2=1 кг, коэффициент трения между бруском и обоими телами k =0,05. Массой блока пренебречь.
113. Если к телу приложить силу F = 120 Н под углом a=60о к горизонту, то тело будет двигаться равномерно. С каким ускорением а будет двигаться тело, если ту же силу приложить под углом b=30о к горизонту? Масса тела m = 25 кг.
114. На концах нити, перекинутой через неподвижный блок, подвешены два тела массой m = 240 г каждое. С какой массой mД надо положить добавочный груз на одно из тел, чтобы каждое из них прошло за t = 4 c путь S = 160 cм?
115. Из ствола автоматического пистолета вылетела пуля массой m1=10 г со скоростью v1=300 м/с. Затвор пистолета массой m2=200 г прижимается к стволу пружиной, жесткость которой k=25 кН/м. На какое расстояние отойдет затвор после выстрела? (Считать, что пистолет жестко закреплен.)
116. На покоящийся шар налетает со скоростью v=4м/с другой шар одинаковой с ним массы. В результате столкновения шар изменил направление движения на угол 30°. Определить скорости шаров после удара. Удар считать абсолютно упругим.
117. Снаряд, летевший горизонтально со скоростью V =100 м/с, разрывается на две равные части на высоте H =40 м. Одна часть падает через t = 1 с на землю под местом взрыва. Определить величину V2 и направление скорости второй части сразу после взрыва.
118. Конькобежец массой М =60 кг, стоя на коньках на льду, бросает в горизонтальном направлении мяч массой m = 1 кг со скоростью V = 10 м/с. На какое расстояние откатится при этом конькобежец, если коэффициент трения коньков о лед m=0,01?
119. Какова средняя сила давления <F> на плечо при стрельбе из автомата, если масса пули m = 10 г. а скорость пули при вылете из канала ствола V= 300 м/с. Автомат делает N = 300 выстрелов в минуту.
120. Тело массой 990 г лежит на горизонтальной поверхности. В него попадает пуля массой 10 г и застревает в нем. Скорость пули 700 м/с и направлена горизонтально. Какой путь пройдет тело до остановки? Коэффициент трения между телом и поверхностью 0.05.
121. Определить мощность двигателя автомобиля-самосвала массой m = 40 т при его движении со скоростью v =27 км/ч, если коэффициент сопротивления движению равен μ = 0,1.
122. Из колодца глубиной h = 5 м равномерно поднимают ведро с водой массой m1 = 10 кг на веревке, каждый метр которой имеет массу m2 = 0,20 кг. Какая работа A совершается при этом?
123. Два шара подвешены на параллельных нитях одинаковой длины так, что они соприкасаются. Масса первого шара 0,2 кг, масса второго – 0,1 кг. Первый шар отклоняют так, что его центр тяжести поднимается на высоту 4,5 см, и отпускают. На какую высоту поднимутся шары после соударения, если: а) удар упругий, б) удар неупругий?
124. Тело массой m = 1,0 кг падает с высоты h=20 м. Пренебрегая сопротивлением воздуха, найти среднюю по времени мощность, развиваемую силой тяжести на пути h, и мгновенную мощность на высоте 10м.
125. Сваю массой m1 = 100 кг забивают в грунт копром, масса которого m2 = 400 кг. Копер свободно падает с высоты H =5 м и при каждом ударе свая опускается на глубину h = 5 см. Определить среднюю силу F сопротивления грунта.
126. Подъемный кран поднял груз массой 4,5.103 кг на высоту 8 м. Мощность двигателя при кране 8,832 кВт. Сколько времени затрачено на подъем груза?
127. На гладкой горизонтальной поверхности лежат два тела, между которыми находится сжатая пружина, массой которой можно пренебречь. Пружине дали возможность распрямиться, вследствие чего тела приобрели некоторые скорости v1 и v2. Вычислите их, если массы тел m1 = 1 кг, m2 = 3 кг, а энергия сжатой пружины W = 3 Дж.
128. Вагон массы 50 т движется со скоростью 12 км/ч и встречает стоящую на пути платформу массы 30 т. Найти скорость совместного движения вагона и платформы непосредственно после того, как сработала автосцепка. Вычислить расстояние, пройденное вагоном и платформой после сцепления, если сила сопротивления составляет 5% от веса.
129. Из пушки массой М= 2540 кг, находящейся у подножья наклонной плоскости, вылетает в горизонтальном направлении снаряд массы m= 12 кг. с начальной скоростью v0=800 м/с. На какую высоту поднимется пушка по наклонной плоскости в результате отдачи, если угол наклона плоскости равен a=50, а коэффициент трения пушки о плоскость равен k = 0,12?
130. Мощность излучения Солнца равна Р = 3,75·1026 Вт. На сколько уменьшается масса Солнца за один год?
131. Во сколько раз уменьшится плотность тела при его движении со скоростью 0,8 с?
132. С какой скоростью v должен двигаться в ускорителе протон, чтобы увеличение его массы не превышало k = 5%?
133. Каков возраст космонавта по часам Земли, если он в 30-летнем возрасте улетел на расстояние до 20 св. лет. Считать его возраст по часам космонавта 35 лет.
134. Релятивистская масса движущегося тела в 100 раз больше его массы покоя. Найдите скорость движения.
135. Вычислить момент инерции однородного сплошного конуса относительно его оси симметрии, если масса конуса m = 0,5 кг, а радиус его основания R= 5 см.
136. Маховик, представляющий собой диск массой m = 10 кг и радиусом r = 10 см, свободно вращается вокруг оси, которая проходит через его центр, с частотой ν = 6 с-1. При торможении маховик останавливается через t = 5 с. Определить тормозящий момент M.
137. В системе известны массы тел m1= 1 кг и m2=1,5 кг, коэффициент трения k=0,2 между телом m1 и горизонтальной плоскостью, а также масса блока m = 0,5 кг, который можно считать однородным диском.
Найти ускорение тела m2 и работу силы трения, действующей на тело m1, за первые 5 секунд после начала движения.

138. Маховик. момент инерции которого J = 63,6 кг.м2, вращается с угловой скоростью  = 31,4 рад/с. Найти момент сил торможения М под действием которого маховик останавливается через время t = 20 с. Маховик считать однородным диском.
= 31,4 рад/с. Найти момент сил торможения М под действием которого маховик останавливается через время t = 20 с. Маховик считать однородным диском.
139. На барабан радиусом R = 20 см, момент инерции которого J = 0.1 кг.м2 намотан шнур, к концу которого привязан груз массой m= 0,5 кг. До начала вращения барабана груз находился на высоте h = 1 м от пола. Через какое время груз опустится на пол. Трением пренебречь.
140. Два сплошных диска одинакового размера, изготовленные из алюминия и меди, вращаются независимо друг от друга вокруг общей неподвижной оси, проходящей через их центры, с угловыми скоростями ω1 = 5,0 рад /с и ω2 = 10 рад/с. С какой угловой скоростью ω вращались бы оба диска, если бы их жестко соединили. Плотность алюминия ρ1 = 2,6·103 кг/м3, плотность меди ρ2 = 8,6·103 кг/м3.
141. Человек массой m1 = 60 кг находится на неподвижной платформе массой m2=100 кг. С какой угловой скоростью ω будет вращаться платформа, если человек будет двигаться по окружности радиусом R1 =5 м вокруг оси вращения? Скорость движения человека относительно платформы v = 3,6 км/ ч. Радиус платформы R2= 10 м. Считать платформу однородным диском, а человека точечной массой.
142. Горизонтальная платформа массой m = 80 кг и радиусом R = 1 м вращается с угловой частотой 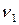 =20 об/мин. В центре платформы стоит человек и держит в расставленных руках гири. С какой частотой
=20 об/мин. В центре платформы стоит человек и держит в расставленных руках гири. С какой частотой 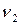 будет вращаться платформа, если человек, опустив руки, уменьшит свой момент инерции от J1 = 2,94 до J2 = 0.98 кгм2? Считать платформу однородным диском.
будет вращаться платформа, если человек, опустив руки, уменьшит свой момент инерции от J1 = 2,94 до J2 = 0.98 кгм2? Считать платформу однородным диском.
143. Платформа в виде диска радиусом R = 1 м вращается по инерции с частотой 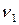 = 6 мин--1. На краю платформы стоит человек, масса которого равна m = 80 кг. С какой частотой
= 6 мин--1. На краю платформы стоит человек, масса которого равна m = 80 кг. С какой частотой 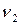 будет вращаться платформа, если человек перейдет в ее центр. Момент инерции платформы равен J=120 кг.м3. Момент инерции человека рассчитывать как для материальной точки
будет вращаться платформа, если человек перейдет в ее центр. Момент инерции платформы равен J=120 кг.м3. Момент инерции человека рассчитывать как для материальной точки
144. Человек стоит на скамье Жуковского и держит стержень, расположенный вертикально вдоль оси вращения скамейки. Стержень служит осью вращения колеса, расположенного на верхнем конце стержня, скамья неподвижна, колесо вращается с частотой 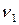 =10 с-1. Радиус колеса равен R = 20 cм, его масса m = 3 кг. Определить частоту вращения
=10 с-1. Радиус колеса равен R = 20 cм, его масса m = 3 кг. Определить частоту вращения 
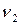 скамьи, если человек повернет стержень на угол f= 180о? Суммарный момент инерции человека и скамьи J= 6 кг.м2. Массу колеса можно считать равномерно распределенной по ободу.
скамьи, если человек повернет стержень на угол f= 180о? Суммарный момент инерции человека и скамьи J= 6 кг.м2. Массу колеса можно считать равномерно распределенной по ободу.
145. Обруч катится по горизонтальной дороге со скоростью v = 18 км/ч. На какое расстояние L он может подняться по наклонной плоскости за счет кинетической энергии, если уклон (отношение высоты наклонной плоскости к длине h/L) равен α = 0,10.
146. Маховик в виде диска начинает вращаться с угловым ускорением ε = 0,5 рад /с2 и через t1 = 20 с его кинетическая энергия становится равной W = 500 Дж. Какой момент импульса L приобретет он через t2 = 15 мин после начала движения?
147. Какой путь S пройдет катящийся без скольжения диск, поднимаясь вверх по наклонной плоскости с углом наклона α = 300, если ему сообщена начальная скорость v0 = 7,0 м/с, параллельная наклонной плоскости?
148. Какую мощность N должен развить мотор, приводящий в движение стабилизирующий гироскоп, который имеет форму диска радиусом R = 1,0 м и массой m = 1000 кг, если в течении t = 1 мин угловая скорость достигла значения ω = 31,4 рад/с. Трением и сопротивлением воздуха пренебречь.
149. На стержень диаметром d= 5 мм наглухо и соосно насажен сплошной диск диаметром D = 5 см и массой m = 0,4 кг. К стержню прикреплены нити, при помощи которых диск подвешивается к штативу. Найти ускорение, с которым опускается диск. Массой стержня пренебречь.
150. В дне цилиндрического сосуда имеется круглое отверстие диаметром d= 1 см. Диаметр сосуда D = 0,5 м. Найдите зависимость скорости v понижения уровня воды в сосуде от высоты h. Определите численное значение этой скорости для высоты h = 0,2 м.
151. Шарик всплывает с постоянной скоростью в жидкости, плотность которой в 4 раза больше плотности материала шарика. Во сколько раз сила трения, действующая на всплывающий шарик, больше силы тяжести шарика?
152. Стальной шарик диаметром d = 1 мм падает с постоянной скоростью v =0,185 см/с в большом сосуде, наполненном маслом. Определите коэффициент динамической вязкости масла. Плотность стали равна rc=8600 кг/м3, касторового масла - rк = 900 кг/м3.
153. В широкой части горизонтально расположенной трубы нефть течет со скоростью 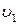 = 2 м/с. Определить скорость
= 2 м/с. Определить скорость 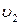 в узкой части трубы, если разность давлений в широкой и узкой частях ее равна DР = 6,65 кПа. Плотность нефти rк = 800 кг/м3.
в узкой части трубы, если разность давлений в широкой и узкой частях ее равна DР = 6,65 кПа. Плотность нефти rк = 800 кг/м3.
154. Горизонтальный цилиндр насоса имеет диаметр d1 = 20 cм. В нем движется со скоростью v1 = 1 м/с поршень, выталкивая воду через отверстие диаметром d2 = 2 см. С какой скоростью v2 будет вытекать вода из отверстия?. Каково будет избыточное давление воды Р в цилиндре?
155. Стальной канат, могущий выдержать вес неподвижной кабины лифта, имеет диаметр d = 12 мм. Какой диаметр должен иметь канат, если кабина лифта может иметь ускорение до 9g. Предел прочности стали σп =500 МПа.
156. Между двумя прочными упорами натянута стальная проволока диаметром 1 мм и длиной 2 м. На сколько сместится середина проволоки, если к ней подвесить груз массой 0,5 кг? Модуль Юнга для стали Е = 200 ГПа.
157. Какой диаметр d должен иметь стальной трос подъемного крана, если максимальная масса поднимаемого груза m= 10 т? Предел прочности стали σп = 500 МПа, запас прочности должен быть равен k =6.
158. Верхний конец стержня закреплен, а к нижнему подвешен груз массой m= 2кг. Длина стержня L = 5 м, сечение S = 4 см2. Определить напряжение материала стержня, его абсолютное ∆ L и относительное ε удлинение, если модуль Юнга Е = 2·1011 Па.
159. При океанологических исследованиях для взятия пробы грунта со дна океана на стальном тросе опускают особый прибор. Какова предельная глубина h погружения? Массой прибора пренебречь. Предел прочности стали σп = 500 МПа, плотность морской воды ρв = 1030 кг/м3, плотность стали ρс = 7800 кг/м3.
КОНТРОЛЬНАЯ РАБОТА № 2
ОСНОВНЫЕ ФОРМУЛЫ, НЕОБХОДИМЫЕ ДЛЯ РЕШЕНИЯ
i. ЭЛЕКТРОСТАТИКА
1. Закон сохранения электрических зарядов
В замкнутой системе:
Q =  = const.
= const.
2. Дискретность электрических зарядов:
Q = ne,
где n = 1, 2...; е = ± 1,6 . 10-19 Кл – элементарный электрический заряд
3. Закон Кулона
в векторной форме:
 ,
,
в скалярной форме:
 ,
,
где F12 - сила взаимодействия двух точечных (сферических) зарядов в вакууме; r - расстояние между зарядами или центрами сфер; ε0 = 8,85·10-12 Ф·/м - электрическая постоянная.
4. Линейная плотность зарядов:
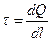 .
.  .
.
5. Поверхностная плотность зарядов:
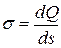 .
. 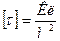 .
.
6. Объемная плотность зарядов:
 .
.  .
.
7. Напряженность электростатического поля:
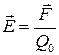 ,
, 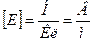 ,
,
где  - сила, действующая на точечный положительный заряд Q0, помещенный в данную точку поля.
- сила, действующая на точечный положительный заряд Q0, помещенный в данную точку поля.
8. Потенциал электростатического поля:
 ,
, 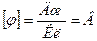 ,
,
где Wп - потенциальная энергия заряда Q0; A∞ - работа перемещения заряда из данной точки поля за его пределы.
9. Принцип суперпозиции:
Напряженность и потенциал результирующего поля, создаваемого системой точечных зарядов, равны соответственно:
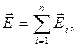
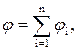
где Е1 и φi - напряженность и потенциал, создаваемый в данной точке поля зарядом Qi.
10. Разность потенциалов между двумя точками электростатического поля:
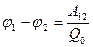 ,
,
где A12 – работа поля по перемещению заряда между точками 1 и 2.
11. Связь между напряженностью и потенциалом электростатического поля:
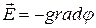 ,
,

 =
=  ,
,
где  - линейный интеграл напряженности электростатического поля.
- линейный интеграл напряженности электростатического поля.
12. Связь между напряженностью и потенциалом однородного поля:
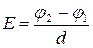 ; Δφ = Ed.
; Δφ = Ed.
13. Циркуляция вектора напряженности электростатического поля:

 ,
,
где Е l - проекция вектора E на направление элементарного перемещения dl. Интегрирование производится по любому замкнутому контуру.
14. Работа, совершаемая силами электростатического поля при перемещении заряда из точки 1 в точку 2:
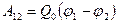 ,
,
A12 = Q0  Q0
Q0  .
.
15. Работа по перемещению точечного заряда Q в поле точечного заряда Q0:
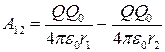 .
.
16. Работа по перемещению заряда в однородном электростатическом поле:
A12 = QEl cosα.
17. Поток вектора напряженности электростатического поля через элементарную площадку:
dN 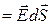 ,
,
dN = EdScos α = EndS,
где 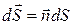 - вектор, модуль которого равен dS, а направление совпадает с нормалью
- вектор, модуль которого равен dS, а направление совпадает с нормалью 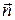 к площадке; En = Ecos α - составляющая вектора
к площадке; En = Ecos α - составляющая вектора  по направлению нормали к площади
по направлению нормали к площади
18. Поток вектора напряженности электростатического поля через произвольную поверхность:
NE = 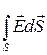 =
= 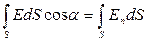 .
.
19. Теорема Гаусса для электростатического поля в вакууме:
NE= 
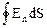 =
= 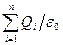 ,
,
в случае непрерывного распределения зарядов
NE = 
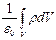 ,
,
где ε0– электрическая постоянная, Qi - алгебраическая сумма зарядов внутри поверхности; n-число зарядов; ρ - объемная плотность зарядов.
20. Применение теоремы Гаусса к расчету электрических полей.
| Система зарядов | Напряженность поля | Потенциал |
| Точечный заряд Q | E = Q/4πε0r2 | 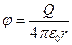
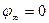
|
| Равномерно заряженная бесконечная плоскость с поверхностной плотностью зарядов σ | E = σ/2ε0 | 
|
| Две равномерно разноименно заряженные бесконечные плоскости, расположенные на расстоянии d | r ≤ 0, r ≥ d: E= 0 0 < r < d: E = σ/ε0 | 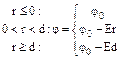
|
| Равномерно заряженная сфера радиусом R | 0 < r < R: E = 0 r = R: E = Q/4πε0R2 r > R: E = Q/4πε0r2 | 0 < r ≤ R: 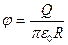 r > R:
r > R: 
|
| Равномерно объемно заряженный шар, радиусом R | 0 < r < R: E = Qr/4πε0R3 r = R: E = O/4πε0R2 r > R: E = Q/4πε0r2 | 0 < r < R:
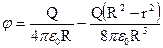 r = R: φ = Q/4πε0R
r > R: φ = Q/4πε0r r = R: φ = Q/4πε0R
r > R: φ = Q/4πε0r
|
| Равномерно заряженный бесконечный цилиндр радиуса R (нить) с линейной плотностью заряда τ | r < R: E = 0 r = R: E = τ/2πε0R; r > R: E = τ/2πε0r | r < R:  r > R:
r > R: 
|
21. Электроемкость уединенного проводника:
 ,
,  ,
,
где Q–заряд, сообщенный проводнику, φ - потенциал проводника.
Электроемкость проводника, помещенного в диэлектрик:
C = εC0.
22. Электроемкость шарового проводника:
C = 4πε0εR,
где R–радиус шара; ε - диэлектрическая проницаемость среды.
23. Электроемкость конденсатора:
C = 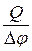 ,
,
где Q – заряд, сообщенный одной из обкладок; ∆φ - разность потенциалов между обкладками.
24. Емкость плоского конденсатора:
 ,
,
где S - площадь каждой пластины конденсатора; d – расстояние между пластинами.
25. Емкость системы конденсаторов:
последовательное соединение:
1/ C = 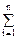 1/ Ci;
1/ Ci;
параллельное соединение:
C = 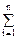 Ci,
Ci,
где Ci - емкость i-го конденсатора, n - число конденсаторов в батарее.
26. Энергия взаимодействия системы точечных зарядов:
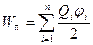 ,
,
где 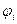 - потенциал, создаваемый всеми зарядами, кроме i–го в той точке, где находится заряд Qi.
- потенциал, создаваемый всеми зарядами, кроме i–го в той точке, где находится заряд Qi.
27. Энергия уединенного заряженного проводника:
 ,
,
где Q – заряд; C – электроемкость,  – потенциал проводника
– потенциал проводника
28. Энергия заряженного конденсатора:
 ,
,
где 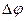 - разность потенциалов между обкладками.
- разность потенциалов между обкладками.
29. Энергия электростатического поля плоского конденсатора (однородное поле):
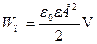 ,
,
где S– площадь одной из пластин; V = Sd - объем конденсатора
30. Объемная плотность энергии:
w = 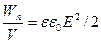 ;
;  .
.
II. ПОСТОЯННЫЙ ТОК
1. Сила и плотность электрического тока:
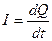 ,
,  ,
,  ,
,
где dQ – заряд, прошедший через поперечное сечение проводника за время dt.
2. Сопротивление R и проводимость G проводника:
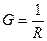 ,
, 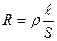 ,
,  ,
,
где ρ – удельное сопротивление; ℓ - длина проводника; γ – удельная проводимость; S – площадь поперечного сечения проводника.
3. Сопротивление системы проводников:
а) 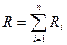 - при последовательном соединении,
- при последовательном соединении,
б) 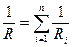 - при параллельном соединении,
- при параллельном соединении,
где Ri – сопротивление i-того проводника.
4. Законы Ома:
а)






