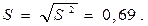
.
, 
Тогда 
.
Пусть 1- a =0,9. Тогда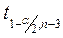 
= t 0,95;13 = 1,771. Поэтому:
.
Следовательно,
; 
.
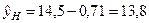Результаты вычислений целесообразно оформить в виде таблицы 2.4:
Таблица 2.4 - Прогноз
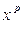
| Точечный прогноз | 
| Интервальный прогноз | |
| 
| 
| ||
| (1; 3; 165) | 14,5 | 0,40 | 13,8 | 15,2 |
2.5. На основании проведенных расчетов и полученных статистических характеристик можно сделать определенные выводы относительно взаимосвязей между исследуемыми экономическими показателями. Рассмотрим вначале зависимость цены от возраста. Так как 
=-0,78 и проверка значимости этого коэффициента показала его существенное отличие от нуля, то есть основания утверждать, что между переменными y и x1 существует достаточно тесная отрицательная линейная зависимость, которая может быть отражена с помощью найденного уравнения регрессии 
.
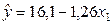Коэффициент a0 =16,1 в данном случае имеет экономический смысл. Он формально определяет цену при x1 =0, т.е. цену нового автомобиля.
Коэффициент a1 = -1,26 также имеет вполне определенный экономический смысл, поскольку характеризует размер прироста цены, обусловленного приростом возраста на единицу, т.е. при увеличении возраста на 1 год следует ожидать уменьшения цены на 1,26 тыс. у.е.
Необходимо особо подчеркнуть, что слова «следует ожидать снижения (прироста)...» в предыдущем предложении нельзя заменить словами «снижение цены составит...», так как уравнение регрессии y от x1 представляет собой лишь некоторую оценку стохастической зависимости между y и x1. Это уравнение характеризует так называемое среднее значение цены в зависимости от возраста автомобиля. Слово «среднее» выражает здесь тот факт, что реальное значение цены yi, соответствующее некоторому реальному возрасту xi1, будет находиться в некоторой окрестности значения .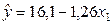
Значимое значение 
= 0,44 (см. п.1.2) свидетельствует о том, что между y и x2 существует достаточно тесная линейная зависимость. Экономический смысл коэффициента b1 в уравнении 
аналогичен смыслу коэффициента a1 в уравнении 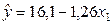, т.е. b1 показывает, какого прироста цены следует ожидать при увеличении мощности двигателя на единицу – на 1 л.с.
В результате исследования зависимости объема цены от двух факторов - возраста и мощности двигателя, получено уравнение множественной регрессии 
.
Содержательный смысл найденных коэффициентов уравнения состоит в следующем. Величина a1 = -1,42 показывает, что при увеличении возраста на 1 год и фиксированной (неизменной) мощности двигателя следует ожидать снижения цены автомобиля на 1,42 тыс. у. е.
Коэффициент a2 =0,05 показывает, что при увеличении мощности двигателя на 1 л.с. и фиксированном возрасте следует ожидать увеличения цены на 0,05 тыс. у. е.
Сравнение результатов, полученных на основе анализа уравнений парной регрессии, с результатами, полученными на основе анализа уравнения множественной регрессии, может создать представление об их противоречивости, поскольку оценки параметров заметно различаются. Однако здесь нет противоречия. Действительно, исследуя зависимость 
, мы исходим из того, что на цену влияет один единственный фактор – возраст автомобиля, а все остальные объясняющие факторы не учитывались (отбрасывались). Очевидно, что в реальности на цену влияет множество факторов: вес автомобиля, расход топлива, время разгона, регион производителя и т.д. Поэтому, рассматривая модель , мы фактически объединили все влияющие на y факторы в один результирующий и назвали этот фактор возрастом автомобиля. Точно такое же объединение всех факторов в один результирующий фактор было осуществлено при рассмотрении модели 
. Поэтому коэффициенты, отражающие степень (или силу) влияния каждого из двух рассмотренных факторов в отдельности на зависимую переменную, оказались достаточно большими.
Для более точного описания изменения исследуемого показателя следует включать в эконометрическую модель по возможности большее количество объясняющих переменных (факторов). Вместе с тем, увеличение количества объясняющих факторов должно проводиться достаточно осторожно. С одной стороны, в числе этих факторов может оказаться такой, который не оказывает сколько-нибудь существенное влияние на объясняемую переменную y. С другой стороны, математическая модель может оказаться слишком громоздкой и неудобной для анализа. Существуют различные методы выявления и отбора существенных факторов. Простейший основан на вычислении и анализе коэффициентов парной корреляции 
, ,..., 
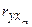, где y - результирующий признак, а x1, x2,..., xm, - объясняющие факторы. Другой подход основан на рассмотренном дисперсионном анализе модели.
Следует помнить, что прежде, чем применять формальные, математические методы отбора и выявления существенных факторов, следует провести тщательный содержательный анализ изучаемого объекта или процесса.
Используемое в задачах 1 и 2 понятие доверительной вероятности характеризует степень уверенности в справедливости получаемого результата. Чем ближе к единице значение доверительной вероятности (1- a), тем с большей уверенностью можно утверждать, что прогнозируемое значение результирующего признака будет находиться в найденном доверительном интервале. Следует иметь в виду, что ширина доверительного интервала существенно зависит от значения (1- a): чем ближе к единице величина (1- a), тем шире доверительный интервал и, следовательно, хуже качество прогноза.
Очевидно, что достаточно широкий доверительный интервал прогноза не имеет никакого практического значения. Действительно, если мы получим результат типа:
«С вероятностью 0,999 среднее значение цены будет находиться в пределах от 0 до 20 тыс. у. е.», то от такого результата нет никакой практической пользы. При этом степень его достоверности оценивается в 99,9%. Поэтому при определении интервального прогноза приходится искать разумный компромисс между качеством прогноза, т.е. шириной доверительно интервала, и его достоверностью, т.е. значением доверительной вероятности.
Задача 3. Временные ряды
Необходимые сведения. В задачах 1 и 2 значения зависимой переменной yi (i =1,2,…, n) независимы и одинаково распределены. Значения временных рядов yt (t =1,2,…, n) как правило, зависимы и в каждый момент t имеют разные распределения.
На графике траектория временного ряда, как правило, носит упорядоченный характер. Нет ансамбля реализаций. Все статистические выводы могут делаться только по одной траектории.
3.1. На рисунке 3.1 представлены ежегодные значения объема продаж автомагазина из таблицы 0.2 исходных данных за пять лет.
На основании визуального наблюдения ломаной линии динамики продаж можно сделать вывод, что каждый год объем продаж возрастает примерно на 300 тыс. у.е. То есть можно выдвинуть гипотезу о существовании линейного тренда - устойчивого роста среднего уровня временного ряда:
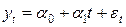, (3.1)
Рисунок 3.1 - Траектория временного ряда
где a0, a1 - неизвестные параметры, εt - случайные возмущения. Как и в задаче 1, приходим к рассмотренной выше системе нормальных уравнений МНК (1.1), в которой вместо объясняющей переменной xi,1 под знаками сумм будут стоять значения времени t.
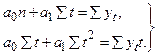(3.2)
Коэффициенты регрессионного уравнения тренда 
находятся из этой системы аналогично формулам (1.2) - (1.4):
, 
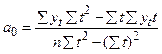. (3.3)
Если временные отсчеты представляют собой натуральный ряд t=1,2,…,n, то суммы степеней времени t можно заранее рассчитать, если известно n:
. (3.4a)
. (3.4b)
Решение задачи. Сформируем таблицу промежуточных расчетов по формуле (3.3), (таблица 3.1):
Таблица 3.1
| t | yt | yt t | t2 |
| Сумма=15 |
Первый и последний столбец в таблице 3.1 можно не формировать. Действительно, итог по первому столбцу в силу (3.4a) равен:
.
Итог по последнему столбцу можно рассчитать по формуле (3.4b):
.
Квадрат суммы t равен 15×15=225. Подставляя полученные значения в (3.3), получим:
;
.
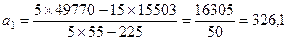Следовательно, уравнение тренда (регрессии) будет иметь вид
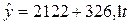. (3.5)
Тот же результат получим, используя функцию «Добавить линию тренда» в редакторе диаграмм Microsoft Excel, см. рисунок 3.2. На закладке «Тип» появившегося окна «Линия тренда» нужно выбрать линейный тип уравнения в соответствии с выдвинутой нами ранее гипотезой о линейном тренде, рисунок 3.3. На закладке «Параметры» этого окна, как и прежде, включим показ уравнения и коэффициента детерминации R2. Кроме того, в панели «Прогноз» зададим упреждение «на 1 единицу вперед», то есть на один год вперед, рисунок 3.4. Таким образом, видим, что Microsoft Excel может показывать на графике точечный прогноз тренда. При этом численное значение точечного прогноза, к сожалению, не выводится.
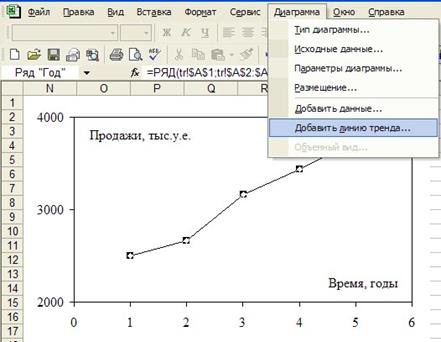
Рисунок 3.2 - Вставка тренда на диаграмму
Рисунок 3.3 - Закладки «Тип» и «Параметры» окна «Линия тренда»
Результат оценки тренда и точечный прогноз, полученный в редакторе диаграмм в Microsoft Excel, показан на рисунке 3.4. Видим, что результаты ручного расчета в (3.5) и в MS Excel близки. Различие наблюдается только в пятом незначащем разряде.
Еще один недостаток Microsoft Excel заключается в том, что он не дает доверительные интервалы тренда и прогноза. Их придется рассчитать «вручную». Последнее слово взято в кавычки, поскольку этот расчет можно реализовать в том же Microsoft Excel.
Рисунок 3.4 - Результат оценки тренда и прогноз в Microsoft Excel
3.2. Доверительный интервал для линейного тренда 
находится так же, как и в задаче 1, по формуле, аналогичной (1.7):
, (3.6)
где
, 
,
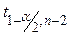- квантиль распределения Стьюдента, (1-a) - доверительная вероятность;
t - номер временного отсчета (в нашем примере – года), для которого определяется доверительный интервал;
- выборочное среднее временных отсчетов.
Для расчета доверительных интервалов составим таблицу 3.2.
Таблица 3.2
| t | yt | 
| et | et2 | t-tcp | (t-tcp)2 |  Н
| В
|
| -2 | ||||||||
| -111 | -1 | |||||||
| -8 |
Для определения квантиля распределения Стьюдента 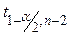, используемого в (3.6) и в таблице 3.2, снова придется обратиться к соответствующим таблицам [2,4,7,9], В нашем случае t0,95;3 =2,353.
В нашем примере =3. S2 =6260. S =79,12. Доверительные интервалы на интервале ретроспекции, использующие эти значения, рассчитаны в двух последних столбцах таблицы 3.2.
Рисунок 3.5 - Тренд и доверительные интервалы
На рисунке 3.5 изображены график тренда (третий столбец таблицы 3.2), доверительные интервалы для t =1,2,3,4,5 и доверительная полоса, соединяющая эти доверительные интервалы.
3.3. Точечный прогноз среднего значения продаж по линейному тренду находится для t= 6 по формуле (3.5):
=2122+326,1×6=4079 тыс. у.е. (3.7)
Для определения интервального прогноза рассчитаем при t= 6 значение
.
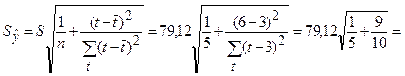
Таким образом, окончательно получаем интервальный прогноз продаж:
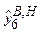=4079 ± 2,353×82,98=4079 ± 195,3 тыс. у.е.,
или 
= 3884 тыс. у.е., 
= 4274 тыс. у.е.
3.4. Прогноз среднегодового значения продаж, конечно, полезен для предприятия. Однако, в силу постоянно растущей неопределенности современной экономики, намного важнее принимать управленческие решения как можно чаще. Для этого нужно знать прогнозы на ближайшие кварталы, месяцы и даже дни. Современные информационные системы позволяют вести учет с такой дискретностью, и предприятия стали обладать данными для разработки эконометрических моделей с такой детализацией.
На рисунке 3.6 показана траектория рассмотренного выше (рис. 3.1 – 3.5) временного ряда объема продаж за пять лет, но данные представлены с дискретностью в один месяц, начиная с января. Численные значения этого ряда приведены в таблице 0.3 исходных данных.
Рисунок 3.6 - Динамика продаж по месяцам
На основании визуального наблюдения ломаной линии динамики ежемесячных продаж можно выдвинуть две гипотезы о тенденциях ломаной линии динамики продаж.
Первую гипотезу о существовании линейного тренда - устойчивого роста среднего уровня временного ряда
,
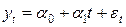мы уже выдвигали в (3.1), подтвердили ее и оценили неизвестные параметры a0, a1. Оценка a1 составила 326 тыс. у.е. То есть на эту величину продажи возрастают в среднем ежегодно. Понятно, что и в ряде на рис. 3.8 присутствует этот тренд. Ежемесячный рост или оценка a1 нового тренда должна быть на уровне 326/12=27 тыс. у.е.
Вторая гипотеза заключается в существовании сезонного (периодического) тренда
. (3.8)
Период T сезонной волны в (3.8) известен и составляет 12 месяцев.
В этой модели присутствуют одновременно косинус и синус, чтобы учесть фазу процесса. Если бы в (3.8) мы оставили только косинус, то максимальные значения сезонной волны соответствовали бы январю. В действительности пик продаж не приходится на первое наблюдение (январь). Максимальные продажи наблюдаются в апреле – мае, в момент максимального спроса и движения автомобильного рынка. Этот сдвиг пика сезонной волны и учитывает синус модели.
Обе гипотезы можно выразить одной трендово - сезонной моделью:
. (3.9)
Эта модель линейна по параметрам a. Объясняющих переменных здесь три:
x1 = t, x2 =cos(2π t /12 ), x3 =sin(2π t /12 ). (3.10)
Все они являются известными функциями временных отсчетов t и могут быть вычислены. Параметры могут быть оценены по стандартной схеме (2.3) метода наименьших квадратов для множественной регрессии, описанной в задаче 2. При этом количество столбцов в матрице X увеличится до четырех.
Матрица XTX и столбец XTY в (2.2) примут вид:
;
. (3.11)
Напомним, чтобы найти вектор оценок параметров для модели (3.9), нужно обратить матрицу XTX в (3.11) и результат умножить на столбец XTY в (3.11) в соответствии с формулой (2.3): 
.
Для этого, как и в задачах 1 и 2, составим таблицу, содержащую колонки, необходимые для расчета всех сумм в (3.11):
- колонки с зависимой и объясняющими переменными:
yt, t, cos(2π t /12 ), sin(2π t /12 ),
- дополнительные колонки:
t2, t cos(2π t /12 ), t sin(2π t /12 ), cos2(2π t /12 ), sin2(2π t /12 ), cos(2π t /12 ) sin(2π t /12 ),
yt t, yt cos(2π t /12 ), yt sin(2π t /12 ).
Фрагмент этой таблицы представлен ниже (таблица 3.3).
Фрагмент формирования таблицы в Microsoft Excel представлен на рисунке 3.7.
Таблица 3.3 – Расчет элементов матрицы XTX и столбца XTY
| Мес. | y | t | Cos | Sin | t2 | t Cos | t Sin | Cos2 | … | y Cos | y Sin |
| 0,87 | 0,50 | 0,87 | 0,50 | 0,75 | … | 153,29 | 88,50 | ||||
| 0,50 | 0,87 | 1,00 | 1,73 | 0,25 | … | 124,00 | 214,77 | ||||
| 0,00 | 1,00 | 0,00 | 3,00 | 0,00 | … | 0,00 | 265,00 | ||||
| … | … | … | … | … | … | … | … | … | … | ||
| 1,00 | 0,00 | 60,00 | 0,00 | 1,00 | … | 294,00 | 0,00 | ||||
| Сумма | 0,00 | 0,00 | 30,00 | -112,0 | 30,00 | … | -1396 |
Вместо значений на рисунке 3.7 специально показаны расчетные формулы (3.10). Строки с наблюдениями 5-58 для экономии места скрыты. В столбце А введены номера месяцев (временных отсчетов), в столбце B - значения продаж из таблицы 0.3 исходных данных. В столбце С сформирована объясняющая переменная x1 = t, численно совпадающая со столбцом А. В столбцах D и E сформированы объясняющие переменные x2 =cos(2π t /12 ) и x3 =sin(2π t /12 ) по формулам (3.10).
Рисунок 3.7 - Фрагмент формул для расчета
Подставим суммы, полученные с помощью этих таблиц в (3.11):
. 
. (3.12)
Обратить матрицу XTX можно с помощью функции МОБР Microsoft Excel. Схема использования этой функции аналогична схеме использования функции ЛИНЕЙН, рассмотренной ранее в 1.4.1.
Предполагается, что данные матрицы XTX уже введены. Далее нужно выполнить следующие действия:
1) выделите область пустых ячеек 4×4 для вывода обратной матрицы;
2) активизируйте Мастер функций, например, кнопкой Вставка функции;
3) в выпадающем списке «Категория» выберите Математические, в окне выбора функции - МОБР. Нажмите ОК.
4) в окне аргументов функции задайте адреса массива, в котором введены данные матрицы XTX; щелкните по кнопке ОК;
5) в левой верхней ячейке выделенной области появится первый элемент обратной матрицы.
Чтобы раскрыть всю матрицу, нажмите на клавишу <F2>, а затем на комбинацию клавиш <Ctrl>+<Shift>+<Enter>. В заданную область рабочего листа будет выведена обратная матрица (XTX) -1:
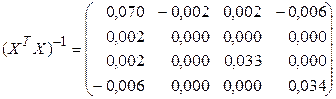. (3.13)
Окончательно получим оценки параметров (функция МУМНОЖ):
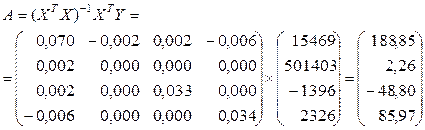. (3.14)
Оценим модель (3.9) менее трудоемким способом. Запускаем раздел «Регрессия» Пакета анализа данных Microsoft Excel, см. рисунок 3.8.
Рисунок 3.8 - Формирование раздела «Регрессия»
В таблицах 3.4-3.5 приведены результаты регрессионного анализа Microsoft Excel. Технология расчетов в таблицах показана ранее в задачах 1-2.
Таблица 3.4 - Коэффициенты модели
| Коэффи- циенты | Стандартная ошибка | t-стати- стика | P-Зна- чение | Нижние 95% | Верхние 95% | |
| Y-пересе- чение | 5,68 | 33,2 | 0,000 | |||
| t | 2,26 | 0,162 | 13,9 | 0,000 | 1,94 | 2,59 |
| Cos | -48,8 | 3,93 | -12,4 | 0,000 | -56,7 | -40,9 |
| Sin | 86,0 | 3,97 | 21,6 | 0,000 | 78,0 | 93,9 |
Оценки параметров в таблице 3.4 совпадают с результатами (3.14).
Значения t -статистик Стьюдента и вероятностей P принятия нулевой гипотезы H0 позволяют отвергнуть ее для каждого параметра в пользу альтернативной. Таким образом, все параметры значимы, и их необходимо включать в модель. Запишем ее окончательный вид:
. t =1,2,…,60. (3.15)
R -квадрат равен 0,93. Дисперсионный анализ модели представлен в таблице 3.5. F – критерий Фишера так же высок. Все это говорит о высокой значимости модели.
Таблица 3.5 - Дисперсионный анализ
| df | SS | MS | F | Значимость F | |
| Регрессия | 335034,9 | 111678,3 | 241,3 | 0,000 | |
| Остаток | 25918,11 | 462,8234 | |||
| Итого |
На рисунке 3.9 показаны тренд и сезонная волна из (3.15).
Рисунок 3.9 - Трендово – сезонная модель продаж
Рассчитаем точечный прогноз объема продаж на год, то есть на 12 месяцев вперед. Для этого экстраполируем модель (3.15) на 12 месяцев вперед:
. t =61,62,…,72. (3.16)
Результаты прогнозирования по (3.16) представлены в таблице 3.6. Сумма прогнозов за 12 месяцев составляет 4072 у.е. Это практически совпадает со значением 4079 тыс. у.е., полученным по трендовой модели (3.7) с годовой дискретностью. Близость результатов двух разных моделей повышает уверенность в качестве прогнозов.
Таблица 3.6 - Точечный прогноз объема продаж на 12 месяцев
| t, мес. | ||||||||||||
| Прогноз, тыс. у.е. |
3.5. Интервальный прогноз среднего значения объема продаж, как и в случае множественной регрессии (2.6), находится по формуле:
, где (3.17)
, 
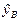- соответственно верхняя и нижняя границы доверительного интервала,
-вектор значений независимых переменных (как на интервале ретроспекции, так и на интервале упреждения),
- квантиль распределения Стьюдента, (1 -a) - доверительная вероятность, n - количество наблюдений, (n- 4) - число степеней свободы,
(3.18)
, 
, 
определен в (3.15) и (3.16).
Определяем вектор независимых переменных , для первого прогнозного месяца:
x61 = (1, 61, cos(2π×61/12), sin(2π×61/12)) = (1, 61, 0,866, 0,500).
Точечный прогноз нами уже найден в первой числовой колонке таблицы 3.6 на основе (3.16):
= 189×1 + 2,26×61 - 48,8×cos(2π×61/12) + 86,0×sin(2π×61/12) =
= 189×1 + 2,26×61 - 48,8×0,866 + 86,0×0,500 = 328.
Вычислим подкоренное значение в формуле (3.18). Для перемножения матриц, как и раньше, можно воспользоваться функцией МУМНОЖ Microsoft Excel. Сначала перемножим вектор-строку и квадратную матрицу:
.
Затем полученную вектор-строку умножим на вектор-столбец:
.
Извлечем корень: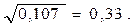 
Далее для расчета среднеквадратического отклонения остатков таблицу 3.3 нужно дополнить столбцом остатков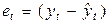 
и столбцом квадратов остатков 
. Для экономии места здесь их не приводим. Суммируя столбец квадратов остатков, получим:
. 
Тогда 
.
Пусть 1- a =0,9. Тогда = t 0,95;56 = 1,673. Поэтому:
.
Или: 
; 
.
Аналогично рассчитывается интервальный прогноз для t =61,62,…,72.
Результаты вычислений оформим в виде таблицы 3.7. Поскольку расчеты даже в Microsoft Excel громоздки, в контрольной работе достаточно привести только одну первую строку таблицы 3.7.
Таблица 3.7 - Точечный и интервальный прогноз
| t |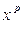
| Точечный прогноз |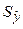 
| Интервальный прогноз | |
| (1; t; cos(2π× t /12); sin(2π× t /12)) |
|
|
| ||
| (1; 61; 0,87; 0,50) | 7,02 | ||||
| (1; 62; 0,50; 0,87) | 7,35 | ||||
| (1; 63; 0,00; 1,00) | 7,60 | ||||
| … | … | … | … | … | … |
| (1; 72; 1,00; 0,00) | 8,15 |
Точечный и интервальный прогноз среднего значения продаж, рассчитанный в таблице 3.7, показан на рисунке 3.10.
Рисунок 3.10 - Точечный и интервальный прогноз среднего значения продаж
Задача 4. Проверка моделей на автокорреляцию
и мультиколлинеарность
4.1. Необходимые сведения. В качестве одного из предположений, лежащих в основе применения метода наименьших квадратов и обеспечивающих хорошие свойства оценок неизвестных параметров моделей, используется независимость, или некоррелированность случайных отклонений (возмущений). В приведенных выше эконометрических моделях возмущения обозначались через ε и d. Если последовательные значения ei случайного отклонения в i -м наблюдении коррелируют между собой, то говорят, что имеет место автокорреляция ошибок (остатков).
Автокорреляция обычно встречается в регрессионном анализе при использовании данных временных рядов. Случайный член ε в регрессионной модели 
подвергается воздействию тех переменных, влияющих на зависимую переменную, которые не включены в модель.
К основной причине, вызывающей появление автокорреляции, относятся ошибки спецификации, под которыми понимают либо отсутствие в модели важной объясняющей переменной, либо неправильный выбор формы зависимости, что зачастую приводит к системным отклонениям точек наблюдений от линии регрессии и появлению автокорреляции.
Проверка наличия или отсутствия автокорреляции ошибок регрессии проводится с помощью статистики Дарбина-Уотсона, которая имеет вид
, (4.1)
где 
- отклонения от линии регрессии, t=1,2,…n.
Схема проверки такова. Расчетное значение d - статистики Дарбина-Уотсона сравнивается с нижним - dl, и верхним - du значениями. Необходимые для предлагаемых задач значения dl и du приведены в таблице 4.1.
Таблица рассчитана для уровня значимости a=0,05. В таблице 4.1 n - число наблюдений, m - число объясняющих переменных.
Таблица 4.1
| m= 1 | m= 2 | m= 3 | ||||
| n | dl | du | dl | du | dl | du |
| 1,10 | 1,37 | 0,98 | 1,54 | 0,82 | 1,75 | |
| … | … | … | … | … | ||
| 1,55 | 1,62 | 1,51 | 1,65 | 1,48 | 1,69 |
Если du<d<4-du, то делается вывод об отсутствии автокорреляции.
Если dl<d<du, или 4-du<d<4-dl, то ничего нельзя сказать о наличии или отсутствии автокорреляции.
Если d< dl или d>4- dl, то делается вывод о наличии автокорреляции.
Поясняет эту схему рисунок 4.1.
| Положительная автокорреляция | Зона неопределенности | Автокорреляция отсутствует | Зона неопределенности | Отрицательная автокорреляция | |||
| dl | du | 4- du | 4- dl | ||||
| 3 4 | |||||||
Рисунок 4.1 - Зоны работы статистики Дарбина-Уотсона
Решение задачи. Рассмотрим множественную регрессионную модель
.
Напомним, в задаче 2 мы нашли модель (2.5) зависимости цены автомобиля от его возраста и мощности двигателя:
.
Проверим, имеет ли место автокорреляция ошибок этой модели. Найдем значения числителя и знаменателя в формуле (4.1). Значение знаменателя найдено ранее при решении задачи 2.3, и равно 6,21. Значение числителя в формуле d - статистики Дарбина-Уотсона (4.1) легко вычисляется и равно 9,40. Подставляя найденные значения в (4.1), получим
d = 9,40 / 6,21 =1,51.
В исследуемой ситуации число наблюдений n=16, число объясняющих (независимых) переменных m=2. По условию уровень значимости a=0,05. По таблице 4.1 находим: dl =0,98; du =1,54. В нашем случае dl < d < du. Статистика Дарбина-Уотсона находится в зоне неопределенности. Всего три-четыре сотых не хватает для того, чтобы можно было уверенно принять гипотезу об отсутствии автокорреляции ошибок регрессии.
Рассмотрим уравнение (3.11):
.
В этой задаче n =60, m =3. Уровень значимости a =0,05.Расчетное значение d - статистики Дарбина-Уотсона равно:
d = 42393 / 25918 = 1,64.
Табличные критические значения dl = 1,48, du = 1,69.Поэтому dl< d <du. Как и в предыдущем примере d - статистика Дарбина-Уотсона находится в зоне неопределенности. Гипотезу об отсутствии автокорреляции нельзя уверенно принять.
Основная причина появления автокорреляции - это ошибки спецификации. Поэтому методы устранения этого явления сводятся к исключению причин его возникновения. Во-первых, следует проанализировать, не упущен ли из рассмотрения какой-либо важный фактор или несколько факторов, влияющих на изменение зависимой переменной. Если такой фактор выявлен, следует рассмотреть новую модель с учетом новой объясняющей переменной, найти оценки неизвестных параметров модели и вновь проверить наличие или отсутствие автокорреляции. Во-вторых, можно попробовать изменить форму модели. Например, вместо линейной рассмотреть квадратичную или логарифмическую. При этом новая форма модели может быть исследована как с первоначальным набором независимых (объясняющих) переменных, так и с новым, расширенным набором.
4.2. Необходимые сведения. Под мультиколлинеарностью понимается наличие нестрогой линейной зависимости между объясняющими переменными. Такая линейная зависимость может привести к получению ненадежных оценок неизвестных параметров модели.
Проблема мультиколлинеарности может возникнуть только в уравнениях множественной регрессии, когда исследуется зависимость между объясняемой переменной y и несколькими объясняющими переменными x1, x2,..., xm. Как известно, тесноту линейной взаимосвязи между двумя случайными переменными можно измерить с помощью коэффициента корреляции - чем теснее линейная зависимость между переменными, тем ближе значение коэффициента корреляции к единице. О переменных, находящихся в достаточно (или относительно) тесной линейной зависимости, говорят, что они коррелируют между собой. Наличие корреляции между объясняющими переменными затрудняет разделение их влияния на поведение зависимой переменной. Этот вывод можно проиллюстрировать с помощью рисунка 4.2.
На рисунке 4.2а коррелированность между объясняющими переменными x1 и x2 отсутствует, и влияние каждой из них на у находит отражение в наложении кругов x1 и x2 на круг у. По мере усиления линейной зависимости между x1 и x2 соответствующие круги все больше накладываются друг на друга. Заштрихованная область отражает совпадающие части влияния x1 и x2 на y. На рисунке 4.2г отражен случай строгой (функциональной) линейной зависимости между x1 и x2, и здесь невозможно разграничить степени индивидуального влияния объясняющих переменных x1 и x2 на результирующий признак y.
Одним из простейших методов определения мультиколлинеарности является вычисление и анализ коэффициентов парной корреляции между всеми парами объясняющих переменных - 
, 
,..., 
, 
,... 
,..., 
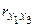, которые можно представить в виде матрицы
. (4.2)
Рисунок 4.2 - Геометрическая интерпретация мультиколлинеарности
Поскольку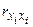 
=1, то на главной диагонали матрицы r расположены единицы.
Если для некоторых i ¹ j значения | 
| близки к единице, то можно предполагать, что переменные xi и xj коррелируют между собой, то есть между ними имеется нестрогая линейная зависимость и, следовательно, имеет место мультиколлинеарность.
Для оценки мультиколлинеарности объясняющих переменных можно использовать определитель Det (r) матрицы r коэффициентов парной корреляции.
Если объясняющие переменные не коррелируют между собой, то все недиагональные элементы в (4.2) равны нулю, и Det (r) = 1. Если, наоборот, между объясняющими переменными существует полная линейная зависимость и все коэффициенты парной корреляции равны единице, то Det (r) = 0.
Чем ближе Det (r) к нулю, тем сильнее мультиколлинеарность. И, наоборот, чем ближе Det (r) к единице, тем меньшее мультиколлинеарность факторов.
Нулевая гипотеза о независимости объясняющих переменных формулируется следующим образом: H0: Det (r) = 1.
Проверка гипотезы производится на основе статистики хи-квадрат. Если фактическое значение статистики не превышает табличного (критического) для степеней свободы df и уровня значимости α, то есть χ2факт < χ2табл(df, α), то гипотеза H0 принимается, и делается вывод об отсутствии мультиколлинеарности. В противном случае делается вывод о сущесвовании мультиколлинеарности. Фактическое значение статистики рассчитывается по формуле:
(4.3)
Здесь, как и раньше, n - количество наблюдений, m - число объясняющих переменных.
Число степеней свободы определяется по формуле:
Для устранения мультиколлинеарности разработаны разнообразные методы. Однако отметим, что в ряде случаев мультиколлинеарность не является настолько существенным недостатком исследуемой модели, чтобы прилагать значительные усилия по ее выявлению и устранению. В основном все зависит от целей исследования.
Если основная задача исследования модели состоит в получении прогнозов будущих значений зависимой переменной, то при достаточно большом коэффициенте детерминации наличие мультиколлинеарности мало скажется на прогнозных качествах модели. Если же целью исследования является определение степени влияния каждой из объясняющих переменных на зависимую переменную, то наличие мультиколлинеарности, скорее всего, исказит истинные зависимости между переменными. Отметим также, что не существует единого универсального метода устранения мультиколлинеарности, который был бы пригоден в любом случае.
Решение задачи. Рассмотрим уравнение регрессии 
, выражающее зависимость цены автомобиля от его возраста и мощности двигателя. В нашем случае коэффициент парной корреляции между объясняющими переменными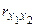 
=0,17. Этот коэффициент незначимо отличается от нуля. Действительно:
оэтому можно считать, что переменные x1 и x2 не коррелируют между собой и, следовательно, нет мультиколлинеарности.
Рассчитаем определитель матрицы (4.2) коэффициентов парной корреляции:
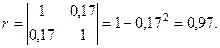
По формуле (4.3) получим:
Табличное значение статистики для df = 1 и α = 0,05 равно χ21;0,05 = 3,84. Неравенство χ2факт < χ2табл(df, α) выполняется. Поэтому окончательно делаем вывод об отсутствии мультиколлинеарности.
И в заключении обратим внимание на то, что в прочитанном Вами тексте часто встречались термины типа: «достаточно близко к...», «достаточно мал (или велик)», «следует ожидать, что...», «достаточно тесная зависимость», «с 90%-й уверенностью» и т.д. Наличие таких терминов может создать ошибочное впечатление о низкой надежности или научности рассмотренного в данной работе математического аппарата, и его применения к исследованию реальных экономических проблем. Поэтому необходимо осознать, что реальные экономические и социально-экономические задачи сложны, многообразны, подвержены влиянию огромного множества факторов, в том числе случайных. И результаты решения таких задач зачастую не могут быть выражены одним единственным числом, или строго (в математическом смысле) заданной формулой. Не могут быть они выражены и утверждениями типа: «если среднегодовой доход на одного жителя России в 2007 г. составит 90 тыс. руб., то каждый житель Новосибирской области затратит в этом году на приобретение одежды и обуви 14772 рубля».
В эконометрике многие результаты, и особенно касающиеся прогнозов, справедливы лишь с некоторой надежностью. Чем выше надежность какого-либо утверждения, результата, события, тем с большей уверенностью их можно применять на практике. В этой специфике эконометрики заключено ее преимущество, а не недостаток, поскольку эконометрические методы и модели предназначены для отражения и исследования реальных процессов в экономической и социальной сферах деятельности человека.
ЛИТЕРАТУРА
1.
2. Айвазян С.А., Мхитарян В.С. Прикладная статистика и основы эконометрики. - М.: ЮНИТИ, 1998.
3. Доугерти К. Введение в эконометрику: Учебник. 2-е изд. / Пер. с англ. – М.: ИНФРА-М, 2004. – 432 с.
4. Эконометрика: Учебник / Под ред. И.И. Елисеевой -М.: Финансы и статистика, 2004. – 344 с.
5. Практикум по эконометрике: Учеб. пособие / И.И. Елисеева, С.В. Курышева, Н.М. Гордиенко и др.; Под ред. И.И. Елисеевой - М.: Финансы и статистика, 2004. – 192 с.
