асть III. Проектирование соответствующего цифрового фильтра.
1. Определение интервала дискретизации ЦФ.
2. Получение системной функции ЦФ.
3. Получение модуля частотной характеристики ЦФ.
4. Получение импульсной и переходной характеристик ЦФ.
5. Проверка устойчивости АФ и ЦФ.
6. Построение структурной канонической схемы ЦФ.
7. Реализация ЦФ программным путем.
ешение разностного уравнения 2-го порядка векторно-матричным способом с использованием Z-преобразования
раткие теоретические сведения
Переход от разностного уравнения n-го порядка к векторно-матричному уравнению
Пусть дано разностное уравнение 2-го порядка:

Разрешаем его относительно Un+2:

Вводим обозначения:
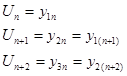
Получим следующую систему

В матричной форме данная система записывается следующим образом:
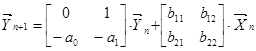

Решение векторного разностного уравнения с помощью Z-преобразования
Осуществляем Z-преобразование:


Определим вектор 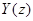 :
:


В дальнейшем осуществляется переход от Z-изображения к оригиналу:
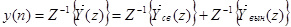
1.2 Задано разностное уравнение:

Разрешаем его относительно xn+2:

н.у.: x0 = 5; x1 = 7
1) Введем обозначения:

Получаем:

Запишем систему в векторно-матричной форме:
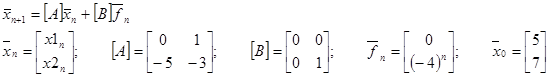
1.3 Получение решения РУ матричным методом с помощью
Z-преобразования

а) Получение изображений
Определяем матрицу  на MathCad:
на MathCad:


Найдем матрицу  , используя метод Фадеева.
, используя метод Фадеева.

| 

| 

|
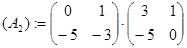

| 
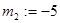
| 

|


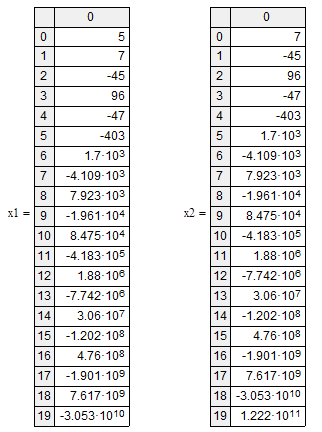
б) Нахождение оригиналов


Используя обратное Z-преобразование и комплексное вычисление находим:

Проверка (Нахождение оригиналов "вручную"):
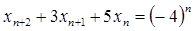
Разрешаем его относительно xn+2:

н.у.: x0 = 5; x1 = 7
1) Введем обозначения:

Получаем:

Запишем систему в векторно-матричной форме:
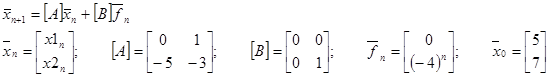








Часть II.Проектирование аналогового фильтра –прототипа, отвечающего требованию обработки сигнала и заданной частоте среза (100Гц)
1. Передаточная функция АФ

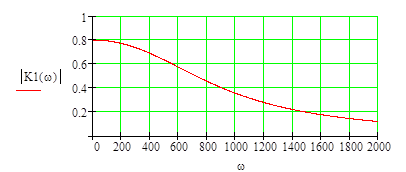
2. Частотная характеристика АФ

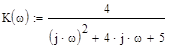


3. Приведение передаточной функции к стандартному виду







4. Переход к заданной частоте:

|

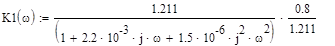
5. Расчет элементов АФ




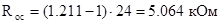

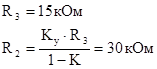
Схема ФНЧ на EWB 5.1:

Диаграмма БОДЕ

АЧХ

Импульсная характеристика:

|
Переходная характеристика:


асть III. Проектирование соответствующего цифрового фильтра.
Краткие теоретические сведения
Цифровой фильтр – это цифровая система, преобразующая дискретную последовательность в соответствии с заданным алгоритмом. Цифровой фильтр может быть реализован программным путем на ЭВМ или с помощью специальной аппаратуры. И в том и в другом случае цифровой фильтр может быть выполнен либо для преобразования дискретных сигналов в реальном масштабе времени, либо для преобразования предварительно записанных сигналов.
В более узком смысле цифровой фильтр – это цифровая система, преобразовывающая спектры дискретных сигналов в соответствии с заданным алгоритмом.
В рекурсивном цифровом фильтре для формирования n-го отсчета используются предыдущие значения как входного, так и выходного отсчетов.

Коэффициенты  одновременно.
одновременно.
Системная функция данного рекурсивного цифрового фильтра:

Общее число элементов задержки равно 2m – это является недостатком данной структурной схемы. На практике обычно используются, так называемые канонические структурные схемы.
Характерной чертой рекурсивных цифровых фильтров является, в общем случае, бесконечность их импульсных характеристик. Такие цифровые фильтры называются БИХ-фильтры.
Цифровой фильтр называется устойчивым, если его импульсная характеристика удовлетворяет условию:
 ; из этого условия следует, что КИХ-фильтры всегда являются устойчивыми.
; из этого условия следует, что КИХ-фильтры всегда являются устойчивыми.
Условие устойчивости цифрового фильтра рекурсивного типа:
hn=ξ0 δh + ξ1p1n δn-1 +……+ ξn pNn δn-N
1. Вид передаточной функции:

2. Получение модуля частотной характеристики ЦФ

3.Получение импульсной и переходной характеристик ЦФ.
Импульсная характеристика фильтра-прототипа


| Переходная характеристика фильтра-прототипа: |




| Частотная характеристика фильтра-прототипа: |


| Дискретизация импульсной характеристики: |


5. Получение системной функции ЦФ

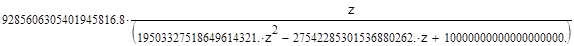



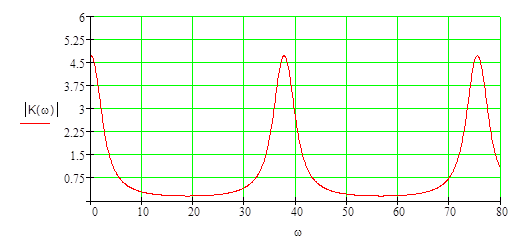
7.Получение импульсной и переходной характеристики ЦФ.









8.Проверка устойчивости ЦФ.
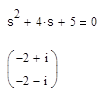

| Системная функция ЦФ в стандартной форме: |

Реализация:




Структурная схема:

Список использованной литературы
1. Ишемгужин А. И., Алтынбаева А. Р. Введение в теорию цифровых фильтров.-Уфа: УГНТУ.-2000.
2. Густав Деч. Руководство к практическому применению преобразования Лапласа и Z-преобразования.-М.: Наука.-1977.-288 с.
3. Гутников В. С. Фильтрация измерительных сигналов.-Л.: Энергоатомиздат, 1990.- 192 с.




