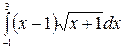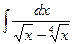аздел 1: векторная алгебра и аналитическая геометрия.
1. По координатам вершины пирамиды А1А2А3А4 найти:
1) длину ребра А1А2; 2) угол между ребрами А1А2 и А1А4; 3) угол между ребром А1А4 и гранью А1А2А3; 4) площадь грани А1А2А3; объем пирамиды; 5) уравнение прямой А1А2;
6) уравнение плоскости А1А2А3; 7) уравнение высоты, опущенной из вершины А4 на грань А1А2А3:
1. А1(4, 2, 5), А2(0, 7, 2), А3(0, 2, 7), А4(1, 5, 0)
2. А1(4, 4, 10), А2(4,10, 2), А3(2, 8, 4), А4(9, 6, 4)
3. А1(4, 6, 5), А2(9, 6, 4), А3(2,10,10), А4(7, 5, 9)
4. А1(3, 5, 4), А2(8, 7, 4), А3(5,10, 4), А4(4, 7, 8)
5. А1(10, 6, 6), А2(-2, 8, 2), А3(6, 8, 9), А4(7,10, 3)
6. А1(1, 8, 2), А2(5, 2, 6), А3(5, 7, 4), А4(4,10, 9)
7. А16, 6, 5), А2(4, 9, 5), А3(4, 6,11), А4(6, 9, 3)
8. А1(7, 2, 2), А2(5, 7, 7), А3(5, 3, 1), А4(2, 3, 7)
9. А1(8, 6, 4), А2(10, 5, 5), А3(5, 6, 8), А4(8,10, 7)
10. А1(7, 7, 3), А2(6, 5, 8), А3(3, 5, 8), А4(8, 4, 1)
II. Линейная алгебра
1) Заданы матрицы А= 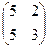 и В=
и В= 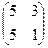 .Найдите произведение АВ
.Найдите произведение АВ
3) Заданы матрицы А=  и В=
и В=  .Найдите произведение АВ
.Найдите произведение АВ
4) Заданы матрицы А= 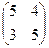 и В=
и В=  .Найдите произведение АВ
.Найдите произведение АВ 
5) Заданы матрицы А=  и В=
и В=  . Найдите произведение ВА
. Найдите произведение ВА
6) Заданы матрицы А= 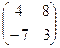 и В=
и В=  . Произведением ВА является…
. Произведением ВА является…
7) Заданы матрицы А=  и В=
и В=  .Произведением АВ является
.Произведением АВ является
8) Заданы матрицы А=  и В=
и В=  . Сумма 5А+4В
. Сумма 5А+4В  равна
равна
9) Заданы матрицы А=  и В=
и В=  . Сумма 4А
. Сумма 4А  +5В равна
+5В равна
10) Заданы матрицы А=  и В=
и В= 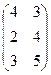 . Сумма 6А
. Сумма 6А  +2В равна
+2В равна
11) Заданы матрицы А=  и В=
и В=  . Сумма 2А+3В
. Сумма 2А+3В  равна
равна
12) Заданы матрицы А=  и В=
и В=  . Сумма 6А-3В
. Сумма 6А-3В  равна
равна
13) Заданы матрицы А= 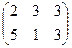 и В=
и В=  . Сумма 3А
. Сумма 3А  -5В равна
-5В равна
14) Заданы матрицы А=  и В=
и В=  . Сумма 2А -3В
. Сумма 2А -3В  равна
равна
15) Обратной к матрице  является матрица
является матрица
16) Обратной к матрице  является матрица
является матрица
17) Обратной к матрице  является матрица
является матрица
18) Обратной к матрице 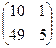 является матрица
является матрица
19) Определитель матрицы  равен
равен
20) Определитель матрицы  равен
равен
21) Определитель  равен…
равен…
22) Определитель  равен…
равен…
23) Определитель  равен…
равен…
8. Найдите произведение матриц ААТ:  .
.
9. Найдите произведение матриц АТА:.  .
.
1. Найдите произведение матриц:
10. 1) 

11. Найдите 3A + 2B - 4C, 
12. Найдите A – 12E, 
13. Решите матричное уравнение:  .
.
14. Решите матричное уравнение:  .
.
15. Решите матричное уравнение:  .
.
16. Решите матричное уравнение:  .
.
17. Найдите А–1, если  .
.
18. Найдите А–1, если  .
.
19. Вычислите определитель  .
.
20. Вычислите определитель 
21. Вычислите определитель 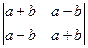 .
.
22. Вычислите определитель  .
.
23. Решите уравнение:  .
.
24. Решите уравнение:  .
.
25. Решите уравнение:  .
.
26. Вычислите определитель  .
.
27. Найдите ранг матрицы  .
.
28. Найти ранг матрицы 
29. Найти ранг матрицы 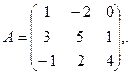
30. Найти ранг матрицы 
31. Найти ранг матрицы 
32. Решите систему линейных уравнений:  .
.
1. 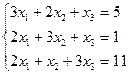
| 2. 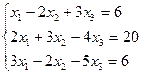
|
3. 
| 4. 
|
5. 
| 6. 
|
7. 
| 8. 
|
9. 
| 10. 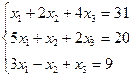
|
МАТЕМАТИЧЕСКИЙ АНАЛИЗ
I. Вычисление пределов функций.
1. Вычислить пределы, не используя правило Лопиталя:
А) 1)  2)
2)  3)
3)  4)
4)  5)
5)  6)
6)  7)
7)  8)
8)  9)
9)  10)
10)  11)
11)  12)
12) 
13)  14)
14)  15)
15) 
16)  17)
17)  18)
18) 
19)  20)
20)  21)
21) 
22)  23)
23)  24)
24) 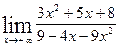
25)  26)
26) 
27)  28)
28) 
В) 1)  2)
2)  3)
3)  4)
4)  5)
5)  6)
6) 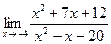 7)
7)  8)
8)  9)
9)  10)
10)  11)
11)  12)
12) 
13)  14)
14)  15)
15) 
16)  17)
17)  18)
18)  19)
19)  20)
20)  21)
21) 
22)  23)
23)  24)
24)  25)
25) 
С) 1)  2)
2)  3)
3)  4)
4) 
5)  6)
6)  7)
7) 
8)  9)
9)  10)
10)  11)
11) 
12)  13)
13) 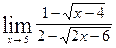 14)
14)  15)
15) 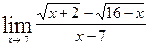
16) 
D) 1)_  2)
2)  3)
3)  4)
4)  5)
5) 
6) 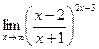 7)
7) 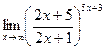 8)
8)  9)
9)  10)
10) 
E)1)  2)
2)  3)
3)  4)
4) 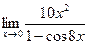 5)
5) 
6)  7)
7)  8)
8)  9)
9) 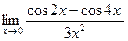 10)
10) 
11)  12)
12)  13)
13)  14)
14)  15)
15)  16)
16)  17)
17)  18)
18)  19)
19)  20)
20) 
G) Определить характер точек разрыва функции:
1) y=  ; 2) y=
; 2) y=  ; 3)y=
; 3)y=  ; 4) y=
; 4) y=  ; 5) y=
; 5) y=  ;
;
6) y = 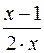 ; 7) y =
; 7) y =  ; 8) y =
; 8) y =  ; 9) y =
; 9) y =  ; 10) y =
; 10) y =  ;
;
11)  12)
12)  13)
13)  14)
14) 
15)  16)
16)  17)
17)  18)
18) 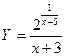
19)  20)
20)  21)
21)  22)
22) 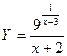 23)
23) 
II. Вычислить производные следующих функций:
А. 1.a) 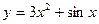 b)
b)  c)
c) 
2. a)  b)
b)  c)
c) 
3. a)  b)
b) 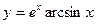 c)
c) 
4. a) 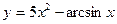 b)
b)  c)
c) 
5. a) 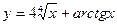 b)
b)  c)
c) 
6. a)  b)
b)  c)
c) 
7. a)  b)
b)  c)
c) 
8. a)  b)
b)  c)
c) 
9. a)  b)
b)  c)
c) 
10. a)  b)
b)  c)
c) 
В. 1)  2)
2)  3)
3) 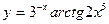 4)
4) 
5)  6)
6) 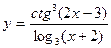 7)
7)  8)
8)  9)
9) 
10)  11)
11)  12)
12)  13)
13) 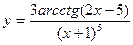
14)  15)
15) 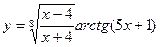 16)
16) 
17)  18)
18) 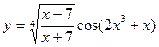 19)
19)  20)
20)  21)
21)  22)
22)  23)
23)  24)
24)  25)
25) 
26) 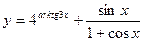 27)
27)  28)
28) 
29)  30)
30)  31)
31)  32)
32) 
33)  34)
34)  35)
35) 
С. Найти производную показательно-степенной функции
1)  2)
2) 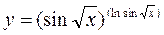 3)
3)  4)
4) 
5) 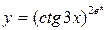 6)
6)  7)
7)  8)
8) 
9)  10)
10) 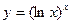 11)
11) 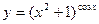 12)
12)  13)
13) 
D. Найти производную параметрически заданной функции:
1) x=t-sint, y=2-cost; 2) x=e-t, y=arcsint; 3) x=sint+cost, y=sin2t;
4) x=tg2t, y=cos2t; 5) x=sint, y=ln(cost); 6) x=etsint, y=t+sint
7)  8)
8)  9)
9)  10)
10) 
11) 
E. Найти производную неявно заданной функции у/х
1) x+cos(xy)=5; 2) 2xy-3y2x+x=9; 3) x-2ycosy2=0; 4) xex-y-sinx+10=0;
 ; y ln x+x ln y=7; 5xy+cosx+siny=0
; y ln x+x ln y=7; 5xy+cosx+siny=0
5) tg y=4y-5x 6) y=7x-ctgx 7) yx-6=cosx 8) y=ey+4x 9) 4sin2(x+y)=x
10) y2+x2=siny 11) y2=x+cosy 12) lny-y/x=7 13) xy2-y3=4x-5 14) x+arctgy=y
G. Найти промежутки монотонности функции, точки экстремума
1)  2)
2)  3)
3)  4)
4)  5)
5)  6)
6)  7) y =ln (1-x2)
7) y =ln (1-x2)
8)  9)
9)  10)
10)  11)
11)  12)
12) 
H. Найти промежутки выпуклости-вогнутости, точки перегиба
1)  2)
2)  3)
3)  4)
4)  5)
5) 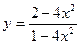
6)  7)
7)  8)
8)  9)
9)  10)
10) 
К. Найти асимптоты графиков функций
1)  2)
2)  3)
3)  4)
4) 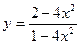 5) y=
5) y=  6)
6)  7) y=xe-x
7) y=xe-x
8)  9)
9)  10)
10)  11)
11)  12)
12) 
13) 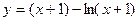 14)
14)  15)
15) 
Раздел 2: Интегральное исчисление
А. Непосредственное интегрирование













Б. Метод подведения под знак дифференциала









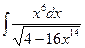









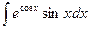



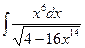
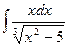


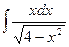
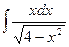


 .
.








 .; а)
.; а)  ;;
;;  ;;)
;;)  ;;
;;  ;;
;;  ;;
;;  ;;
;;  ;;.; а)
;;.; а)  ;;
;;  ;;
;;  ;
;
В. Метод интегрирования по частям

















 (x+12)cos
(x+12)cos  dx
dx 


 .
.


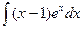





 .
.
Г. Метод неопределенных коэффициентов



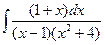

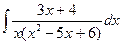


Д. Метод замены переменной


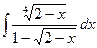








 .
.