еорема. Множество подмножеств данного множества по мощности больше самого множества.

Теорема утверждает, что на основе любого множества (конечного или бесконечного) можно построить множество большей мощности и, следовательно, классов эквивалентности бесконечных множеств неограниченное количество.

 

9. Кардинальные числа. Эквивалентность конечных множеств – основа комбинаторики (Л).

КАРДИНАЛЬНОЕ ЧИСЛО —важное понятие абстрактной теории множеств. Кардинальное число характеризует множество с точки зрения запаса его элементов — мощности множества (это обобщение понятия количества (числа элементов множества), которое имеет смысл для всех множеств, включая бесконечные). Кардинальное число является обобщением понятия количественного числа на бесконечные множества. Интересным при таком обобщении является то обстоятельство, что одно и то же бесконечное множество можно по-разному упорядочить и в связи с этим кардинальные числа резко отличается от трансфинитных чисел (обобщение понятия порядковых чисел для бесконечных множеств). Для конечных множеств кардинальное число совпадает с трансфинитным числом и равно количеству элементов множества.

Два множества А и В,между которыми можно установить взаимно однозначное соответствие,называются эквивалентными.Между элементами х и у множества А установлено отношение эквивалентности,если оно удовлетворяет свойствам:

1)каждый элемент множества А (х) эквивалентен самому себе.(рефлективность)

2)если элемент х эквив.У,то у экв.х (симметрия,взаимность)

3)если элемент х эквив.у,то у экв. Z(транзитивность)

Отношение эквивалентности тесно связано с разделением множеств на классы.

 

Конечное множество — множество, количество элементов которого конечно, то есть, существует неотрицательное целое число k, равное количеству элементов этого множества. В противном случае множество называется бесконечным. Например,

 

\{2,4,6,8,10\}\,\!

конечное множество из пяти элементов. Число элементов конечного множества это натуральное число и называется мощностью множества.

 

Что такое эквивалентные множества?

 

 

Если множества конечные, то сравнить их по количеству элементов просто, достаточно посчитать элементы в каждом множестве и сравнить полученные значения.

 

Однако если множества даже конечные, но в них слишком много элементов, то подобный подход не слишком эффективен. Есть другой способ. Надо поставить в соответствие элементам одного множества элементы другого. Если при этом каждый найдет себе пару, то эти множества равны по количеству элементов. Если это окажется не так, то большим будет то множество, где останутся элементы, которым не были сопоставлены элементы из другого множества.

 

Например, если раздать тетради по математике ученикам класса, то можно сразу узнать, все ли в классе или кто-то отсутствует.

 

Подобный метод сопоставления подходит не только для конечных множеств, но и для бесконечных.

 

Особенностью эквивалентных множеств является то, что каждому элементу из одного множества сопоставляется только один элемент из другого множества. При этом нет ситуаций, когда одному элементу из одного множества, сопоставляется два или больше из другого.

 

Примером эквивалентных множеств может служить множество натуральных чисел, которым сопоставляется множество отрицательных целых чисел.

 

В случае эквивалентных множеств говорят о взаимно-однозначном соответствии между ними. Эквивалентные множества имеют одинаковую мощность.

10. Множество N натуральных чисел. Счетные множества. Теоремы о счетных множествах.

Первоначальный класс эквивалентности для бесконечных множеств порождается множеством натуральных чисел.

Классом эквивалентности А_х элемента хÎА называется множество элементов из А эквивалентных х:А_х = {y:y~x, yÎA}. Различные классы не пересекаются, и каждый элемент множества входит хотябы в один из классов.

Множество А называется счетным, если его можно поставить во взаимно однозначное отношение с множеством натуральных чисел.

Каждый элемент а множества А имеет свой индивидуальный номер n и его будем записывать в виде а_n·. Само множество А можно записать в виде последовательности перечислением элементов: А = {a₁,a₂,a₃,…,a_n,…}. Понятное, что если множество описывается подобным образом, то оно счетное.

Свойства счетных множеств описываются в теоремах:

Теорема 1. Любое подмножество счетного множества либо конечное, либо счетное множество.

Теорема 2. Если счетному множеству добавить один элемент, то получим счетное множество.

Теорема 3. Объединение счетного числа конечных или счетных множеств будет счетным множеством.

Теорема 4. Любое бесконечно множество содержит счетное подмножество.

Теорема 5. Объединение счетного и произвольного бесконечного множества не изменяет класса эквивалентности последнего.

Теорема 6. Из произвольного бесконечного множества можно вычесть счетное подмножество таким образом, что оставшееся множество будет эквивалентно исходному множеству.

Приведенные формулировки теорем для класса счетных множеств, показывают, что счетные множества, как бесконечные, обладают новыми качествами по сравнению с конечными.

11. Множества мощности континуум. Теорема Кантора о несчетности множества точек отрезка [0,1].

Множества эквивалентные множеству чисел (или точек) отрезка (0,1) называются множествами типа континуум.

Множества типа континуум обладают еще больше экспансией по сравнению со счетными множествами. Назовем множества, входящие в этот класс эквивалентности: произвольный отрезок или интервал, вся числовая прямая, точки плоскости, трехмерного и n-го пространства, и, вообще, сумма счетного числа множеств мощности континуум есть множество мощности континуум. Теорема Кантора о том, что множество подмножеств данного множества по мощности больше самого множества, не позволяет останавливаться на множествах типа континуум и множетсво подмножеств интревала (0,1) образует следующий более мощный класс эквивалентности. Элементами множества этого класса будут функции заданные на (0,1). Данная теорема рисует бесконечную систему классов эквивалентности, на которую разбивается вся совокупность множеств.

Теорема Кантора о несчетности множества точек отрезка (0,1) (0<x<1)

Множество действительных чисел интервала [0,1] несчетно.

Доказательство проведем от противного. Предположим, что множество чисел интревала (0,1) счетное множество и может быть представлено в виде последовательности чисел х₁,х₂,х₃,…,х_n,… Каждое из чисел х_n представляет собой правильную дробь и записывается в виде бесконечной десятичной дроби: х_n = 0, a_1n, a_2n, a_3n,…,a_kn… Величины а_kn представляют собой соответствующие десятичные разряды числа х_n, т.е. равны одному из целых чисел от 0 до 9. Одна и таже дробь может быть представлена в виде бесконечной десятичной дроби двояким образом. Например, дробь 0,1 и дробь 0,0(9) это одно и тоже действительное число, записанное разными десятичными дробями. Исключим дроби с девяткой в периоде, и тогда представление числа станет однозначным. При этом два числа х_n и х_m будут равны друг другу только в том случае, когда все разряды одного числа совпадут с разрядами второго числа: a_kn = a_km , (k=1,2,3,…).

Построим число у, которое принадлежит отрезку (0,1) и не равно ни одному из чисел х₁,х₂,х₃,…,х_n,… Это будет означать, что наше предположение о счетности множества (0,1) неверно и теорема будет доказана. Число у представим также в виде десятичной дроби у= 0, b₁,b_2,b₃,…,b_n…, каждый разряд которого b_n выберем отличным от разряда а_nn числа х_n·. такой выбор разрядов числа у возможен многими способами,например, если а_nn = 2, b_n полагаем равным 3, если a_nn ¹ 3, то b_n = 3. ВИдно, что построение такие образом числу у отрезку (0,1) и не совпадает ни с одним из чисел х₁,х₂,х₃,…,х_n,…, т.к. с каждым из них оно отличается хотя бы в разряде. Теорема доказана.

12. Построение множества большей мощности, чем исходное. Теорема Кантора-Бернштейна (без доказательства) (Л).

Теорема. Множество подмножеств данного множества по мощности больше самого множества.

Теорема утверждает, что на основе любого множества (конечного или бесконечного) можно построить множество большей мощности и, следовательно, классов эквивалентности бесконечных множеств неограниченное количество.

1.Любые два множества, между элементами которых может быть установлено взаимно однозначное соответствие содержат одинаковое количество элементов (имеют одинаковую мощность)

2.Обратно: множества, равные по мощности, должны допускать такое взаимно однозначное соответствие.

3.Часть множества не превосходит полного множества по мощности (то есть по количеству элементов).

13. Общая структура бесконечности. Числовая прямая и ее конструктивное устройство.

Бесконечность — категория человеческого мышления, используемая для характеристики безграничных, беспредельных, неисчерпаемых предметов и явлений, для которых невозможно указание границ или количественной меры. Используется в противоположность конечному, исчисляемому, имеющему предел.

Одним из основных источников ранних представлений о бесконечности были натуральные числа и потенциальная бесконечность натурального ряда. Одним из первых нетривиальных результатов о бесконечности в теории чисел считается доказательство от противного бесконечности множества простых чисел в «Началах» Евклида: предполагая конечность множества простых чисел, прибавляя к их произведению единицу вновь получается простое число. => Единичное не изменяет бесконечное! Теоретико-числовое суждение о бесконечности представляет парадокс Галилея: каждому числу может быть сопоставлен его квадрат, то есть, квадратов не меньше, чем всех чисел, но при этом не из каждого числа можно извлечь корень, то есть, квадраты — только часть множества всех чисел.

Основной вклад в представление о бесконечности в математике внесён теорией множеств: идея актуальной бесконечности и разных сортов бесконечности занимают существенную часть этой теории.

Для измерения разных видов бесконечности в теории множеств вводится понятие мощности (кардинального числа), совпадающее с количеством элементов для конечных множеств, а для бесконечных множеств задействующее принцип биекции(взаимно-однозначности): если между множествами возможно установить взаимно-однозначное соответствие, то они равномощны. (Взаимно-однозначные отображения между множествами возможны тогда и только тогда, когда эти мн-ва имеют одинаковое кол-во элементов.) Так, оказывается, что множество натуральных чисел равномощно множествам целых чисел (), чётных натуральных чисел, всех рациональных чисел (), а отрезок числовой прямой (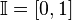, континуум) оказывается во взаимно-однозначном соответствии со всей числовой прямой (), а также с -мерным евклидовым пространством () (Теорема Кантора о несчетности чисел отрезка (0,1). М={0<x<1} эквивалентно всей числовой прямой. Они из одного класса типа континуум. Все 3хмерное пространство эквивалентно отрезку (0,1). Любое N-мерное пространство – континуум.).

 

Т.е. между двумя рациональными числами всегда бесконечно много рациональных.

Множество рациональных чисел на числовой прямой счетно.

 

14. Натуральные, целые, рациональные и иррациональные числа и их взаимное расположение на числовой прямой. Четвертая проблема Гильберта и ее решение (Л).

Натуральные числа – это числа, получаемые при естественном счёте предметов, а вернее при их нумерации («первый», «второй», «третий»...). Множество натуральных чисел обозначается латинской буквой N (можно запомнить, опираясь на английское слово natural). Можно сказать, что N ={1,2,3,....}

Целые числа – это числа из множества {0, 1, -1, 2, -2,....}. Это множество состоит из трех частей – натуральные числа, отрицательные целые числа (противоположные натуральным числам) и число 0 (нуль). Целые числа обозначаются латинской буквой Z. Можно сказать, что Z ={1,2,3,....}.

Рациональные числа – это числа, представимые в виде дроби, где m — целое число, а n — натуральное число. Для обозначения рациональных чисел используется латинская буква Q. Все натуральные и целые числа – рациональные.

Иррациональные числа - это бесконечные непериодические десятичные дроби.

Действительные числа – рациональные + иррациональные

координатная прямая – это прямая, на которой выбрано начало отсчета, указан единичный отрезок и задано направление. Нам известно, что на данной прямой линии лежит бесконечно много точек. Не является исключением и координатная прямая – она также содержит бесконечно много точек. Между точками координатной прямой и действительными числами существует очень важная связь, которую называют взаимно однозначным соответствием. Эта связь выражается следующим утверждением: каждой точке координатной прямой соответствует единственное действительное число, а каждому действительному числу соответствует единственная точка на координатной прямой. Вот почему координатную прямую очень часто называют числовой прямой. Точкам, лежащим правее начала отсчета на числовой прямой, соответствуют положительные числа, а точкам, лежащим левее начала отсчета, - отрицательные.

15. Комплексные числа и действия над ними. Комплексная плоскость. Тригонометрическая форма комплексных чисел.

Возникновение комплексных чисел связано с решением алгебраических уравнений. В некоторых случаях решение уравнения представлялось в двух видах: являлось действительным числом и имело вид формул с корнями из отрицательных чисел.

Комплексным числом z называется выражение x=a+bi, где a,b – действительные числа, а символ i (или j в некоторых трудах) – мнимая единица.

Число а называется действительной частью мнимого числа z и обозначается Re z=a, число b – мнимой частью z и обозначается Im z=b, т.е. z=Rez+iImz.

Числами введенные объекты z становятся лишь тогда, когда для них будут определены арифметические операции (сложение, вычитание, умножение, деление).

Арифметические операции над комплексными числами:

Пусть заданы два комплексных числа z₁=x₁ + iy₁, z₂ = x₂+ iy₂.

1) Сложение и вычитание z₁±z₂ = (x₁±x₂) + i(y₁±y₂);

2) Умножение z₁z₂ = (x₁x₂ – y₁y₂) +i(x₁y₂ + x₂y₁);

Умножение образуется раскрытием скобок в выражении

(x₁ + iy₁)(x₂ +iy₂) и заменой i² на минус единицу (-1).

3) Деление z₁/z = x₁x₂+y₁y₂/ x₂²+y₂² +i x₂y₁-x₁y₂/x₂²y₂²

Деление основано на свойстве дробей не изменяться при умножении числителя и знаменателя на одно и тоже число. Достаточно дробь умножить на дробь , где число z₂*=x₂ –iy₂ называется комплексно сопряженным числу z=x+iy. При этом числитель и знаменатель дроби умножаются соответсвенно на число z₂* комплексно сопряженное знаменателю.

Свойства комплексного сопряжения:

1) если z=z*, то z – действительное число;

2) (z±z₂)* = z₁*±z₂*;

3) (z₁z₂) = z₁*z₂*

4) (

(скобки под звездочкой, z₁ , z₂ – со звездочкой)

Модуль комплексного числа:

Число 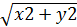называется модулем |z| комплексного числа z: |z|= Очевидно, |z| =

Свойство модулей комплексных чисел:

1)|z₁z₂| = |z₁| * |z₂|;

2) |z| = |z*|;

3) |z₁/z₂| = |z₁| / |z₂|.

 

Комплексное число z=x+iy определяется упорядоченной парой чисел (х,у), что соответствует точке P(x,y) на плоскости в декартовой системе координат.

Взаимно однозначное соответствие комплексных чисел z=x+iy и точек P(x,y) плоскости образуют комплексную плоскость и позволяет изображать комплексные числа и их множества в виде геометрических объектов плоскости.

Так, например, комплексно сопряженное число z*=x-iy изображается симметричной точкой P*(x, -y) относительно оси Ох, а модуль |z| числа z, согласно теореме Пифагора, есть длина отрезка ОР (гипотенуза прямоугольного треугольника).

Угол j, образованный осью абсцисс ОХ и отрезком ОР (направление против часовой стрелки является положительным) называется аргументом числа z и обозначается arg z.

Очевидно, что одному комплексному числу соответствует бесконечное множество аргументов, отличающихся друг от друга на кратное число полных оборотов 2pk, kÎz. Деление угла j на 2p и получение остатка аргумент z всегда можно произвести к значениям от 0 до 2p (0£ arg z <2p). Такая процедура называется приведением аргумента.

Эквивалентная возможность геометрической интерпритации комплексных чисел состоит в отождествлении числа z с вектором`OP.

Корординаты х и у у вектора можно вычислить через параметры комплексного числа:

x = Re z = r cosj = |z| cos arg z;

y = Imz = r cosj = |z| cos arg z, где r = |z|.

Представляя полученные значения х и у в исходное определение комплексного числа z= x+iy, получим запись этого числа в тригонометрической форме:

z = x + iy = r cosj +I r sinj = |z| (cos arg z + I sin arg z)

формула умножения: arg (z₁z₂) = arg z₁ + arg z₂

формула деления:

(квадратики – это j)., где r₁ = |z₁|, r₂ = |z₂|, j₁ = arg z₁, j₂ = arg z₂.

 

16.Формула Муавра.

Формула Муавра – это формула, содержащая правило для возведения в степень n комплексного числа, представленного в тригонометрической форме

z = ρ (cos φ + i sin φ);

согласно этой формуле, модуль ρ комплексного числа возводится в эту степень, а аргумент φ умножается на показатель степени

zⁿ = [ρ (cos φ + i sin φ)] ⁿ = ρ ⁿ (cos n φ + i sin n φ).

Формула Муавра была найдена А. Муавром в 1707; современная её запись предложена Л. Эйлером в 1748.

Формула Муавра может быть легко использована для выражения cos n φ и sin n φ через степени cos φ и sin φ; положив в формуле Муавра ρ = 1 и приравнивая отдельно действительные и мнимые части, получим

cos n φ = cosⁿ φ - C_n² cos^n-2 φ sin² φ + C_n⁴ cos^n-4 φ sin⁴ φ -...,

sin n φ = C_n¹ cos^n-1 φ sin φ - C_n³ cos^n-3 φ sin³ φ +...,

где C_n^m = n!/ m!(n - m)! — биномиальные коэффициенты (см. бином Ньютона). Обращение к формуле Муавра приводит к формуле для извлечения корня из комплексного числа.

17.Комбинаторика и ее задачи. Общие правила комбинаторики (правило суммы и правило произведения). Формула включений и исключений.

Комбинаторика занимается изучением различных комбинаций, обусловленных теми или иными ограничениями, которые можно составить из заданного конечного набора элементов. Исходными элементами, из которых набираются комбинации, могут быть: буквы, пробелы, знаки препинания, числа и иные объекты.

В основе всех задач комбинаторики лежит конечный набор (или несколько конечных наборов) n элементов: а1, а2,…,аn, из которых составляется комбинация длины m.

Типы комбинаторных задач:

1) если елементы в базовом наборе все различные и имеются в единственном экземпляре, то говорят о комбинаторике без повторений;

2) если элементы в составляющей комбинации могут повторяться, то говорят о комбинаторике с повторениями.

Решение этих типов задач осуществляется на основе общих принципов комбинаторики (принципов суммы и произведения, формулы включений и исключений).

Принцип суммы состоит в том, что общее количество комбинаций равно сумме числа комбинаций в каждом классе.

Принцип произведения указывает, что выбор пары объектов (a_k, b_l), где a_k из набора {a₁,a₂,…a_m}; b_l из набора {b1,b2,…bn}, можно осуществить mn способами.

Формула включений и исключений применяется в задачах, в которых некоторые элементы исходного множества (сотрудники научного института) обладают одним или несколькими качеставами (знают иностранные языки). Требуется определить количество объектов, не обладающих ни одним качеством (не знаю ни одного языка). Из общего числа сотрудников необходимо вычесть обладающих хотя бы одним качеством и прибавить обладающих двумя качествами. Для определения числа элементов, не обладающим ни одним качеством необходимо из общего количества элементов вычитать тех, которые обладают нечетным количеством качеств, и прибавлять тех, которые обладают четным количеством качеств. Образующая процедура расчета назватся формулой включений и иключений.

 

18. Комбинаторика без повторений элементов. Размещения, перестановки и сочетания без повторений (Л).

Правила комбинаторики применяются для расчета количества комбинаций из предлагаемого конечного набора элементов. Рассмотрим задачи, в которых исходные элементы все различны и могут встречаться только один раз. Такие задачи составляют раздел комбинаторики без повторений элементов. В зависимости от состава, порядка количества используемых в комбинации элементов, различают размещения, сочетания и перестановки.

В комбинаторике часто используют произведение натуральных чисел от единицы до n. Кратко обозначают n!=1*2*…*n

Размещениями из n элементов по m называются комбинации длины m (m£n), отличающиеся друг от друга порядком или составом элементов.

(обозначение А^m_n - А из n по m).

 

формула: А^m_n =

Пример: Сколькими способами можно составить комбинацию из трех букв слова камзол?

Решение: А³₆=6*5*4=120

 

Перестановками из n элементов P_n называют размещения из n элементов по n, т.е. P_n = A^m_n = n!

Пример: Сколькими способами можно переставить буквы в слове столица?

Решение: P₇ = 7! = 1*2*3*4*5*6*7 = …

 

Сочетаниями из n элементов по m называются комбинации длины m (m£n), отличающиеся друг от друга только составом элементов.

(обозначение С^m_n – C из n по m).

формула: A^m_n = P_mC^m_n

C^m_n =

Пример: сколькими способами можно выбрать две буквы из букв слова родина?

Решение: C^m_n =

19. Комбинаторика с повторениями элементов. Размещения, перестановки и сочетания с повторениями.

Комбинаторика с повторениями элементов. Элементы комбинации в этих задачах могут повторяться. Исходный набор не конкретные объекты, а типы элементов и количество одинаковых элементов (типов) в комбинациях определяется только условиями задачи.

Размещение с повторениями `A^m_n из n типов элементов по m элементов называются комбинации, отличающиеся друг от друга или типом элементов или их порядком в комбинации.

Формула А^m_n = n^m

Пример: сколькими различными способами можно составить комбинаций длины 8 из двух различных типов чисел «0» и «1»?

Решение: Число типов элементов равно 2 (n=2), а длина m составляемых комбинаций – 8 (м=8), следовательно, `А⁸₂ = 2⁸=256

Перестановки с повторениями обозначаются P(3,2,2).

Например, при рассмотрении слова колокол необходимо указать, что буква «о» встречается 3 раза, буква «к» - 2 раза, буква «л» - 2 раза. Общее количество букв в перестановках не изменяется и равно сумме всех букв в слове: 7=3+2+2

Формула: P(k₁,k₂,…,k_m) =

«колокол» = P(3,2,2,) =

Сочетания с повторениями называют комбинации из m предметов n типов, отличающихся составом предметов (обозначаются `С^m_n). Комбинации должны отличаться друг от друга хотя бы одним предметов.

Способ подсчета общего количества С^m_n таких комбинаций основан на специальном кодировании каждой комбинации двоичным кодом. Кодировать будем следующим образом: каждому типу припишем такое количество единиц, сколько предметов данного типа входит в комбинацию, а предметы различного типа отделим друг от друга нулями. (см. Тетрадь). При этом общее количество единиц в коде соответствует количеству m предметов в комбинации, а число разделяющих нулей равно числу необъодимых границ (n-1). Т.об. образуется взаимно однозначное соответствие между сочетаниями с повторениями элементов и комбинациями в виде двоичных кодов и, следовательно, их общее количество одинаково. Количество различных двоичных кодов с фиксированным числом единиц (m – штук) и нулей ((n-1) штук) подсчитывается по формуле перестановок с повторениями P(n-1,m). Таким образом, общее число `C^m_n =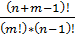

Пример: Сколько различных комбинаций можно составить из 5 букв типа а б в, отличающихся друг от друга только составом?

Решение: `5⁵₃ = P(3-1,5) =

20. Свойства сочетаний. Бином Ньютона. (Л).

 

Сочетаниями из n по m называют комбинации длины m(m<=n), отличающиеся друг от друга только составом элементов. Обозначаются сочетания C^m_n (читаются C из n по m)

Свойства сочетаний:

1. C^k_n = C^n-k_n Чтобы выбрать k элементов из множества в n элементов, можно указать те из них, которые останутся, не будут выбраны. Если мы выбираем k элементов, то остается Поэтому число выборок по k элементов (из n) равно числу выборок по элементов.

2. C^k_n = C^k-1_n-1 + C^k_n-1 Подсчитаем двумя способами общее возможное число выборок из множества, содержащего n элементов (число всех подмножеств n -элементного множества).
С одной стороны это число равно 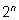– для каждого элемента есть две возможности: попасть или не попасть в выбираемое подмножество, причем для каждого элемента эти возможности выбираются независимо друг от друга.
Это же число можно получить иначе – сначала зафиксировать число k элементов в подмножестве. Получим число а затем сложим по всем k, чтобы найти общее число вариантов.

3. C⁰_n + C¹_n +… + Cⁿ_n = 2ⁿ Представим себе, что к n элементам данного множества мы добавили еще один, и из полученного множества хотим выбрать подмножество из элемента. По определению это число равно Все эти выборки мы разобьем на два сорта – те, которые содержат один добавленный элемент, и те, которые его не содержат. Первых будет штук (один элемент уже взят, а из остальных надо взять еще k), а вторых – 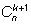(все элементов берутся из исходного множества). Тем самым
Это равенство лежит в основе построения так называемого треугольника Паскаля, позволяющего быстро вычислять числа сочетаний для небольших значений n.

 

Бином Ньютона – особая формула, описывающая разложение сложения двух чисел по алгебраическим методам в любой степени.

 

 

(x+a)n = C⁰_nxⁿ + C¹_nx^n-1a + C²_nx^n-2a² +…+Cⁿ_naⁿ - это из его лекций