итуационная (практическая) задача № 1
При исследовании некоторого непрерывного признака ξ экспериментатор предположил, что этот признак подчиняется закону распределения с плотностью

§ При каком значении С экспериментатор будет прав? Построить график плотности распределения.
§ Найти функцию распределения с.в. ξ и построить её график.
§ Вычислить математическое ожидание (среднее значение) Мξ, дисперсию Dξ и среднее квадратическое (стандартное) отклонение рассматриваемой случайной величины
Во сколько раз число опытов, в которых экспериментатор будет получать результат больше среднего значения, превышает число опытов, в которых результат будет меньше среднего значения?
Решение:
Найдем C исходя из свойства плотности распределения:
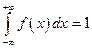
Тогда:

Построим график плотности распределения

Найдем функцию распределения
а) если x<0, то F(x)=0, т.к. значений, меньших 0, случайная величина не принимает.
б) если 0£x<2, то

в) если 2£x<5, то

г) если x>5, то
 в силу свойства плотности распределения
в силу свойства плотности распределения
Тогда функция распределения будет иметь следующий вид:
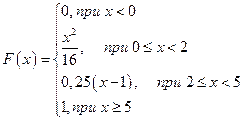
Построим ее график:

Найдем математическое ожидание и дисперсию. Математическое ожидание вычисляется по формуле
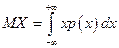
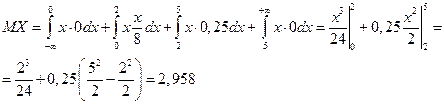
Дисперсия вычисляется по формуле:
 , где
, где 
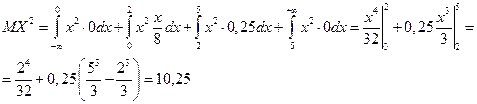
Тогда дисперсия будет равна:
DX=10,25-2,9582=1,498
Среднее квадратическое отклонение равно: 
Найдем требуемую вероятность:
Р(X<MX)=Р(X<1,224)=F(1,224)= 
Р(X³MX)=1–Р(X<MX)=1–0,0936=0,9064
Тогда число опытов, в которых результат будет больше среднего значения, превосходит число опытов, в которых результат будет меньше среднего значения, в 0,9064/0,0936=9,7 раза.
итуационная (практическая) задача № 2
В отделе 7 сотрудников, из которых 5 женщин и 2 мужчин. Среди них по жребию разыгрывают 3 ноутбука. Составить ряд и функцию распределения числа мужчин, выигравших ноутбук, и представить их графически.
Решение:
Определим возможные значения случайной величины Х и их вероятности:
Х=0: 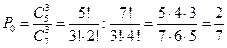
Х=1: 
Х=2: 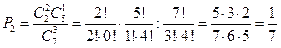
Запишем ряд распределения
| x | |||
| p | 
| 
| 
|
Изобразим ряд распределения графически в виде полигона

Составим функцию распределения:

Построим график функции распределения


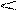

Тестовые задания
Необходимо из предложенных вариантов ответа на вопрос теста выбрать единственно верный, по Вашему мнению.
1. Из 9 сотрудников отдела коммерческого банка, среди которых пятеро мужчин, а остальные женщины, случайным образом формируется комиссия из трех человек. Найти вероятность того, что в комиссии хотя бы один мужчина.
А. 0,9524
Б. 0,4762
В. 0,0476
Г. 0,0476
Решение:
Перейдем к противоположному событию, т.е. найдем вероятность того, что в комиссии не будет мужчин. Общее количество равновозможных исходов равно количеству способов выбора 3 человек из 9, т.е.  . Чтобы в комиссии не было мужчин, в ней должны быть все женщины, поэтому количество благоприятных исходов равно
. Чтобы в комиссии не было мужчин, в ней должны быть все женщины, поэтому количество благоприятных исходов равно  . Тогда вероятность будет равна:
. Тогда вероятность будет равна:

Тогда вероятность того, что в комиссии будет хотя бы один мужчина, будет равна:

Ответ: А.
2. На стройку от трех разных поставщиков должны поступить три партии материалов. Известно, что первый поставщик доставляет материалы своевременно в среднем в 84% всех случаев, второй – в 85%, третий – в 80%. Найти вероятность того, что из трех партий на стройку будет доставлена своевременно ровно одна.
А. 0,5712
Б. 0,3524
В. 0,0716
Г. 0,0048
Решение:
Пусть:
Событие А – первый поставщик доставит товары своевременно
Событие В – второй поставщик доставит товары своевременно
Событие С – третий поставщик доставит товары своевременно
Тогда
Событие  – первый поставщик не доставит товары своевременно
– первый поставщик не доставит товары своевременно
Событие  – второй поставщик не доставит товары своевременно
– второй поставщик не доставит товары своевременно
Событие  – третий поставщик не доставит товары своевременно
– третий поставщик не доставит товары своевременно
По условию задачи:
Р(А)=0,84 ↔ Р( )=1-0,84=0,16;
)=1-0,84=0,16;
Р(В)=0,85 ↔ Р( )=1-0,85=0,15;
)=1-0,85=0,15;
Р(С)=0,8 ↔ Р( )=1-0,8=0,2
)=1-0,8=0,2
Пусть событие F – из трех партий только одна будет доставлена своевременно, тогда
F = A×  ×
×  +
+  ×B×
×B×  +
+  ×
×  ×C
×C
P(F)=P(A)×P( )×P(
)×P( )+P(
)+P( )×P(B)×P(
)×P(B)×P( )+P(
)+P( )×P(
)×P( )×P(C)=0,84×0,15×0,2+0,16×0,85×0,2+
)×P(C)=0,84×0,15×0,2+0,16×0,85×0,2+
+0,16×0,15×0,8=0,0716
Ответ: В.
3. На складе находятся одинаковые изделия, изготовленные тремя заводами: первым заводом произведено 30% всех изделий, вторым – 20%, а остальные изделия с третьего завода. Известно, что из каждой сотни изделий удовлетворяют стандарту в среднем 88 изделий, изготовленных на первом заводе, 82 – на втором, 78 – на третьем. Для контроля качества наудачу берется одно изделие. Найти вероятность того, что это изделие окажется стандартным.
А. 0,818
Б. 0,264
В. 0,164
Г. 0,39
Решение:
Рассмотрим гипотезы:
H1 – изделие оказалось с первого завода
H2 – изделие оказалось со второго завода
H3 – изделие оказалось с третьего завода
и событие
F – изделие оказалось стандартным.
Тогда
| P(H1)= | 0,3 | P(F/H1)= | 0,88 |
| P(H2)= | 0,2 | P(F/H2)= | 0,82 |
| P(H3)= | 0,5 | P(F/H3)= | 0,78 |
Гипотезы Hi образуют полную группу, поэтому по формуле полной вероятности получим:
 =0,3×0,88+0,2×0,82+0,5×0,78=0,818
=0,3×0,88+0,2×0,82+0,5×0,78=0,818
Ответ: А.
4. Имеется коробка с 3 изделиями одного образца, причем среди них с одинаковой вероятностью возможно любое количество бракованных изделий (от 0 до 3). Из коробки наудачу выбирается одновременно два изделия, среди которых оказалось одно бракованное. Найти вероятность того, что изначально в коробке было 2 бракованных изделия.
А. 0,5
Б. 0,3333
В. 0,6667
Г. 0,25
Решение:
Рассмотрим гипотезы:
H1 – в коробке нет бракованных изделий
H2 – в коробке 1 бракованное изделие
H3 – в коробке 2 бракованных изделия
H4 – в коробке 3 бракованных изделия
и событие
F – одно из двух извлеченных изделий бракованное
Тогда
P(H1)= 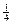
| P(F/H1)=0 |
P(H2)= 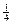
| P(F/H2)= 
|
P(H3)= 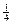
| P(F/H3)= 
|
P(H4)= 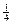
| P(F/H4)=0 |
События Hi образуют полную группу, поэтому по формуле полной вероятности получим:
 =
= 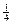 (0+
(0+  +
+  +0)=
+0)=  =0,3333
=0,3333
Т.к. одно из двух извлеченных изделий оказалось бракованным, т.е. событие F произошло, то вероятности гипотез определим по формуле Байеса:


Ответ: А.
5. В результате проверки качества приготовленных для посева семян огурца установлено, что в среднем 86% семян всхожи. Какова вероятность, что из посеянных пяти семян взойдут ровно три?
А. 0,1247
Б. 0,8753
В. 0,0203
Г. 0,9797
Решение:
Значение n<10, поэтому для расчетов воспользуемся формулой Бернулли:

q =1- p =1-0,86=0,14
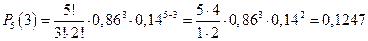
Ответ: А.
6. При опускании одной монеты автомат срабатывает неправильно в среднем в 12 случаях из ста. Какова вероятность того, что при опускании 5 монет автомат сработает правильно хотя бы три раза?
А. 0,9857
Б. 0,0143
В. 0,999
Г. 0,001
Решение:
Значение n<10, поэтому для расчетов воспользуемся формулой Бернулли:

p =1- q =1-0,12=0,88
P(хотя бы 3)=P5(3)+P5(4)+P5(5)


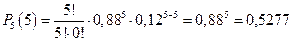
Тогда
P(хотя бы 3)=0,0981+0,3598+0,5277=0,9856
Ответ: А.
7. Согласно статистическим данным в городе N в среднем 22% открывающихся новых предприятий прекращают свою деятельность в течение года. Какова вероятность, что из двухсот наугад выбранных новых предприятий к концу года деятельности останется не менее 40, но не более 50 предприятий?
А. 0,5998
Б. 0,2473
В. 0,8471
Г. 0,3471
Решение:
n =200 q =0,22 p =1- q =1-0,22=0,78
Значение n =200 достаточно велико, поэтому для расчетов воспользуемся интегральной формулой Лапласа:
Pn(k1;k2)»Ф(x2)-Ф(x1), где 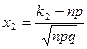 и
и  , а Ф(x) - интегральная функция Лапласа
, а Ф(x) - интегральная функция Лапласа
 ,
, 
По таблице значений функции Ф(x) находим, что Ф(-19,8)=-Ф(19,8)=-0,5, а
Ф(-18,1)=-Ф(18,1)=-0,5, Þ P200(40;50)»-0,5+0,5@0
Ответ: нет правильного.
8. Некоторая страховая компания выплачивает страховую сумму в среднем по 4% договоров. Сколько нужно застраховать клиентов, чтобы с вероятностью 0,94 можно было утверждать, что доля получивших страховую сумму среди них отклонится по абсолютной величине от вероятности получения каждым клиентом страховой суммы не более, чем на 0,01?
А. 1358
Б. 37
В. 8
Г. 94
Решение:
p =0,04 P =0,94 e=0,01
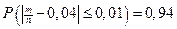
Воспользовавшись формулой
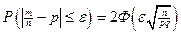 , получим:
, получим:

Значению функции Ф(t), равному 0,47, соответствует значение аргумента, равное t=1,88. Тогда:
 , Þ n»1358,8=1359
, Þ n»1358,8=1359
Ответ: А.
9. Охотник стреляет три раза по удаляющейся цели. Вероятность попадания в цель в начале стрельбы равна 0,9, а после каждого выстрела уменьшается на 0,1. Найти математическое ожидание и дисперсию количества попаданий по цели.
А 
Б. 
В. 
Г. 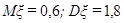
Решение:
Вероятности попадания при первом, втором и третьем выстреле равны соответственно 0,9, 0,8, 0,7, а промаха – 0,1, 0,2, 0,3.
Определим возможные значения случайной величины Х и их вероятности:
Х=0: 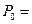 0,1×0,2×0,3=0,006
0,1×0,2×0,3=0,006
Х=1: 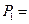 0,9×0,2×0,3+0,1×0,8×0,3+0,1×0,2×0,7=0,092
0,9×0,2×0,3+0,1×0,8×0,3+0,1×0,2×0,7=0,092
Х=2: 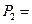 0,9×0,8×0,3+0,9×0,2×0,7+0,1×0,8×0,7=0,398
0,9×0,8×0,3+0,9×0,2×0,7+0,1×0,8×0,7=0,398
Х=3:  0,9×0,8×0,7=0,504
0,9×0,8×0,7=0,504
Запишем ряд распределения
| x | ||||
| p | 0,006 | 0,092 | 0,398 | 0,504 |
Математическое ожидание и дисперсия находятся по формуле:


D(X)=6,22-2,42=0,46
Ответ: А.
10. Студент знает 24 вопросов из имеющихся 30 вопросов программы некоторой учебной дисциплины. На экзамене ему предлагается три наугад выбранных вопроса из программы. Рассматривается случайная величина ξ – число известных вопросов студенту. Найти 
А. 0,4985
Б. 0,0887
В. 0,4079
Г. 0,0049
Решение:
Определим возможные значения случайной величины Х и их вероятности:
Х=0: 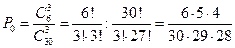 =0,0049
=0,0049
Х=1:  =0,0887
=0,0887
Х=2:  =0,4079
=0,4079
Х=3: 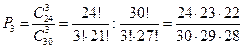 =0,4985
=0,4985
Запишем ряд распределения
| x | ||||
| p | 0,0049 | 0,0887 | 0,4079 | 0,4985 |
Найдем математическое ожидание:

Тогда Р(X³MX)=Р(X³2,4)=0,4985
Ответ: А.
Список литературы
- Бородин, Андрей Николаевич. Элементарный курс теории вероятностей и математической статистики: учеб. пособие для вузов по немат. специальностям / А. Н. Бородин.- 7-е изд., стер.- СПб. [и др.]: Лань, 2008.
2. Гмурман, Владимир Ефимович. Теория вероятностей и математическая статистика: учеб. пособие для вузов / В. Е. Гмурман.- 9-е изд.,стер.- М.: Высш. шк., 2003.
- Семенов, Александр Трофимович. Теория вероятностей: Учебное пособие / А.Т.Семенов;НГАЭиУ.- Новосибирск, 2002.
- Теория вероятностей и математическая статистика: учеб. пособие для вузов по направлению "Экономика" и др. экон. специальностям / [Л. Г. Бирюкова и др.]; под ред. В. И. Ермакова; Рос. экон. акад. им. Г. В. Плеханова.- М.: ИНФРА-М, 2010.






