Координаты середины векторов вычисляются по формуле:
- где C - координата середины, К - конца, Н - начала:
Пусть середина MN - С, тогда:
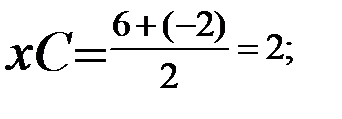
А (-2;8); С (2;-2)
Данные точки лежат на одной прямой. Через систему уравнений найдём коэффициенты k и b данной прямой y=kx+b, подставив в неё координаты точек:
8 = -2k+b 8 = -2k-2-2k 4k =-10 k = -2,5
-2 = 2k+b b = -2-2k b =-2-2k b = 3
Для полученной прямой y = -2,5x+3 приведём уравнение:
y = -2,5x+3
2,5х+у-3=0
Ответ: 2,5х+у-3=0
2. Найти пределы:
а) 
б) 
а) 
= 
= 
=
= 
= 
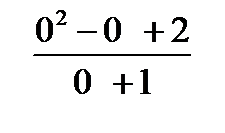= 2
б) =
Разделим числитель и знаменатель на х3
= 
=
Сделаем замену: u=1/x
= 
= 
= - 
3. Найти интегралы:
а) 
; б) 
; в)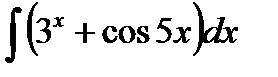 
.
а) = 
- 
+ 
= 
- 
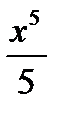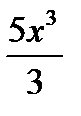+ 3x + C
б) = 8 
= 8 ln x + C
в) =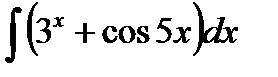 
+ 
= 
+
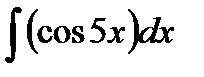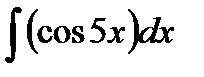
Пусть u=5x.
Тогда пусть du=5dx и подставим dx=du/5:
+ = + 
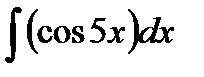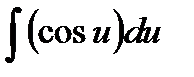= + sin(u)+C= + sin(5x)+C
4. Исследовать функцию и построить график: у = 3х3 – х
Точки пересечения с осью координат Y
График пересекает ось Y, когда x равняется 0:
подставляем x = 0 в 3х3 – х.
3⋅ 03− 0=0
f(0)=0
Точка: (0, 0)
Точки пересечения с осью координат X
График пересекает ось X, когда y равняется 0:
подставляем y = 0 в y=3x3 - x.
3 x3−x =0
x(3 x2−1) =0
x1=0; (3 x2−1) =0
x2= 
x3=-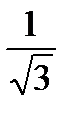 
Точки: (0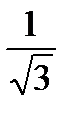, 0); (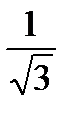,0); (- ,0).
Экстремумы функции
Экстремумы функции
Для того, чтобы найти экстремумы, нужно решить уравнение
f ′(x)=0 (производная равна нулю),
и корни этого уравнения будут экстремумами данной функции:
f ′(x)=(3 x3−x)′ = 9x2 – 1
9x2 – 1 = 0
Решаем это уравнение, получаем:
x1=−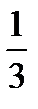 
;
x2= 
.
Значит экстремумы в точках: (− ; 
); (; - 
)
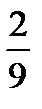Интервалы возрастания и убывания функции.
Найдём интервалы, где функция возрастает и убывает, а также минимумы и максимумы функции, для этого смотрим как ведёт себя функция в экстремумах при малейшем отклонении от экстремума:
Минимум функции в точке x1= ;
Максимум функции в точке x2=− .
Убывает на промежутках (- ∞; − ] U [∞; )
Возрастает на промежутке [ − ; ]
Точки перегибов
Найдем точки перегибов, для этого надо решить уравнение
f ′′(x)=0 (вторая производная равняется нулю),
корни полученного уравнения будут точками перегибов для указанного графика функции,
f ′′(x)= (3 x3−x)′′= (9x2 – 1)′ = 18x
18x=0
Решаем это уравнение, получаем:
x=0
Интервалы выпуклости и вогнутости.
Найдём интервалы, где функция выпуклая или вогнутая, для этого посмотрим, как ведет себя функция в точках перегибов:
Вогнутая на промежутках
[ 0, ∞)
Выпуклая на промежутках
(-∞, 0 ]
Горизонтальные асимптоты
Горизонтальные асимптоты найдём с помощью пределов данной функции при x→∞ и x→ - ∞
(3x3-x)= - ∞ значит,
горизонтальной асимптоты слева не существует.
(3x3-x)= ∞ значит,
горизонтальной асимптоты справа не существует.
Наклонные асимптоты
Наклонную асимптоту можно найти, подсчитав предел функции 3x3-x, делённой на x при x→∞ и x→ - ∞
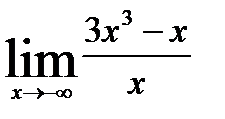= ∞ значит,
наклонной асимптоты слева не существует.
= ∞ значит,
наклонной асимптоты справа не существует.
Чётность и нечётность функции
Проверим чётность и нечётность функции с помощью соотношений
f = f(-x) и f = -f(-x).
Итак, проверяем:
3x3-x = -3 x3+x Нет
3x3-x = -(-3 x3+x) Нет
значит, функция не является ни чётной, ни нечётной.
5.Решить дифференциальное уравнение:
у(0)=5
Представим исходное дифференциальное уравнение в виде:
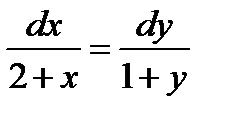или 
Интегрируя обе части, получаем:
ln(y+1) = ln(x+2) + ln(C)
отсюда
y = C (x+2) – 1
Подставляем у(0)=5
5 = C (0+2) – 1
С=(5+1)/2
С=3
Тогда решением дифференциального уравнения будет
y = 3 (x+2) –1
y = 3x+6 – 1
y = 3x+5
