азложение многочлена на множители с помощью формул сокращенного умножения.

ормулы сокращённого умножения.

1. а²-b²=(a-b)(a+b) - разность квадратов

2. (a+b)²=a²+2ab+b² – квадрат суммы

3. (a-b)²=a²-2ab+b² – квадрат разности

4. a³+b³=(a+b)(a²-ab+b²) – сумма кубов

5. a³-b³=(a-b)(a²+ab+b²) – разность кубов

6. (a+b)³=a³+3a²b+3ab²+b³ – куб суммы

7. (a-b)³=a³-3a²b+3ab²-b³ – куб разности

Пример 1. Раскрыть скобки в выражении: (3х + 2)²

Решение. а) Воспользуемся формулой (2), учитывая, что в роли а – выступает 3х, а в роли b — число 2. Получим: (Зх + 2)² = (3х)² + 2∙3х∙2 + 2² = 9x² + 12x + 4.

Пример 2. Вычислить: 79 ∙81 = (80 - 1) (80 + 1)= 80² - 1² = 6400 - 1 = 6399

Пример 3. Вычислить: 71² = (70 + 1)² = 70² + 2∙70∙1 + 1² = 4900 + 140 + 1 = 5041.

Задания по вариантам:

№ варианта	1. Раскройте скобки	2. Вычислите:	3. Решите уравнение:
	a) (а + 3)2; b) (2a +p)2; c) (a-4)2+a(a+8).	a) 792; b) 69∙71.	a) 8х(1+2х)-(4х+3)(4х-3)=2х
	a) (b- 4)2; b) (3c – 2t)2; c) (y-5)2-(y-2).	a) 392; b) 31∙29.	a) х-3х(1-12х)=11-(5-6х)(6х+5)
	a) (с + 3)2; b) (6x – 3k)2; c) (x-7)x+(x+3)2.	a) 592; b) 89∙91.	a)(6х-1)(6х+1)-4х(9х+2)=-1
	a) (m-2)2; b) (7y + 6e)2; c) b(b+4)-(b+2)2.	a) 692; b) 99∙101.	a) (8-9х)х=-40+(6-3х)(6+3х)
	a) (x +1)2; b) (8x + 3y)2; c) (3а-b)(3а+b)+b2.	a) 212; b) 58∙62.	a) (х-6)2-х(х+8)=2
	a) (y-2)2; b) (6m-4n)2; c) 9x2-(y+4x)(y-4x).	a) 312; b) 82∙78.	a) 9х(х+6)-(3х+1)2=1
	a) (a-5)2; b) (9p-2q)2; c) (7m-10n)(7m+10n)-100n2.	a) 612; b) 42∙38.	a) х(х-1)-(х-5)2=2
	a) (c+8)2; b) (10z+3t)2; c) (5c-6d)(5c+6d)-25c2.	a) 422; b) 18∙22.	a) 16х(2-х)+(4х-5)2=1
	a) (7-a)2; b) (3a+5x)2; c) 2(a-2)(a+2).	a) 622; b) 28∙32.	a) 9х2-1-(3х-2)2=0
	a) (9+b)2; b) (6y-5z)2; c) 5c(c+3)(c-3).	a) 282; b) 49∙51.	a) х+(5х+2)2=25(1+х2)

§1.2.Способы разложения многочленов на множители

ынесение общего множителя за скобки.

Алгоритм отыскания общего множителя нескольких одночленов

1. Найти наибольший общий делитель коэффициентов всех одночленов, входящих в многочлен, — он и будет общим числовым множителем (разумеется, это относится только к случаю целочисленных коэффициентов).

2. Найти переменные, которые входят в каждый член многочлена, и выбрать для каждой из них наименьший (из имеющихся) показатель степени.

3. Произведение коэффициента, найденного на первом шаге, и степеней, найденных на втором шаге, является общим множителем, который целесообразно вынести за скобки.

Замечание. В ряде случаев полезно выносить за скобку в качестве общего множителя и дробный коэффициент.

Пример 1. Разложить на множители: -х⁴у³-2х³у² + 5х².

Решение. Воспользуемся сформулированным алгоритмом.

1) Наибольший общий делитель коэффициентов -1, -2 и 5 равен 1.

2) Переменная х входит во все члены многочлена с показателями соответственно 4, 3, 2; следовательно, можно вынести за скобки х².

3) Переменная у входит не во все члены многочлена; значит, ее нельзя вынести за скобки.

В ы в о д: за скобки можно вынести х². Правда, в данном случае целесообразнее вынести за скобки -х².

Получим: -х⁴у³-2х³у² + 5х² = -х²(х²у³+2ху²-5)

Задания по вариантам:

№ варианта	1. Разложить на множители	2. Вычислите наиболее рациональным способом
	a) 3х+3у b) 2,4x+7,2y c) 2z5q2-4z3+6z2q3	a) 1542+154∙46
	a) 3x+6y b) 1,8x-2,4y c) xy3+5x2y2-3x2y	a) 0,23+0,22∙0,8
	a) 5a-5b b) 0,01a+0,03b c) 7a4b3-14a3b4+21a2b5	a) 1672-167∙67
	a) 5a-15b b) 1,25x-1,75a c) 8x3y3+88x2y3-16x3y4	a) 0,92-0,81∙2,9
	a) 7a+7y b) 0,5a-1,5c c) 15x3y2+10x2y-20x2y3	a) 1322-132∙32
	a) 7a+14y b) 0,01a+0,05b c) 12a2b4-36a2b+44abc	a) 252+25∙75
	a) 8x-8a b) 0,001a+0,005b c) 195c6p5-91c5p6+221c3p10	a) 1832-183∙83
	a) 8x-32a b) 0,18x+0,24y c) 42a4b-48a3b2-78a2b3	a) 0,43+0,32∙0,6
	a) 15a-25b b) 0,24x-0,72y c) 35x3y2+15x2y2-20x2y3	a) 312+31∙69
	a) 12d-6v b) 0,03a+0,09b c) 8x3y3-88x2y3+32x3y4	a) 312+31∙169

пособ группировки.

Алгоритм способа группировки

1. Выполнить группировку слагаемых, имеющих общий множитель;

2. Отдельно в каждой группе найти общий множитель и вынести его за скобки;

3. В получившемся выражении найти общий множитель и вынести его за скобки.

Пример 1. Разложить на множители многочлен 2а² + 6а + аb + 3b.

Решение.

1. Объединим в одну группу первые два члена, а в другую — последние два члена многочлена: (2а² + 6а) + (аb + 3b).

2. Замечаем, что в первой группе можно вынести за скобки 2а, a

во второй группе b. Имеем: 2а (а + 3) + b (а + 3).

3. Теперь мы видим, что «проявился» общий множитель (а + 3), который можно вынести за скобки. В результате получим: (а + 3) (2а + b).

Задания по вариантам:

№ варианта	1. Разложите на множители:	2. Вычислите наиболее рациональным способом:
	a) 3а+3-na-n b) 16аb2+ 5b2с + 10с3+ 32ас2	a) 2,7∙6,2 - 9,3∙1,2 + 6,2∙9,3 - 1,2∙2,7
	a) 6mx-2m+9x-3 b) 18а2 + 27аb + 14ас + 21bс	a) 125∙48 - 31∙82 - 31∙43 - 125∙83
	a) ax-3x-4a+12 b) 20n2 - 35а - 14аn + 50n	a) 14,9∙1,25+0,75∙1,1+14,9∙0,75+1,1∙1,25
	a) 2mx-3m-4x+6 b) 2x2yz – 15yz – 3xz2+ 10ху2.	a) 109∙9,17-5,37∙72-37∙9,17+ 1,2∙72
	a) 7kn-6k+14n-12 b) 40a3bc+21bc - 56ac2 - 15a2b2	a) 19,9∙18-19,9∙16+30,1∙18-30,1∙16
	a) 5a2-5ax-7a+7x b) 16xy2 - 5y2z - 10z3+ 32xz2	a) 15,5∙20,8+15,5∙9,2-3,5∙20,8-3,5∙9,2
	a) 9m2-9mn-5m+5n b) 30x2+10c - 25cx - 12x	a) 77,3∙13+8∙37,3 - 77,3∙8 - 13∙ 37,3.
	a) 6a2-2ab-3ac+bc b) 18x2z -10kxy+20k2y-36kxz.	a) 19,9∙19-19,9∙17+30,1∙19-30,1∙17
	a) 7c2-c-c3+7 b) ax2 - ay - bx2 + cy + by- cx2	a) 15,5∙20,7+15,5∙9,3-3,5∙20,7-3,5∙9,3
	a) x3-6+2x-3x2 b) xy2 - by2 - ax + ab + y2- a	a) 77,3∙15+9∙37,3 - 77,3∙9 - 15∙ 37,3.

азложение многочлена на множители с помощью формул сокращенного умножения.

Любой из формул сокращённого умножения можно пользоваться как для сокращенного умножения многочлена на многочлен, так и для разложения многочлена на множители.

Пример1. Разложить на множители 64х²-9

Решение: В примере воспользуемся формулой (1) (разность квадратов)

64х²-9=(8х)²-3²=(8х-3)(8х+3).

Пример2. Разложить на множители а²-4аb+4b²

Решение: В примере даны трехчлены, для их разложения на множители будем пользоваться формулами (2 и 3), если, конечно, убедимся в том, что трехчлен является полным квадратом:

а² - 4аb + 4b² = а² - 2∙2a+(2b)² =(a-2b)²

Мы убедились, что трехчлен содержит сумму квадратов одночленов а и 2b, а также удвоенное произведение этих одночленов.

Пример 3. Разложить на множители 125а³-8b³

Решение. Здесь воспользуемся формулами (4 и 5) (разность и сумма кубов).

125а³ - 8b³ =(5а)³ –(2b)³=(5a-2b)(25a²-10ab+4b²)

Задания по вариантам

№ варианта	1. Разложите на множители:	2. Вычислите наиболее рациональным способом:
	a)x2y2-1 b)a3+8 c) a2-2ab+b2	а) 342+ 2∙ 34∙ 36 + 362
	a)c2d2 b)b3-27 c) x2+2xy+y2	a) 272 - 2 ∙ 27 ∙ 13 + 132
	a)m2n2-25 b)с3-64 c) z2+2zt+t2	a) 982 - 2 ∙ 98 ∙ 8 + 82
	a)p2q2-100 b)d3+125 c) m2-2mn+n2	a) 76,42 + 13,62 + 2 ∙76,4 ∙ 13,6
	a)25-36p2c2 b)216-m3 c) m2+4m+4	а) 2572 - 1432
	a)100m2n2-81 b)1000+m3 c)a2-12a+36	a) 73,62 - 26,42
	a)49x2y2-400 b)729+p3 c)1-2b+b2	a) 1652 - 652
	a)225-144c2d2 b)343-q3 c)y2+18y+81	a) 72,52-47,52
	a)c2d2-m2 b)64a3+1 c)p2+10p+25	a)1272-272
10	a)a2x2+0.25y2 b)27d3-8 c)x2-14x+49	a)1382-382

§1.3.Решение линейных уравнений и неравенств

§1.3.1 Линейные уравнения

Определение: Уравнение вида ах=b, где х – переменная, а и b – числа, называется линейным уравнение с одной переменной.

Число а называется коэффициентом при переменной, а число b – свободным членом.

Уравнения обладают следующими свойствами:

1. Если к обеим частям уранения прибавить одно и то же число, то получится уравнение, равносильное данному;

2. Если обе части уравнения умножить или разделить на одно и то же отличное от нуля число, то получится уравнение, равносильное данному.

Пример1: Решить уравнение 4(х+7)=3-х

Расскроем скобки: 4х+28=3-х

Перенесем слагаемое – х в левую часть уравнения, а слагаемое 28 в правую, изменив при этом их знаки: 4х+х=3-28.

Приведем подобные слагаемые: 5х=-25.

Разделим обе части уравнения на 5: х=-5

Ответ: х=-5.

Задача 1. В корзине было в 2 раза меньше яблок, чем в ящике. После того как из корзины переложили в ящик 10 яблок, в ящике их стало в 5 раз больше, чем в корзине. Сколько яблок было в корзине и сколько в ящике?

Решение. Пусть в корзине было х яблок, тогда в ящике было 2х яблок. После того как из корзины переложили в ящик 10 яблок, в корзине стало (х —10) яблок, а в ящике (2х+10) яблок. По условию задачи в ящике стало в 5 раз больше яблок, чем в корзине. Значит,

5 (х —10) = 2х+10.

Решим составленное уравнение:

5х —50 = 2х + 10,

5х-2х=10 + 50,

3х = 60,

х = 20.

Следовательно, в корзине было 20 яблок. Так как 2х = 2∙20 = 40, то в ящике было 40 яблок.

Задания по вариантам

№ варианта	1. Решить уравнение	2. Решить задачу
	a) 4x-1,6=0 b) (y+4) - (у -1)=6у	a) Периметр треугольника равен 16 см. Две его стороны равны между собой и каждая из них на 2,9 см больше третьей. Каковы стороны треугольника?
	a) 38+2x=0 b) 3р- 1-(р + 3)=1.	a) В трех цехах завода работают 1274 человека. Во втором цехе на 70 человек больше, чем в первом, а в третьем на 84 человека больше, чем во втором. Сколько человек работают в каждом цехе?
	a) 30-6x=0 b) 6 (v + 2) - 7v = 101	a) На свитер, шапку и шарф израсходовали 555 г шерсти, причем на шапок ушло на 320 г шерсти меньше, чем на свитер, и на 5 г больше, чем на шарф. Сколько шерсти израсходовали на каждое изделие?
	a) 35-7,5x=0 b) 20u=19 –(3 + 12u).	a) Можно ли расположить 158 книг на трех полках так, чтобы на первой полке было на 8 книг меньше, чем на второй, и на 5 книг больше, чем на третьей?
	a) 0,9-81x=0 b) 2х + 5 = 2 (х + 1) + 11	a) Можно ли 59 банок консервов разложить в три ящика так, чтобы в третьем было на 9 банок больше, чем в первом, а во втором на 4 банки меньше, чем в третьем?
	a) 144+12x=0 b) 5 (2у - 4) = 2 (5у - 10);	a) На одном садовом участке в 5 раз больше кустов малины, чем на другом. После того как с первого участка пересадили на второй 22 куста, на обоих участках кустов малины стало поровну. Сколько кустов малины было на каждом участке?
	a) 15x-3=0 b) 3у - (у - 19) = 2у	a) В одном резервуаре 380 м3 воды, а в другом 1500 м3. В первый резервуар каждый час поступает 80 м3 воды, а из второго каждый час выкачивают 60 м3. Через сколько часов воды в резервуарах станет поровну?
	a) 150x-0,3=0 b) 6х = 1-(4 -6х).	a) Перчатки на 6 р. дешевле портфеля и на 2 р. дороже берета. Сколько стоят перчатки, если 2 портфеля стоят столько же, сколько стоят 7 беретов?
	a) 12x-6=0 b) 3у + (у - 2)= 2 (2у - 1);	a) По шоссе идут две автомашины с одной и той же скоростью. Если первая увеличит скорость на 10 км/ч, а вторая уменьшит на 10 км/ч, то первая за 2 ч пройдет столько же, сколько пройдет вторая за 3 ч. С какой скоростью идут автомашины?
	a) 0,24x-4=0 b) 6у - (у - 1)=4 + 5y	a) В первой бригаде было в 4 раза меньше людей, чем во второй. После того как из второй бригады 6 человек ушло, а 12 перевели в первую, людей в бригадах стало поровну. Сколько человек было в первой бригаде?

§1.3.2 Линейные неравенства

Свойства числовых неравенств позволяют руководствоваться при решении неравенств следующими правилами:

Правило 1. Любой член неравенства можно перенести из одной части

неравенства в другую с противоположным знаком, не изменив при этом знак неравенства.

Правило 2. Обе части неравенства можно умножить или разделить на одно

и то же положительное число, не изменив при этом знак неравенства.

Правило 3. Обе части неравенства можно умножить или разделить на одно

и то же отрицательное число, изменив при этом знак неравенства на противоположный.

Пример 1. Решить неравенство Зх - 5 > 7х - 15.

Решение. Перенесем член 7х в левую часть неравенства, а член - 5 — в правую часть неравенства, не забыв при этом изменить знаки и у члена 7х, и у члена - 5 (руководствуемся правилом 1). Тогда получим Зх - 7х > - 15 + 5, т. е. - 4х > - 10.

Разделим обе части последнего неравенства на одно и то же отрицательное число - 4, не забыв при этом перейти к неравенству противоположного смысла (руководствуясь правилом 3).

Получим х < 2,5. Это и есть решение заданного неравенства.

О т в е т: х < 2,5, или (- ; 2,5].

Пример 2. Решить неравенство

Решение. Умножим обе части неравенства на положительное число 15, оставив знак неравенства без изменения (правило 2). Это позволит нам освободиться от знаменателей, т. е. перейти к более простому неравенству, равносильному данному:

5х + 3(2х-1)>30х-1;

5х + 6х - 3 > 30х - 1;

11х-3>30х-1.

Воспользовавшись для последнего неравенства правилом 1, получим равносильное ему более простое неравенство:

11х - 30х > - 1 + 3, т. е.

-17х>2.

Наконец, применив правило 3, получим

Ответ:

Задания по вариантам

№ варианта	1. Решить неравенство:
	a) 2а-11 >а + 13; b) 10х + 9 > - 3(2 - 5х); c)
	a) 8b + 3 < 9b - 2; b) 2(3 – 2z)+ 3(2-z) < 40; c)
	a) 6-4с>7-6с; b) 2(х + 1) – 1< 7 +8x c)
	a) 3-2х< 12 -5х. b) – 2(4z + 1) < 3 – 10z; c)
	a) d-5>3-d; b) 8 + 6р < 2(5р - 8); c)
	a) 3m + 17<m-13; b) 3(2-4n)>6-3n c)
	a) р + 4>12 + 9р. b) –(6y+2)>6(y-1) c)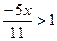
	a) -2x + 12>3x-3; b) 7-16r>-2(8r-1)+5 c)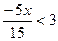
	a) 3t+5>7t-7 b) 4(а + 1) + За > 7а + 2; c)
	a) 6y+8>10y-8 b) 2(6y+2)<3(y-1) c)

§1.4.Построение графиков квадратичной функции

 

Определение: Квадратичной функцией называется функция, которую можно задать формулой вида y=ax²+bx+c, где х - независимая переменная, a, b и с -некоторые числа (причём а≠0).

Определение: Графиком квадратичной функции является парабола, ветви которой направлены вверх (если а>0) или вниз (если а<0).

§1.4.1 Построение графика функции y=ax²+bx+c

1. Описать функцию: название функции, что является графиком функции, куда направлены ветви параболы.

2. Найти координаты вершины параболы А(m;n) по формулам: , ; или n = у(m) т.е. подставить найденное значение абсциссы m в формулу, которой задана функция и вычислить значение. Прямая x=m является осью симметрии параболы"

3. Заполнить таблицу значений функции, в ней расположить вершину в середине таблицы и взять соседние симметричные значения х (посчитать значение функции в выбранных значениях х)

4. Построить график функции: отметить в координатной плоскости точки, координаты которых указаны в таблице; соединить их плавной линией.

Пример 1: Построить график функции y=x²+2x+1

1. Квадратичная функция, графиком является парабола, ветви которой направленны вверх;

2. Нахождение вершины А(m;n)

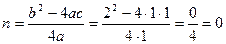
A(-1;0)

3. Таблица значений

х	-4	-3	-2	-1
у

4. График

§1.4.2 Параллельный перенос вдоль оси ординат на вектор (0;b)

Для построения графика функции 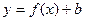(где b – постоянное число), надо перенести график функции на вектор (0;b) вдоль оси ординат.

Пример 2: Поcтроить график функции у=х²-3

y=х2-3

y=х2

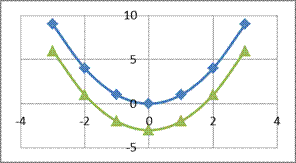
§1.4.3 Параллельный перенос вдоль оси абсцисс на вектор (а;0)

График функции получается из графика функции переносом вдоль оси абсцисс на вектор (а;0). При а>0 вектор (а;0) направлен в положительном направлении оси абсцисс, при а<0 – в отрицательном.

Пример 3: Поcтроить график функции у=(х-3)²