еобходимое и достаточное условие экстремума.
Если для функции z = f(x, y), определенной в некоторой области, в некоторой окрестности точки М0(х0, у0) верно неравенство
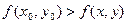
то точка М0 называется точкой максимума.
Если для функции z = f(x, y), определенной в некоторой области, в некоторой окрестности точки М0(х0, у0) верно неравенство
то точка М0 называется точкой минимума.
еорема. (Необходимые условия экстремума).
Если функция f(x,y) в точке (х0, у0) имеет экстремум, то в этой точке либо обе ее частные производные первого порядка равны нулю 
, либо хотя бы одна из них не существует.
Эту точку (х0, у0) будем называть критической точкой.
еорема. (Достаточные условия экстремума).
Пусть в окрестности критической точки (х0, у0) функция f(x, y) имеет непрерывные частные производные до второго порядка включительно. Рассмотрим выражение:
1) Если D(x0, y0) > 0, то в точке (х0, у0) функция f(x, y) имеет экстремум, если
- максимум, если 
- минимум.
2) Если D(x0, y0) < 0, то в точке (х0, у0) функция f(x, y) не имеет экстремума
В случае, если D = 0, вывод о наличии экстремума сделать нельзя.
Пример. Исследовать функцию 
на экстремум.
Находим частные производные первого порядка и приравниваем их к нулю:
Стационарная точка данной функции имеет координаты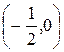 
.
Вычислим вторые производные 
.
Следовательно, 
.
Экстремум имеется, т.к. 
, то в точке 
- минимум,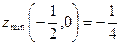 
.
Метод множителей Лагранжа основан на том, что точка условного экстремума 
функции 
при условии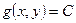 
соответствует точке экстремума 
функции 
. Функция L называется функцией Лагранжа, а 
- множителем Лагранжа.
Для выполнения этого условия во всех точках найдем неопределенный коэффициент l так, чтобы выполнялась система трех уравнений:
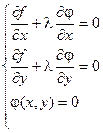
Полученная система уравнений является необходимыми условиями условного экстремума. Однако это условие не является достаточным. Поэтому при нахождении критических точек требуется их дополнительное исследование на экстремум.
Пример. Найти экстремум функции f(x, y) = xy, если уравнение связи:
2x + 3y – 5 = 0
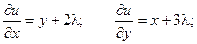
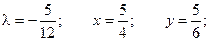
Таким образом, функция имеет экстремум в точке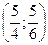 
.
етод градиентного спуска.
В случае функций нескольких переменных одним из наиболее простых численных методов отыскания экстремума является метод градиентного спуска. Из курса математического анализа известно, что градиент функции 
равен 
и направлен в сторону наискорейшего возрастания функции. Следовательно, при поиске минимума рационально двигаться в направлении, противоположном градиенту.
Пусть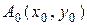 
начальное приближение минимума, последующее приближение 
находим по формуле
, (1)
где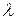 
находится из условия минимизации зависящей от 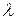функции
.
Данную формулу используют итерационно до тех пор, пока не будет достигнута требуемая точность. При этом могут быть использованы критерии останова итераций, рассмотренные в методе координатного спуска.
ример.
Найти минимум функции 
методом градиентного спуска, приняв за начальное приближение точку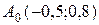 
.
Находим градиент функции 
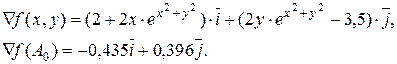
Определяем минимум функции
пользуясь численным методом поиска экстремума функций одного переменного. В результате имеем 
. По формуле (1) вычисляем приближение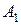 
.
Точка 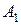является приближенным решением задачи, более точным чем заданное начальное приближение 
. Если точку 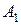взять за начальное приближение, то аналогично получим точку 
еще ближе отстоящую от точки минимума и так далее.
