аздел 2. ЭЛЕМЕНТЫ ТЕОРИИ ГРАФОВ.
Основные определения теории графов
Граф – математический объект, описываемый двумя множествами: G= (V, E), где V – так называемое множество вершин, а E – множество дуг.
Элементами множества дуг являются упорядоченные пары вершин, т.е. E ={ (a, b): a Î V, b Î V }, т.о. множество Е является подмножеством декартова произведения V ´ V. Порядок вершин в парах может и не учитываться, тогда элементы множества Е называют ребрами, а сам граф – неориентированным графом, в противном случае – ориентированным или Орграфом. В некоторых случаях рассматриваются так называемые смешанные графы, в них множество Е состоит из элементов обоих видов: дуг и ребер.
Обозначим вершины v 1, v 2, v 3, ¼, а ребра e 1, e 2, e 3, ¼. Вершины vi и vj, определяющие ребро ek, называются концевыми вершинами ребра ek =(vi, vj), а в случае орграфа – началом и концом дуги ek соответственно. Говорят также, что ребро ek (дуга) инцидентно вершинам vi, vj или, что вершины vi, vj инцидентны ребру (дуге) ek. Такие вершины называют смежными. Ребра называют смежными в случае, когда они имеют общую концевую вершину. Например, ek =(vi, vj) и em =(vi, vl) – смежные ребра.
В множестве ребер графа допускается более, чем одно ребро с одинаковыми концевыми вершинами. Такие ребра называются параллельными или кратными. Например: ek =(vi, vj) и em =(vi, vj) – кратные ребра.
Если обе концевые вершины ребра совпадают, то такое ребро называется петлей. Например: ek =(vi, vi) – петля.
Граф без петель и параллельных ребер называется простым, в противном случае – мультиграфом.
Граф, не имеющий ребер, называется пустым, а не имеющий вершин (а значит и ребер) – нуль‑графом.
Простой граф, у которого любая пара вершин смежна, называется полным.
Количество вершин в графе называется порядком графа.
Степенью или валентностью вершины называется число инцидентных ей ребер. Будем обозначать степень вершины vi – deg(vi). Вершина нулевой степени называется изолированной. Вершина степени 1 называется висячей, а ребро, инцидентное ей, называется висячим ребром. Заметим, что петля добавляет двойку к степени вершины.
пособы задания графов.
Рассмотрим три способа задания графов: графический, аналитический и матричный.
1) Графический способ.
Вершины изображают точками на плоскости, а ребра – линиями, соединяющими соответствующие точки. Для изображения дуги используется линия со стрелкой, указывающей направление от начала к концу дуги.
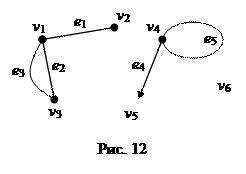 На рисунке 12 изображен смешанный граф с вершинами v 1, v 2,¼, v 6, ребрами e 1, e 2, e 3, e 5 и дугой e 4. Смежные вершины v 1, v 2, инциденты ребру e 1. Вершины v 1, v 3, инциденты параллельным ребрам e 2 и e 3. Вершине v 4 инциденты петля e 5 и дуга e 4, причем v 4 является началом дуги e 4, а v 5 – концом этой дуги. Степень вершины v 1 равна 3, вершины v 2 – 1, вершины v 3 – 2, вершины v 4 – 3, вершины v 5 – 1, вершины v 6 – 0. Таким образом, вершины v 2 и v 5 – висячие, а вершина v 6 – изолированная. В случае дуги e 4 точнее было бы говорить о полустепенях исхода и захода вершин v 4 и v 5, а именно: полустепень исхода вершины v 4 равна 3, вершины v 5 – 0, полустепень захода вершины v 4 равна 2, вершины v 5 – 1.
На рисунке 12 изображен смешанный граф с вершинами v 1, v 2,¼, v 6, ребрами e 1, e 2, e 3, e 5 и дугой e 4. Смежные вершины v 1, v 2, инциденты ребру e 1. Вершины v 1, v 3, инциденты параллельным ребрам e 2 и e 3. Вершине v 4 инциденты петля e 5 и дуга e 4, причем v 4 является началом дуги e 4, а v 5 – концом этой дуги. Степень вершины v 1 равна 3, вершины v 2 – 1, вершины v 3 – 2, вершины v 4 – 3, вершины v 5 – 1, вершины v 6 – 0. Таким образом, вершины v 2 и v 5 – висячие, а вершина v 6 – изолированная. В случае дуги e 4 точнее было бы говорить о полустепенях исхода и захода вершин v 4 и v 5, а именно: полустепень исхода вершины v 4 равна 3, вершины v 5 – 0, полустепень захода вершины v 4 равна 2, вершины v 5 – 1.
2) Аналитический способ.
Граф задают перечислением элементов множества вершин и множества ребер. Для графа, изображенного на рисунке 12, эти множества: V ={ v 1, v 2, v 3, v 4, v 5, v 6} и Е ={ e 1, e 2, e 3, e 4, e 5}, где e 1=(v 1, v 2), e 2=(v 1, v 3), e 3=(v 1, v 3), e 4=(v 4, v 5), и e 5=(v 4, v 4).
3) Матричный способ.
Имеется несколько вариантов задать граф матрицей. Наиболее употребимыми являются матрица инциденций и матрица смежности.
а) Матрица инциденций – это прямоугольная матрица, число строк которой равно числу вершин, а число столбцов – числу дуг (ребер) графа. Элементы этой матрицы определяются следующим образом:
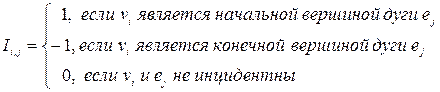
Таким образом, для графа на рисунке 12 матрица инциденций такова:
| e 1 | e 2 | e 3 | e 4 | e 5 | ||
| v 1 | ||||||
| v 2 | ||||||
| I= | v 3 | |||||
| v 4 | ||||||
| v 5 | -1 | |||||
| v 6 |
По этой матрице легко судить о наличии в графе параллельных ребер (два одинаковых столбца), петли (одна единица в столбце), дуги (значения разных знаков в столбце), изолированной вершины (нулевая строка), висячих вершин (одно ненулевое значение в строке).
б) Матрица смежности вершин – это квадратная матрица, размер которой определяется числом вершин в графе. Элементы этой матрицы определяются так: 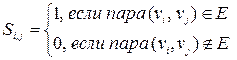 . Если в графе имеются параллельные ребра, то соответствующий элемент матрицы смежности полагают равным числу этих ребер. Так матрица смежности для графа на рисунке 12 такова:
. Если в графе имеются параллельные ребра, то соответствующий элемент матрицы смежности полагают равным числу этих ребер. Так матрица смежности для графа на рисунке 12 такова:
| v 1 | v 2 | v 3 | v 4 | v 5 | v 6 | ||
| v 1 | |||||||
| v 2 | |||||||
| S= | v 3 | ||||||
| v 4 | |||||||
| v 5 | |||||||
| v 6 |
По виду этой матрицы также несложно судить о наличии в графе кратных ребер, дуг, петель, висячих и изолированных вершин.
еоремы о степенях вершин и изоморфизм графов.
Теорема 1: Сумма степеней вершин в неориентированном графе четна и равна удвоенному числу ребер.
Аналогичная теорема может быть сформулирована и для орграфов: сумма полустепеней исхода всех вершин равна сумме их полустепеней захода и равна числу дуг орграфа.
Теорема 2:Число вершин нечетной степени в любом графе четно.
Два графа G 1 и G 2 называются изоморфными, если существует биективное отображение между множествами их вершин и ребер такое, что соответствующие друг другу по этому отображению ребра графов G 1 и G 2 инцидентны соответствующим друг другу по этому же отображению парам вершин этих графов.
Согласно определению, графы, изображенные на рисунке 13, изоморфны. Соответствие между множествами вершин и ребер таково:
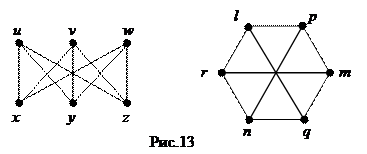 |
для вершин: 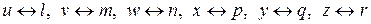
для ребер: 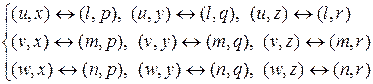
Подграфы
Подграфом графа G =(V, E) называется граф G ¢=(V ¢, E ¢), у которого множества вершин и ребер V ¢ и E ¢ являются такими подмножествами множеств V и E соответственно, что ребро (vi, vj)Î E ¢ тогда и только тогда, когда вершины vi и vj Î V ¢. Граф G ¢ называется собственным подграфом графа G, если V ¢Ì V и E ¢Ì E. Если все вершины графа G присутствуют в его подграфе G ¢, т.е. V ¢= V, то G ¢ называется остовным подграфом G.
Подграф без изолированных вершин называется реберно-порожденным подграфом. Множество вершин реберно-порожденного подграфа полностью определяется множеством его ребер.
Если же множество вершин подграфа полностью определяет множество его ребер, то такой подграф называется вершинно-порожденным. Заметим, что множество ребер вершинно-порожденного подграфа является таким максимальным подмножеством множества ребер графа, что концевые вершины всех этих ребер принадлежат подграфу.
На рисунке 14 изображены: (а) исходный граф; (б) собственный подграф; (в) остовный подграф; (г) реберно-порожденный подграф; (д) вершинно-порожденный подграф.

перации над графами.
1) Объединение двух графов G =(V, E) и G ¢=(V ¢, E ¢) есть граф S =(V ∪ V ¢, E ∪ E ¢).
На рисунке 15 показано объединение двух графов.
 |
 |
2) Пересечение двух графов G =(V, E) и G ¢=(V ¢, E ¢) есть граф S =(V ∩ V ¢, E ∩ E ¢). См. рис.16.
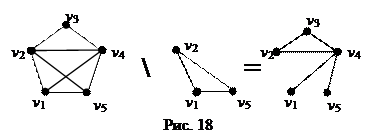
4) Относительное дополнение подграфа до графа – это граф, в который входят те ребра основного графа, которых не было в подграфе, а множество вершин совпадает с множеством вершин основного графа. См. рис.18.
 |
3) Кольцевая сумма двух графов G Å G ¢ есть граф, не имеющий изолированных вершин и состоящий только из ребер, присутствующих либо в G, либо в G ¢, но не в обоих графах одновременно. Т.о. это Е Å Е ¢ реберно-порожденный граф. См. рис.17.
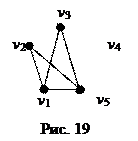 5) Абсолютное дополнение – это дополнение до полного графа на том же множестве вершин. Так для графа, изображенного в правой части равенства на рис.18, абсолютное дополнение будет изображаться так, как показано на рис.19.
5) Абсолютное дополнение – это дополнение до полного графа на том же множестве вершин. Так для графа, изображенного в правой части равенства на рис.18, абсолютное дополнение будет изображаться так, как показано на рис.19.
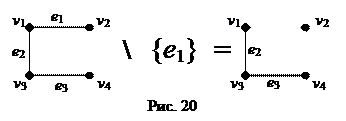 |
6) Удаление ребра – ребро удаляется из графа, а инцидентные ему вершины остаются. См.рис.20.
7) Удаление вершины – вершина удаляется из графа вместе со всеми инцидентными ей ребрами. См. рис.21.
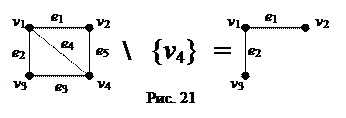 |
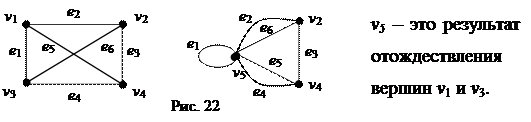 |
8) Отождествление (замыкание) вершин – при замыкании двух вершин, эти вершины удаляются из графа и заменяются одной новой, при этом ребра, инцидентные исходным вершинам, теперь будут инцидентны новой вершине.

9) Стягивание ребра – ребро удаляется, а его концевые вершины отождествляются. На рисунке 23 последовательно стягиваются ребра е 1, е 3, е 2.
Примеры решения задач.
Заданы графы 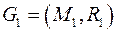 и
и 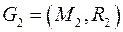 .
. 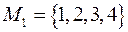 ,
, 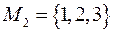 .
.
1. По заданным 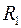 и
и 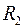 изобразите графы
изобразите графы 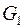 и
и 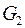 .
.
2. Найдите 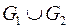 ,
, 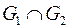 ,
, 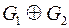 ,
, 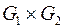 .
.
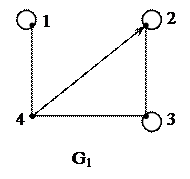
3. Для графа 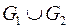 найдите маршруты смежности, инцидентности, сильных компонент, маршрутов длины 2 и все маршруты длины 2, исходящие из вершины 1.
найдите маршруты смежности, инцидентности, сильных компонент, маршрутов длины 2 и все маршруты длины 2, исходящие из вершины 1.
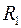 ={(1,1), (1,4), (2,2), (2,3), (3,3), (3,4), (4,1), (4,2), (4,3)}
={(1,1), (1,4), (2,2), (2,3), (3,3), (3,4), (4,1), (4,2), (4,3)}
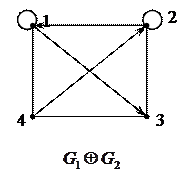
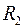 ={(1,3), (2,1), (3,1), (3,3)}
={(1,3), (2,1), (3,1), (3,3)}
 | ||||||||||
 | ||||||||||
 | ||||||||||
| ||||||||||
 |  | |||||||||
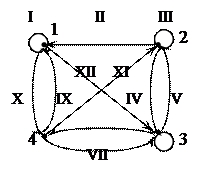
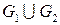 соответствует орграф Матрица смежности
соответствует орграф Матрица смежности
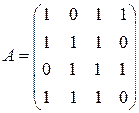 .
.
Матрица инцидентности
I II III IV V VI VII VIII IX X XI XII
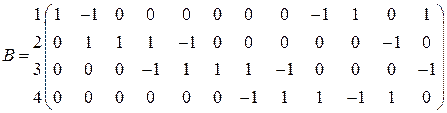 .
.
Матрица достижимости Матрица контрдостижимости
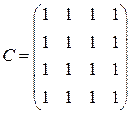
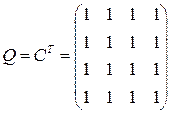 .
.
Матрица сильных компонент 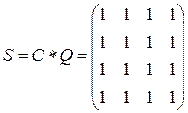 .
.
Матрица маршрутов длины 2:
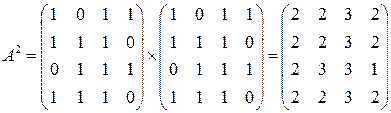 .
.
Все маршруты, длины 2, исходящие из вершины 1 (соответствует 1 строка матрицы А2):
(1,1,1); (1,4,1); (1,3,2); (1,4,2); (1,1,3); (1,3,3); (1,4,3); (1,1,4); (1,3,4).






