Дано:
Код шифратора: 51111
Базис шифратора: ИЛИ
А = 5 – 10000 – множимое число
В = 9 – 11111 – множитель
 1 0 0 0 0
1 1 1 1 1
1 0 0 0 0
1 1 1 1 1
|
| В этом курсовом проекте было построено устройство умножения двоичных положительных чисел. В начале курсового проекта число А – множимое число преобразуется в шифраторе в двоичной системе счисления в код. А число В – множитель подаётся из двоично-десятичного счётчика в коде. Число А и В подаются к устройствам – конъюнктурам или логическим устройствам «ИЛИ» через шину. В нем выполняется операция умножения двоичных чисел. На выходе получаем частичные произведения. Для сдвига хранимого в регистре числа на определённое число разрядов влево используется параллельный регистр Полученные частичные произведения суммируются в сумматоре. После полученный результат подается на параллельный последовательный регистр. В итоге получаем необходимый результат. |
ВВЕДЕНИЕ
В любой сфере человеческой деятельности – в науке, технике, производстве – методы и средства вычислительной техники направлены на повышение производительности труда. Благодаря вычислительной технике почти каждый человек имеет компьютер, мобильный телефон и т.д. Взять ту же вычислительную машинку, в обиходе называемую «калькулятор», ведь это наиболее яркий пример того, где реализовано устройство, которое рассматривается в данной работе.
С помощью этого устройства человек способен посчитать большие числа за доли секунд, просто введя нужные ему цифры и нажав клавишу, за которой закреплена определённая операция. Как уже было сказано выше – существенно повышается производительность труда.
Следует так же обратить внимание на системы счисления. Ведь в зависимости от модели и назначения умножителя – различны и области его применения. Наряду с известной нам десятичной системой счисления существуют:
- двоичная;
- восьмеричная;
- шестнадцатеричная.
К примеру, в двоичной системе используется периодичность нолей и единиц. Эта система счисления наиболее распространена в вычислительной технике, ведь именно в ней информация и передаётся в виде данной последовательности.
Как же было сказано, умножитель двоичных чисел активно применяется в ЭВМ. Производительность ЭВМ в значительной степени определяется временем выполнения операции умножения. Программа реализации операции умножения двух чисел с помощью операции сдвига и сложения требует значительного времени. Наибольшее быстродействие достижимо в умножителях выполненных на основе КС.
В настоящее время применяемые умножители имеют высокое быстродействие и точность. А за счёт развивающихся науки и техники возможен дальнейший рост этих параметров, что в свою очередь приведёт к появлению более мощных, быстрых и дешёвых умножителей; которые будут активно внедряться в ЭВМ, увеличив тем самым её производительность.
Благодаря этому уменьшится количество ЭВМ, которые выполняют данную операцию, т.к. будет хватать меньшего количества компьютеров для выполнения возложенных на него задач. А это приведёт к уменьшению затрат на обслуживание данной техники.
При выполнении данной работы мы будем использовать цифровые устройства как последовательного (автоматы с памятью), так и комбинационные (автоматы без памяти). К автоматам с памятью относятся устройства, которые могут запоминать информацию, поступающие на их вход или входы. К простейшим запоминающим устройствам относятся триггеры, они могут запоминать один бит информации, т.е. цифру 0 или 1. На основе триггеров строятся более сложные устройства, такие как регистры, счётчики. К автоматам без памяти (комбинационным) относятся такие устройства как конъюнктуры, дизъюнкторы, кодирующие устройства, сумматоры и др.
Цифровые устройства по характеру информации на входах и выходах подразделяются на устройства последовательного, параллельного и смешенного действия. В данной курсовой работе нам необходимо будет построить цифровое устройство, выполняющее умножение двух чисел, представленных в двоичной форме.
По способу функционирования цифровые устройства делятся на два класса: комбинационные и последовательные.
1СИНТЕЗ ШИФРАТОРА (У1)
Шифратор преобразует сигнал, поданный только в один входной провод, в выходной параллельный двоичный код на выходах шифратора.
Шифратор - устройство, осуществляющее преобразование десятичных чисел в двоичную систему счисления. Пусть в шифраторе имеется m входов, последовательно пронумерованных десятичными числами (0, 1, 2, 3,..., m - 1) и n выходов. Подача сигнала на один из входов приводит к появлению на выходах n- разрядного двоичного числа, соответствующего номеру возбужденного входа.
Шифраторы широко используются в разнообразных устройствах ввода информации в цифровые системы. Такие устройства могут снабжаться клавиатурой, каждая клавиша которой связана с определенным входом шифратора. Наибольшее применение кодер находит в устройствах ввода информации (пультах управления) для преобразования десятичного числа в двоичную систему счисления. Применение шифраоров приводит к сокращению количества сигналов в цифровых устройствах.
В данной курсовом проекте необходимо построить шифратор, который будет работать в коде Грей в базисе ИЛИ, логические элементы, которые будет содержать наш шифратор – это дизъюнкторы, выполняющие по своему назначению логическое сложение двоичных чисел.
Для начала мы приводим таблицу истинности работы шифратора согласно коду Грей (таблица 1.1). Затем, на основе таблицы истинности записываем функции выходов шифратора, выраженные через дизъюнкцию, после чего строим схему шифратора, выполненную на интегральных логических элементах ИЛИ.
Таблица 1.1 Таблица истинности шифратора
| Десятичные числа | выходы кода 51111 | ||||
| X | У5 | У4 | У3 | У2 | У1 |
Согласно таблице мы записываем функции с учётом того, что входы соответствуют максимальному значению – 1, параметры с 0 – не учитываются.
у1 = х1  х2
х2  х3
х3  х4
х4  х9;
х9;
у2 = х2  х3
х3  х4
х4  х8
х8  х9;
х9;
у3 = х3  х4
х4  х7
х7  х8
х8  х9;
х9;
у4 = х4  y6
y6  х7
х7  х8
х8  х9;
х9;
у5 = х5  y6
y6  х7
х7  х8
х8  х9;
х9;
Х0Х1Х2Х3Х4Х5Х6Х7Х8Х9


Рисунок 1.2 - Микросхема построенного шифратора и его графическое
обозначение
2 ВЫБОР МИКРОСХЕМЫ
ДВОИЧНОДЕСЯТИЧНОГО СЧЁТЧИКА
(У2)
Счётчиком называется последовательное устройство, предназначенное для счета входных импульсов и фиксации их числа. Счет импульсов являеся одной из наиболее распросранненных операций в устройствах дискресной обработки информации.
Счётчики могут строиться на двухступенчатых D-триггерах, T-триггерах и JK-триггерах.
Основной параметр счётчика — модуль счёта — максимальное число единичных сигналов, которое может быть сосчитано счётчиком. Счётчики обозначают через СТ.
В данном курсовом проекте второе число – множитель подаётся из двоично-десятичного счётчика в коде Грей. Счётчик – это цифровой автомат, циклически переходящий из одного состояния в другое под действием сигналов, подаваемых на синхронный вход.
Ксч – число внутренних состояний цифрового автомата.
Если Ксч =2k, где k – целое число, то счётчик называется двоичным.
Если Ксч = 10k-то счётчик является десятичным.
Простейший счётчик – это триггер. Его Ксч =2, так как он может находится в двух состояниях.
По способу переключения триггеров счётчики бывают синхронные и асинхронные. При асинхронном переключении переход триггеров из одного состояния в другое происходит последовательно, а при синхронном - триггеры переключаются одновременно.
Счётчики бывают суммирующие и вычитающие.
Наряду с суммирующими и вычитающими счётчиками находят применение реверсивные счётчики (+, -).
В данном разделе мы будим синтезировать счётчик. Основой для синтеза любого счётчика, как и для любого цифрового устройства, служит так называемая таблица истинности. В данном случае – это таблица кода Грей (таблица 2.1). Для построение счётчика можно использовать Т-триггеры, D-триггеры и JK-триггеры, последний мы и будем использовать для построения. Выбор именно этого триггера обуславливается тем, что с его помощью можно построить и Т-триггер, соединив последовательно вход J и K. Триггер JK - базовый элемент цифровых микросхем, имеющих внутреннюю память. Если выходные сигналы логических элементов и комбинационных микросхем однозначно определяются их текущими входными сигналами, то выходные сигналы микросхем с внутренней памятью зависят также еще и от того, какие входные сигналы и в какой последовательности поступали на них в прошлом, то есть они помнят предысторию поведения схемы. Именно поэтому их применение позволяет строить гораздо более сложные и интеллектуальные цифровые устройства, чем в случае простейших микросхем без памяти.
В JK-триггере вход J называется единичным установочным входом, а вход К нулевым установочным. В отличие от RS-триггера в JK- триггере допускаются подача входных сигналов J=l и K=l.
Триггеры сохраняют свою память только до тех пор, пока на них подается напряжение питания. Иначе говоря, их память относится к типу оперативной (в отличие от постоянной памяти и перепрограммируемой постоянной памяти, которым отключение питания не мешает сохранять информацию). После выключения питания и его последующего включения триггеры переходят в случайное состояние, то есть их выходные сигналы могут устанавливаться как в уровень логической единицы, так и в уровень логического нуля. Это необходимо учитывать при проектировании схем.
Большим преимуществом триггеров перед другими типами микросхем с памятью является их максимально высокое быстродействие (то есть минимальные времена задержек срабатывания и максимально высокая допустимая рабочая частота). Именно поэтому триггеры иногда называют также сверхоперативной памятью. Однако недостаток триггеров в том, что объем их внутренней памяти очень мал, они могут хранить только отдельные сигналы, биты. Триггер можно рассматривать как одноразрядную ячейку памяти.
Неотъемлемой частью для построениея счётчика служит сводная таблица состояний счётчика (таблица 2.2) и его таблица переходов (таблица 2.1).
Таблица 2.1 Таблица переходов счётчика

В таблице истинности анализируется переключение триггеров из одного состояния в другое последовательно, начиная с первого столбца х1., а зачем сопоставляется с таблицей переходов счётчика, результаты записываются со сводную таблицу внутренних состояний счётчика.
Таблица 2.2 Сводная таблица состояний счётчика
| Х | J1 | K1 | J2 | K2 | J3 | K3 | J4 | K4 | J5 | K5 |
| - | ||||||||||
| - | - | |||||||||
| - | - | - | ||||||||
| - | - | - | - | |||||||
| - | - | - | - | - | ||||||
| - | - | |||||||||
| - | - | - | ||||||||
| - | - | - | - | |||||||
| - | - | - | - | - | ||||||
| - | - | - | - | - |
Для построения счетчика с помощью карт Вейча необходимо далее получить функции логических уравнений. В карте Вейча есть свой порядок заполнения. (таблица 2.3)
Таблица 2.3 Карта Вейча

Метод минимизации функции с помощью карт Вейча обеспечивает простоту получения результата. Он используется при минимизации относительно несложных функций ручным способом.. Карга Вейча представляет собой определенную форму таблицы истинности.
Каждая клетка карты соответствует определенному набору значений. Этот набор значений определяется присвоением значения одного буквам, на пересечении строк и столбцов которых расположена клетка.
Карта Вейча — это таблица, число клеток в которой для ФАЛ n -переменных равно 2 n, каждой из клеток поставлен в соответствие некоторый набор входных переменных, причем рядом расположенным клеткам соответствуют соседние наборы входных переменных (кодов), а в самих клетках записаны значения функции, определенные для этих кодов.
При минимизации ФАЛ используют либо ее нулевые, либо единичные значения. На карте Вейча ФАЛ n -переменных выделяют прямоугольные области, объединяющие выбранные значения функции. Каждая область должна содержать 2 k клеток, где k — целое число. Выделенные области могут пересекаться, т.е. одна или несколько клеток могут включаться в различные области. Каждой из выделенных областей соответствует k -куб исходной ФАЛ, который представляется самостоятельным логическим произведением переменных, значения которых в рамках выделенной области остаются постоянными. Каждое произведение содержит n — k переменных и носит название импликанты. Из полученного множества выбирают минимальное число максимально больших областей, включающих все выбранные значения ФАЛ.
Логически суммируют импликанты, соответствующие выбранным областям.
Карты Вейча заполненные с помощью сводной таблицы состояний счетчика показаны в рисунке 2.2. В диаграмме Вейча объединяяячейки, где расположены логические цифры один мы получаем уравнения для синтеза счетчика.

Рисунок 2.2 - Карты Вейча заполненные с помощью сводной таблицы
состояний счетчика
В результате получаем следующие уравнения:
J1 =  ;
;
K1 = 
 ;
;
J2 = 
 ;
;
K2 = 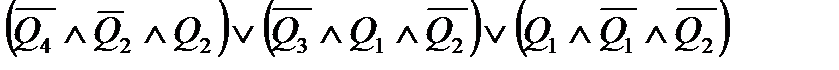 ;
;
J3 =  ;
;
K3 =  ;
;
J4 =  ;
;
K4 =  ;
;
J5 = 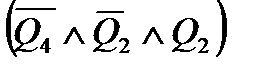 ;
;
K5 = 
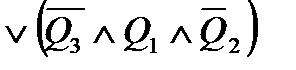 ;
;

Рисунок 2.3 - Микросхема К155ИЕ7 построенного счетчика и его графическое
обозначение
3 КОМБИНАЦИОННЫЕ ЛОГИЧЕСКИЕ
СХЕМЫ (У3,У4 У5).
Комбинационные логические схемы (КЛС) или цифровые устройства комбинационного типа (КЦУ) – это автоматы без памяти. Каждый символ на выходе определяется лишь символами, действующими на входе в данный момент времени и не зависит от того, какие символы были раньше.
В данном разделе нам необходимо выполнить операцию умножения двоичных чисел, для этого используются устройства – конъюнктуры или логические устройства «И».
На рис.3.1 показаны комбинационные схемы, предназначенные для перемножения чисел, заданных в двоичной системе счисления.
При умножении чисел А и В образуются частичные произведения:
А5В1, А4В1, А3В1, А2В1, А1В1 – 1-ое частичное произведение.
А5В2, А4В2, А3В2, А2В2 , А1В2 – 2-ое частичное произведение.
А5В3, А4В3, А3В3, А2В3 , А1В3 – 3-е частичное произведение.
А5В4, А4В4, А3В4, А2В4 , А1В4 – 4-е частичное произведение.
А5В5, А4В5, А3В5, А2В5 , А1В5 А5В1, А4В1, А3В2, А2В2 , А1В2
Для перемножение поразрядно чисел А и В используем микросхему К555ЛИ2.

Рисунок 3.1. Комбинационные логические схемы.
4 ВЫБОР РЕГИСТРА (У6, У7)
Регистр — последовательное или параллельное логическое устройство, используемое для хранения n-разрядных двоичных чисел и выполнения преобразований над ними. Регистр - строится в виде набора триггеров, каждый из которых предназначается для хранения цифр определённого числа. Следовательно, для хранения цифр n-разрядного числа нужен регистр, содержащий n-триггеров. Регистры также используются для выполнения следующих функций: сдвиг хранимого в регистре числа на определённое число разрядов вправо или влево; преобразование числа из параллельной формы в последовательную форму и наоборот.
В зависимости от формы представления числа, вводимого в регистр, регистры делятся на два типа: последовательные и параллельные.
В параллельном регистре все разряды числа поступают на вход одновременно.
В последовательный регистр, ввод числа производится путём передачи цифр отдельных разрядов (обычно начиная с младшего разряда).
Сброс триггеров происходит при подаче логического нуля на вход R.
Регистры сдвига. Регистры с последовательным приемом или выдачей информации называются сдвиговыми регистрами или регистрами сдвига. Регистры сдвига могут выполнять функции хранения и преобразования информации. Они могут быть использованы для построения умножителей и делителей чисел двоичной системы счисления, так как сдвиг двоичного числа влево на один разряд соответствует умножению его на два, а сдвиг вправо - делению на два. Регистры сдвига широко используются для выполнения различных временных преобразований цифровой информации (преобразование параллельного кода в последовательный). Регистры сдвига могут служить также в качестве элементов задержки сигнала, представленного в цифровой форме.
5 ВЫБОР СУММАТОРА (У8, У9)
Далее нам необходимо сложить полученные частичные произведения, эту операцию производят устройство, называемые сумматорами. Сумматор – это цифровое устройство, предназначенное для арифметического сложения двух чисел.
Одноразрядный полный сумматор представляет собой логическую цепь, вырабатывающую сигнал одного разряда суммы S и переноса P при сложении двух двоичных чисел. Полный сумматор имеет на входе два слагаемых и один перенос, на который подается сигнал с выхода переноса соседнего младшего разряда.
Сумматор не обладает памятью, то есть информация на его выходе меняется при изменении входных сигналов. Сумматор работает в соответствии с таблицей состояний.
Многоразрядный сумматор- сумматор паралельного действия содержит одноразрядные сумматоры, число которых равно разрядности суммируемых двоичных слов.При суммировании многоразрядных чисел сумматоры включаются покаскадно, для чего выход P1 предыдущего разряда соединяется со входом P0 последующего.
Вычитание двоичных чисел производится также с помощью сумматора. При этом операцию вычитания заменяют операцией суммирования путем замены кода уменьшаемого числа на дополнительный, а разряд переполнения P не учитывается. Добавление единицы реализуется выдачей сигнала «1» на вход переноса сумматора самого младшего разряда.
Согласно нашему заданию, для операции суммирования нам понадобится три четырехразрядных сумматора.

Рисунок – 4.1 Микросхема К155ИМ3
6.РЕГИСТР, ПРЕОБРАЗУЮЩИЙ
ПАРАЛЛЕЛЬНУЮ ФОРМУ
ДВОИЧНОГО ЧИСЛА В
ПОСЛЕДОВАТЕЛЬНУЮ (У10)
Регистр – последовательное устройство, предназначенное для записи, хранения и сдвига информации, предсавленной в виде многоразрядного двоичного кода. Регистр состоит из триггеров и вспомогательных логических схем. В регистрах выполняется ряд микроопераций. К ним относятся: установка разрядов регистра в нулевое или единичное состояние; прием слова из другого устройства; выдача слов из регистра в прямом или обратном кодах; сдвиг слов в разрядной сетке влево или вправо; преобразование последовательного кода слова в параллельный и обратно. Регистры строятся на D, RS, JK-триггерах.
В этом разделе преобразовываем параллельную форму полученного произведения в последовательную форму для последующего вывода в линию связи. На рисунке 6.1 показана микросхема К555ИР9 – восьмиразрядный сдвигающий регистр с возможностью асинхронной параллельной записи и последовательного считывания. Она имеет вход D0 для подачи информации при последовательной записи, входы D1 – D8 для подачи информации при параллельной записи, два равноправных входа для подачи тактовых импульсов, прямой и инверсный выходы последнего разряда сдвигающего регистра.
Переключение триггеров регистра происходит по спаду импульса отрицательной полярности на любом из входов С при логическом нуле на другом.
Подача логической единицы на любой из этих входов запрещает переключение триггеров при подаче импульсов на другой вход.
Режим работы регистра определяется сигналом на входе L: при логической единицы по спадам импульсов на входе С происходит сдвиг информации, поступающей на вход D0, к выходам В; при логическом нуле на входе L происходит параллельная запись информации со входов D1 – D8 в триггеры регистра.

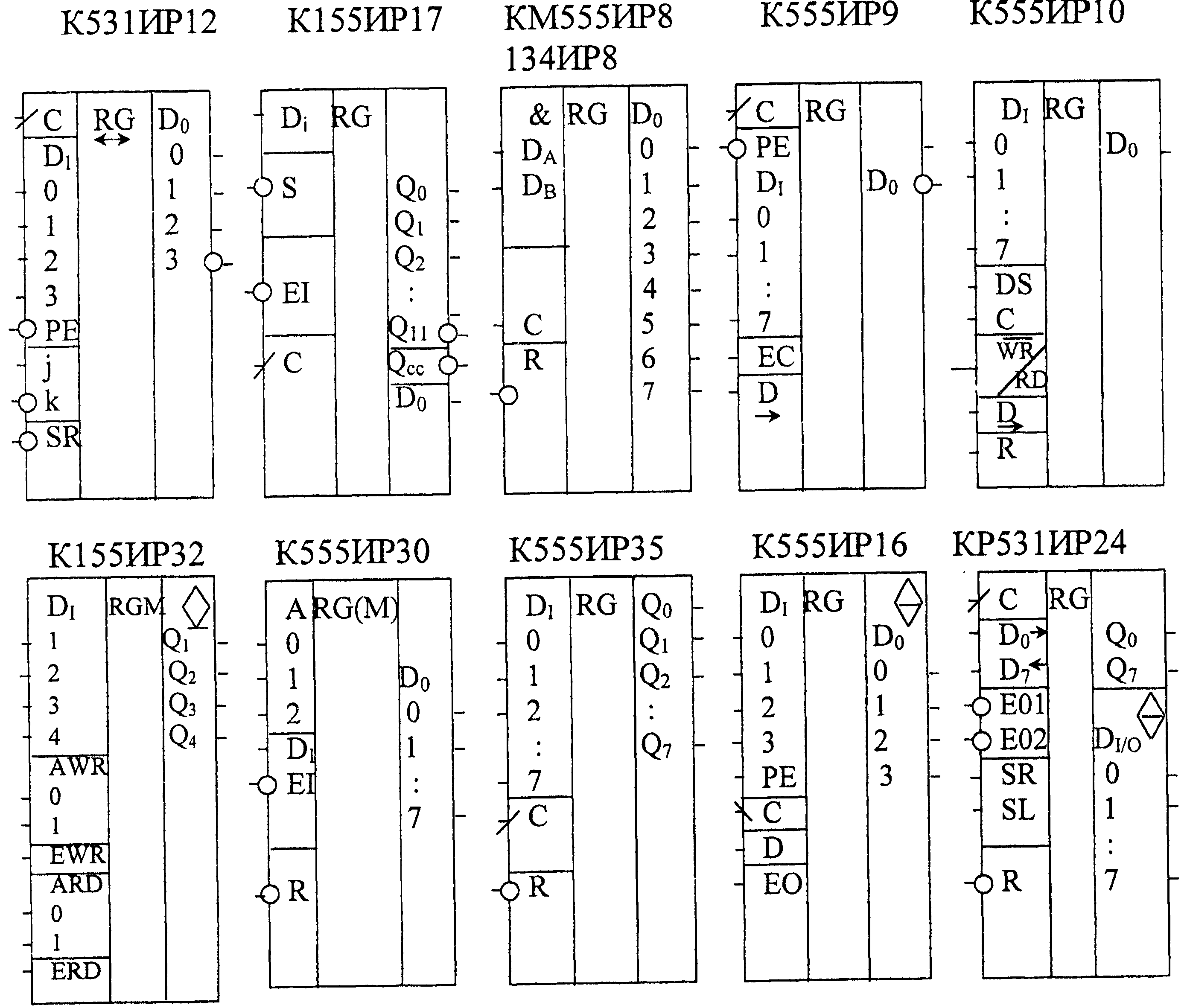
Рисунок 6.1 Параллельно-последовательный сдвигающий регистр К555ИР10
Микросхема К555ИР10 – восьмиразрядный сдвигающий регистр с возможностьюассинхронной параллельной записи и последовательным считыванием. Микросхему К555ИР10 удобно использовать для преобразования параллельного кода в последовательный. Наличие двух ходов для подачи тактовых импульсов позволяет использовать один из них как вход разрешения работы регистра, другой для выполнения сдвига или записи.
7.ПОЛНАЯ ПРИНЦИПИАЛЬНАЯ
ЭЛЕКТРИЧЕСКАЯ СХЕМА
ЦИФРОВОГО УМНОЖИТЕЛЯ
ПОЛОЖИТЕЛЬНЫХ ЧИСЕЛ
На рисунке 8.1 показана полная принципиальная электрическая схема цифрового умножителя положительных чисел.
В разработанной принципиальной схеме цифрового устройства умножителя положительных чисел был предусмотрен ввод четырёхразрядного множимого А и четырёхразрядного множителя В.
В курсовой работе шифратор реализован на микросхемах DD1-DD8. На выходах микросхемы вырабатывается двоичный код числа (5(10) = 1011(2), код шифратора – 2421). С выхода счётчика, который реализован на микросхеме К155ИЕ5, вырабатывается код числа (4(10) = 0100(2)). Далее производится операция умножения схемами КЛС1, КЛС2, КЛС3, выполненные в микросхеме К555ЛИ3.
Каждое частичное произведение, начиная со второго, сдвигается на один разряд в лево – эту операцию выполняет регистр сдвига К155ТМ8 в количестве двух штук. Затем, полученные частичные произведения складываются двухразрядными сумматорами микросхемы К155ИМ2, и полученный результат выдаётся в линию связи, в последовательном виде начиная с младшего разряда.
8 СПЕЦИФИКАЦИЯ
| Позиционные обозначения | Наименование | Количество | Примечание |
| DD1-DD8 | К155ЛЕ1 | 8 шт. | - |
| DD9 | K155ИЕ5 | 1 шт. | Один вход не используется |
| DD10 | К555ЛИ3 | 1 шт. | В качестве обратной связи |
| DD11-DD13 | К555ЛИ3 | 6 шт. | - |
| DD14-DD15 | К155TM8 | 2 шт. | - |
| DD16-DD17 | К155ИM2 | 2 шт. | - |
| DD18 | К555ИP9 | 1 шт. | - |
ЗАКЛЮЧЕНИЕ
В курсовой работе было построено устройство умножения двоичных положительных чисел. В начале был дан код 2421 и числа А и В в базисе ИЛИ. Умножитель предназначен для умножения двоичных чисел A и B, представленных разрядами А1, А2, А3, А4, и В1, В2 В3. На выходе умножителя формируется шестизначное произведение Q, представленное разрядами S1, S2, S3, S4, S5, S6, S7. Было произведено умножение чисел А и В. С помощью шифратора число А был преобразован с десятичной системы счисления в двоичный код. Далее был произведен синтез счетчика. Использовался JK-триггер, так как он является универсальным.
Умножителем называется комбинационное цифровое устройство, формирующее на выходе число Q, равное произведению входных двоичных чисел A и B. Предполагается, что числа A, B и Q представлены в двоичной позиционной системе счисления. Арифметическое перемножение одноразрядных чисел (АiВj) реализуется конъюнктором, поскольку логическое умножение совпадает с арифметическим.
СПИСОК ИСПОЛЬЗУЕМОЙ ЛИТЕРАТУРЫ
1 Бирюков С. А. Применение интегральных микросхем серии ТТЛ. –М.: Патриот, 1992. – 120 с.
2. Қалабеков Б.А. «Цифровые устройства и микропроцессорные системы»
3. Белов А.В «Самоучитель по микропроцессорной технике»
4. Безуглов Д. А., Калиенко И. В. Цифровые устройства и микропроцессоры. Учебник для ВУЗов – Ростов-на-Дону: Еникс, 2006. – 480 с
5. Червоненко И.П., Багутдинов Р.А. Учебное пособие: «Цифровые устройства и микропроцессорные системы» - Караганда.: ИИЦ КПТК., 2008 г.-187 с.






