Ші деңгей
Исықсызықты жүйелердің фазалық суреттерінің ерекшеліктері
Фазалық суреттері сапалы түрде тұрғызу үшін ерекше траекториларды: ерекше нүктелер, шекті циклдер және сепаратриссалар анықтаған жеткілікті.
Түйін, фокус немесе ер тоқым типті ерекше нүкте деп уақыт өткен сайын кескіндеуші нүкте оған жақандайтын (тепе-теңдіктің тұрақты жағдайында) немесе одан кескіндеуші нүкте алыстайтын (тепе-теңдіктің тұрақсыз жағдайында) нүктені атаймыз.
Фазалық траекторияның абсцисса өсіне қисаю бұрышы α келесідей анықталады:
(10-8)
мұнда α – қисаю бұрышы.
Егер 
болса, анықталмағандық пайда болады. Анықталмағандыққа сәйкес нүктелер ерекше нүкте деп аталады. анықталмағандақты 
Лопиталь ережесімен аша отырып (F1 және F2 Тейлор қатарына жіктеп және оларды түзулендіріп), ерекше нүктенің типтерін анықтайды (түйін, фокус, ер тоқым).
Ер тоқымның» өтпелі процесі
Ер тоқымның» фазалық траекториясы
Барлық өтпелі процес түрлері үшін фазалық траектория уақыт өтуіне байланысты бір координаталар бойынша координата басына ұмтылады, ал басқа координаталар бойынша координаталар басынан алшақтайды.
Исықсызықты жүйелердің фазалық кескіндерін құру үшін қандай әдістер қолданады
Гармоникалық түзулендіру әдісі. Егер болымды қисықсызықты жүйелерді түзулендіргенде кіріс сигналы ретінде гармоникалық сигнал қолданылса, онда бұл әдіс гармоникалық түзулендіру әдісі деп аталады.
x(t) = A Sin ωt
Статистикалық түзулендіру әдісі. Егер кіріс сигналы x(t) ретінде кездейсоқ функция қолданылса, онда әдіс стохастикалық немесе статикалық түзулендіру әдісі деп аталады.
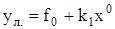
Басқару нысаналарының негізгі динамикалық сипаттамалары
Басқару жүйелерінің динамикалық сипаттамаларының бірі болып өтпелі функция саналады. Түзу сызықты жүйенің жалпы дифференциалдық теңдеуін қарастырайық:
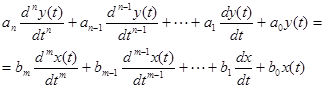(3-1)
Берілген теңдеуді Лаплас бойынша түрлендіріп, нольдік бастапқы шарттарды қабылдай отырып келесіні жазуға болады:
(3-2)
Интегралдаушы түйіннің электрлі моделі
 |
Uвх. С Uвых.
Суперпозиция принципінің негізгі жағдайлары
1) Түзу сызықты жүйелер үшін екі немесе оданда қөп әсерлерге жүйенің реакциясы қосындысы осы әсерлердің әр қайсысына реакция қосындысына тең.
(1-16)
2) Егер кіріс сигналын k есе үлкейтсе немесе кішірейтсе, онда шығу сигналы да сонша есе үлкейеді.
8. Лаплас бойынша түпнұсқалар және көріністер мәлімет таблицасы
| Түпнұсқа | Қөрініс | |
| 1. | 1(t) | 
|
| 2. |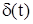 
| |
| 3. | 
| 
|
| 4. | 
| 
|
| 5. | 
| 
|
| 6. | 
кешігу
| 
|
| 7. | 
| 
комплексті жазықтықта жылжу
|
| 8. |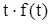 
| 
|
| 9. | 
| 
|
| 10. | 
| 
|
| 11. | T | 
|
| 12. | t2 | 
|
| 13. | Sin ωt | 
|
| 14. | Cos ωt | 
|
| 15. | 
| 
|
| 16. | 
| 
|
Рылымдық схеманы түрлендіруге жүйені есептеу мысалы
Құрылымдық схема берілген:
Кіріс Х X1 1 Y1 Шығыс У
Y3 X3 Y2 X2
3 2
4-4 сурет.
Айнымалыларды X1, Y1, X2, Y2, X3, Y3 белгілеп тиісті түйіндер теңдеулерін жазамыз:
Исықсызықты басқару жүйесінің жылдамдығы бойынша тиімді құрылымдық схемасы
Шектемелі күшейткіш түйін арқылы синусоидальді сигнал өткендегі динамикалық сипаттамасы
Люфт арқылы синусойдальді сигнал өткендегі динамикалық сипаттама
