Помехоустойчивое кодирование в системах мобильной радиосвязи

Особенностью радиолиний по сравнению с кабельными яв­ляется повышенный уровень помех и искажений передаваемого сигнала (см. гл. 3). При цифровой передаче данных результатом этого являются ошибочные решения приемной стороны относи­тельно значения переданного символа. Для обнаружения и ис­правления возникающих ошибок применяется помехоустойчивое кодирование, суть которого сводится к введению избыточности в передаваемое сообщение. В двоичном случае каждому сооб­щению из к информационных бит сопоставляется кодовое слово длиной n > к бит (символов) согласно некоторому правилу кодирования.

Важнейшей характеристикой кода является скорость передачи (7.1)

Так как для безызбыточного кода R_k =1, то (7.1) показыва­ет, за счет какого снижения скорости передачи достигается тре­буемая достоверность приема. Поэтому основная задача по­строения хорошего кода состоит в минимизации избыточности, гарантирующей необходимое качество передачи.

Возможны случаи, когда биты передаваемого сообщения неравноценны по степени влияния их искажений на восстанавли­ваемое сообщение. При этом разумно раздельно закодировать группы информационных битов, отводя большую избыточность группам с большей ответственностью. Так, для речевого кодека (см. гл. 9) выделяются и защищаются кодом старшие разряды коэффициентов а„ периодов основного тона, коэффициентов усиления (всего 30 из 137 бит). Для защиты остальных бит вво­дится значительно меньшее число избыточных символов.

Помехоустойчивое кодирование иначе называется каналь­ным кодированием, поскольку предназначается для нейтрализа­ции канальных помех. В системах мобильной связи канальное кодирование выполняется в несколько этапов, как показано на Рис. 7.1. В зависимости от важности логических каналов для них

предусматриваются разные наборы указанных процедур, разные типы кодов и их параметры. Обычно полный набор процедур со­держат каналы трафика и синхронизации.

В блоковых (блочных) кодах Kсимволам источника сопос­тавляется кодовое слово из nсимволов. В сверточных кодируе­мая последовательность не разбивается на блоки. Кроме того, выделяют систематические (разделимые) коды, в словах которых можно указать позиции с символами сообщения, и несистемати­ческие, кодовые слова которых не обладают этим свойством. На­помним кратко некоторые положения теории помехоустойчивого кодирования, отсылая читателя за подробностями к популярным монографиям [43-46].

Блоковые коды

Бинарные блоковые коды чаще всего рассматриваются в предположении, что источник безызбыточный, формирующий k-битовые блоки А = (а₁, а₂,..., а_к) двоичных символов а_j =0,1

с равной вероятностью 1/ М, где М = 2^к, а для передачи исполь­зуется двоичный симметричный канал (ДСК) без памяти, наблю­дением на выходе которого является вектор

 

кодовый вектор (кодовое слово), а вектор ошибок с независи­мыми компонентами. При этом элементы y_j,s_j,e_j упомянутых векторов принимают двоичные значения 0 и 1, а символ "+" всюду в этом разделе обозначает поэлементное суммирование по мо­дулю два. В ДСК вероятность появления конкретного вектора ошибки Е убывает при увеличении кратности ошибки t (т.е. числа 1 в векторе Е, или, что равносильно, числа искаженных сим­волов в переданном кодовом векторе). Поэтому оптимальной (максимально правдоподобной) стратегией декодирования ока­зывается правило минимального расстояния Хэмминга, согласно которому принятый вектор Y должен декодироваться в ближай­ший к нему, по Хэммингу, кодовый вектор С. Напомним, что в двоичном случае расстояние Хэмминга между Y и С есть про­сто число единиц среди элементов вектора Y + С.

Под термином код понимается множество из М кодовых слов. Отметим, что для произвольного кода с большим числом слов реализация оптимального правила декодирования может оказаться чрезвычайно затратной в аппаратно-программном от­ношении. Из-за существования довольно простых алгоритмов декодирования наибольшее применение находят линейные коды, являющиеся линейными подпространствами. В системах мо­бильной связи, в частности, нашли применение линейные коды Хэмминга, БЧХ, Голея, Рида-Маллера, Рида-Соломона (PC).

Параметры линейного кода n(длина или размерность про­странства, в котором задан код) и K (число информационных бит или размерность кода) - определяют его избыточность п-к (число проверочных символов), скорость (7.1) и входят в его тра­диционное обозначение (n, к). В слове систематического кода

длины n, как правило, первые к символов являются информа­ционными, в то время как оставшиеся п-к позиций принадле­жат избыточным символам, создаваемым кодером. Корректи­рующая способность оценивается с помощью кодового расстоя­ния d₀ - минимального расстояния Хэмминга между всевозмож­ными парами кодовых слов. Чем больше d₀, тем выше помехо­устойчивость кода, а именно максимальное число (кратность) символьных ошибок, гарантированно обнаруживаемых кодом

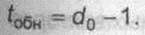
Если же код используется для исправления ошибок, то это с гарантией выполнимо, если их кратность не превосходит

где (•) - целая часть числа. В случае, кода код

должен исправлять какое-то количество ошибок t_испр и сверх это-
обнаруживать t_обн >t_испр ошибок, его расстояние должно быть
не меньшим

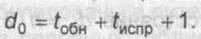
Для задания кода и, следовательно, для вычисления кон­трольных символов по известным информационным можно использовать один из возможных способов задания подпространст­ва размерности к в пространстве размерности п. Напомним, что задание пространства предполагает и задание поля, откуда бе­рутся коэффициенты разложения вектора по базису (координаты вектора). Вышеперечисленные коды, кроме кода Рида-Соломона, заданы над двоичным полем, а последний - над расширением двоичного, имеющим 2^т элементов, где т - натуральное число.

Каждый проверочный бит b_j, есть линейная комбинация не­которых вполне определенных информационных, например, bj =a₁+a₃+a₆. Благодаря свойствам сложения по модулю 2 по­следовательность а₁, а₃, а₆, b_j, содержит четное число символов 1.

Поэтому проверочные символы часто называют битами контроля четности или просто битами четности.

Классические способы задания линейного кода связаны с порождающей матрицей G, строками которой являются K ли­нейно независимых кодовых слов (базис кода)

и проверочной матрицей, Н, обладающей свойством(7.2)

где верхний индекс Т означает транспонирование; 0 - нулевой вектор. Поясним на следующем примере смысл порождающей матрицы.

Пример 7.1. Порождающая матрица кода Рида-Маллера (8,4) первого порядка имеет вид

Кодовое слово есть линейная комбинация базисных векторов

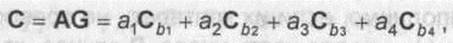
где А = (а₁, а₂, а_3, а₄) - информационные биты. Так, если А = 0110, то С = 00111100, при А = 1110 - С = 11000011. Коды Рида-Маллера первого порядка существуют для любых длин п = 2^k-1 и имеют минимальное расстояние d₀ = n/2. Отметим связь кодов Рида-Маллера с широко распростра­ненными в цифровой связи функциями Уолша.

При замене двоичных символов 0 и 1 на +1 и -1 соответственно операция сло­жения по модулю 2 перейдет в умножение действительных чисел +1 и -1. При таком отображении базисные векторы кода дадут функции Радемахера (меандры, период каждого из которых равен половине периода предыдущего), а остальные кодовые слова -прямые и противоположные функции Уолша, равные различным произведениям функций Радемахера (так называемые биортого-нальные сигналы). Функции Уолша (ортогональные коды) приме­няются в системе стандарта IS-95, а также в системах третьего поколения (см. гл. 11, 12).

Проиллюстрируем теперь роль проверочной матрицы в по­строении линейного кода.

Пример 7.2. Пусть проверочная матрица кода Хэмминга (7,4) с расстоянием d₀ = 3, столбцами которой являются все 7 ненулевых 3-разрядных двоичных векторов, имеет вид

Если кодовое слово

подставить в (7.2) и выполнить матричное умножение, то получим соотноше­ния для вычисления контрольных бит по информационным:

В системах связи весьма распространены циклические ко­ды, составляющие подкласс линейных, для которых разработаны эффективные процедуры декодирования. Они задаются с помо­щью порождающего многочлена g (х) степени n- K. При этом ка­ждому кодовому слову формально сопоставляется многочлен с коэффициентами, равными элементам кодового вектора. Так, кодовому слову С = (с₁, с₂,.., с_n) соответствует многочлен

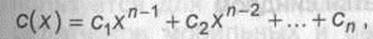
делящийся без остатка на порож­дающий g(х), т.е. c(x) = f(x)g(x), где f(x) - произвольный много­член. Порождающие многочлены хороших циклических кодов, в том числе БЧХ и PC (являющихся подклассом недвоичных ко­дов БЧХ), табулированы в литературе [43].

Когда в подобных таблицах не находится кода с подходя­щими значениями параметров n, к, можно поискать его среди укороченных циклических кодов. Для этого из слов циклического кода с К^’ > к информационными символами отбираются только те, у которых первые к' - к символов нулевые. Эти первые символы затем отбрасываются (не передаются по каналу), поскольку де­кодер знает, что они нулевые. Полученный (n-k' + k,k) линей­ный код, не являясь, строго говоря, циклическим, тем не менее, может быть декодирован теми же способами, что и исходный. Минимальное расстояние укороченного циклического кода, разу­меется, не меньше расстояния исходного кода, чем и объясняет­ся широкое использование приема укорочения на практике.

Слова циклического кода с любым заданным порождающим многочленом можно переупорядочить, преобразовав код в систе­матический. Для этого информационная последовательность А (многочлен а(х)) сдвигается влево на n-к позиций: a_1, a₂,...a_k, 0,0,...,0_, что соответствует умножению а(х) на х^n-k. Далее вычисляется остаток Ь(х) от деления полученного много­члена (7.3)

Степень полученного остатка Ь(х) не превышает n - k, т.е. степени порождающего многочлена д(х). Вычитание (равносиль­ное для кодов над полями характеристики 2 прибавлению) остат­ка из многочлена а(х)х^n-k дает требуемый кодовый многочлен

Обсудим кратко процедуры декодирования линейных и циклических кодов.

Для обнаружения ошибок декодер проверяет принадлеж­ность принятой последовательности Y данному коду (подпро­странству): если Y является кодовым словом, то принимается решение об отсутствии ошибок, в противном случае фиксируется наличие ошибки. Для этого вычисляется синдром (7.4)

который с учетом (7.2) не зависит от кодового слова и определя­ется только вектором ошибки Е.

Если S = 0, то Y является одним из М кодовых слов и, сле­довательно, максимально правдоподобная оценка вектора ошиб­ки Ё = 0. Решение об отсутствии ошибок будет правильным, если в действительности Е = 0. Но согласно (7.2) синдром S = 0 и в случаях, когда Е совпадает с любым ненулевым кодовым сло­вом. Такие ошибки не будут обнаружены. Их общее количество составляет 2^k -1. Для кода примера 7.2, в частности, трехкрат­ные ошибки Е = 1110000 и Е = 0011010 дают нулевой синдром и не обнаруживаются.

Если S ≠0, то принимается всегда правильное реше­ние Ё ≠0.

Для обнаружения ошибок рекомендуется использовать про­токол контроля циклическим избыточным кодом - ЦИК (в зару­бежных источниках CRC - cyclic redundancy code). Для информа­ционной последовательности А произвольной длины K по (7.3) вычисляется остаток Ь(х), который передается вместе с А. На

приемной стороне по А' снова вычисляется остаток Ь(х), кото­рый сравнивается с принятым Ь'(х), т.е. фактически определяет­ся синдром. При их равенстве выносится решение об отсутствии ошибок, в противном случае - о наличии. Доля пропущенных

ошибок –

зависит только от степени т многочлена д(х). Например, в транкинговых системах TETRA ис­пользуются многочлены с т = 7 и т = 16.

В случае обнаружения ошибки действия приемной стороны могут быть различными. При передаче команд управления воз­можен запрос по обратному каналу о повторении искаженного блока. В случае передачи речевых сообщений сопутствующая этому задержка может быть недопустимо велика, поэтому чаще испорченный блок просто выбрасывается и заменяется преды­дущими. В пейджинговых системах искаженный символ отмеча­ется на экране индикатора скобками в надежде, что абонент сам по смыслу догадается о его значении.

В системах мобильной связи обнаружение ошибок ис­пользуется для регулировки уровней излучаемой мощности пе­редатчиков мобильных и базовых станций. В приемниках этих станций в режиме обмена сообщениями непрерывно подсчитывается частота появления ошибочных бит. Если на БС частота ошибок в сообщениях МС превышает заданный порог, то данной МС посылается команда на увеличение излучаемой мощности. Мобильная станция тоже измеряет и передает на БС частоту об­наруженных ошибок в принятых битах. В зависимости от частоты ошибок БС регулирует уровень мощности сигнала, адресованного этой МС (см. §6.1).

Преимущество линейных кодов, как уже сказано, состоит в упрощении для них максимально-правдоподобной процедуры декодирования. Для исправления ошибок и, следовательно, для оценки переданного кодового слова пространство принятых по­следовательностей Y разбивается на 2^n-k смежных классов, ка­ждый из которых характеризуется тем, что разности любых вхо­дящих в него векторов являются кодовыми словами. Для каждого класса заранее определяется максимально правдоподобный век­тор ошибок Е₁ (лидер), сдвигающий любое кодовое слово в дан­ный смежный класс. Задача декодера состоит в определении но­мера смежного класса (синдрома), в который попадает принятый вектор Y. По синдрому определяется (считывается из памяти де­кодера) лидер Е₁. Каждому ненулевому синдрому может быть сопоставлен некоторый лидер. В результате максимальное число исправляемых ошибок равно 2^n-k -1. Схематично процесс деко­дирования показан на рис. 7.2.

Если реальная ошибка, имевшая место в канале, совпадает с лидером Е = Е₁, она будет исправлена.

При больших n-k наиболее сложной операцией является сопоставление синдрому вектора Е,.

Как следует из (7.4), для однократных ошибок синдром ра­вен транспонированному столбцу проверочной матрицы с номе­ром, равным номеру искаженного бита. Поэтому для исправления всех однократных ошибок требуется, чтобы столбцы проверочной матрицы были ненулевыми и не повторялись. Матрица из приме­ра 7.2 обладает этим свойством, и любая из 7 возможных одно­кратных ошибок данным кодом исправляется. Действительно, если Е = 0010000, то S = 101, которому в декодере заранее со­поставлен лидер Е, = 0010000, совпадающий с фактическим век­тором ошибки.

Однако указанный синдром может появиться и при возник­новении двукратной ошибки, например, при Е = 1100000 или Е = 0001010. Декодер, действуя по схеме на рис. 7.4, по-прежнему добавит к принятой последовательности Е, = 0010000, так что в результате ошибка не только не исправится, но ее крат­ность возрастет до 3. Для исправления ошибок большой кратно­сти требуется увеличивать кодовое расстояние.

Аппаратная сложность синдромного декодера экспоненци­ально растет с числом проверочных символов и потому его реа­лизация для длинных кодов, исправляющих многократные ошиб­ки, может оказаться проблематичной.

Примерами блоковых кодов с высокой исправляющей спо­собностью, нашедших применение в мобильной связи, могут слу­жить 256-ричные (15,3) PC коды, являющиеся основой вторичного канала синхронизации в 3G стандарте UMTS (см. § 12.2.11).

Для декодирования кодов БЧХ, один из недвоичных под­классов которых составляют PC коды, разработаны квазиопти­мальные алгебраические алгоритмы, которые, уступая алгоритму максимального правдоподобия, тем не менее, обеспечивают ис­правление ошибок в пределах, гарантируемых кодовым расстоя­нием. В основе их лежит не векторное описание ошибок, которое, как показывают рассмотренные примеры, обладает избыточно­стью за счет многих нулей, а просто указание номеров позиций, в которых произошло искажение символа. Так, для задания в примере 7.2 двукратных ошибок Е = 1100000 или Е = 0001010 проще сказать, что в первом случае искажены биты на 1-й и 2-й позициях, а во втором - на 4-й и 6-й.

В алгебраических алгоритмах позициям кодовых символов сопоставляются степени примитивного элемента а расширенно­го конечного поля GF(q), где q = 2^т = n + 1 (натуральное т на­зывается степенью расширения поля). Для примера 7.2 последо­вательность номеров позиций отображается в степени а как

где а - примитивный элемент поля GF(2³). Тогда вышеуказанные двукратные ошибки описываются

так: искажены биты на позициях

Степени а, отве­чающие позициям, содержащим ошибки, называются локатора­ми ошибок.

Рис. 7.2. Схема синдромного декодирования линейного кода

Чтобы компактно описать наборы β₁, β₂,…, β_t локаторов, вво­дят так называемый многочлен локаторов a{z), корнями которого являются элементы, обратные по умножению этим номерам,

Таким образом, первая задача декодера БЧХ и PC состоит в нахождении многочлена локаторов a(z), т.е. его коэффициен­тов при степенях z. Упрощенная схема декодирования кодов БЧХ включает следующие операции.

Полученная из канала последовательность Y делится на полиномы, входящие в разложение порождающего многочлена кода. Остатки от деления связаны с многочленом локаторов клю­чевым уравнением. Решение ключевого уравнения дает оценку многочлена a(z). Поиск корней этого многочлена и инвертирова­ние принятых бит на позициях, соответствующих найденным кор­ням, завершают алгоритм декодирования.

В словах кодов PC, заданных над полем GF(2^m), каждый символ представляет собой т - разрядный двоичный вектор. По­этому для исправления ошибки недостаточно указать номер ис­каженного символа. Требуется еще определить значение искаже­ния, т.е. т - разрядный компонент вектора ошибки. Последний вычисляется по многочлену локаторов и многочлену значений, полученных при решении ключевого уравнения.

Сверточные коды

Сверточные коды относятся к непрерывным рекуррентным ко­дам. Кодовое слово является сверткой отклика линейной системы (кодера) на входную информационную последовательность. Поэтому сверточные коды являются линейными, для которых сумма любых кодовых слов также является кодовой последовательностью.

Ограничимся ниже рассмотрением лишь наиболее харак­терных (базовых, или материнских) для мобильной связи свер­точных кодов со скоростями вида R_k =1/n₀, где п₀ - некоторое натуральное число. Последовательность символов такого сверхточного кода состоит из элементарных блоков длиной п₀, причем п₀ символов текущего блока (занимающие реальное время, от­вечающее одному информационному биту) являются линейной комбинацией текущего информационного бита и m предшест­вующих. Значение m определяет память кода, а параметр m + 1 называется длиной кодового ограничения. Если один (например, первый) из п₀ символов текущего блока повторяет текущий ин­формационный бит, код называется систематическим.

Способы задания сверточных кодов во многом совпадают с используемыми для линейных блоковых. Одним из основных является описание сверточного кода набором п₀ порождающих многочленов. Каждый многочлен устанавливает закон формиро­вания одного из n₀ символов в группе и имеет степень, не пре­вышающую m. Ненулевые коэффициенты порождающего поли­нома прямо указывают, какие из информационных символов (включая текущий и т предыдущих) входят в линейную комби­нацию, дающую данный символ кода (см. пример 7.3). Порож­дающие многочлены хороших сверточных кодов найдены пере­бором и табулированы [44].

Весьма важным с точки зрения понимания алгоритмов ко­дирования и декодирования инструментом описания сверточных кодов является кодовая решетка, смысл которой должен быть ясен из следующего примера.

Пример 7.3 (см. [44]). Пусть несистематический сверточный код со скоростью R_k=1/2 и кодовым ограничением m + 1 = 3 за­дается порождающими многочленами

Это означает, что первый из двух символов каждого двухсимвольного блока является линейной комбинацией (суммой по мо­дулю 2) текущего и двух предшествующих информационных би­тов, тогда как второй получается сложением по модулю 2 текуще­го информационного бита с тем, который поступил от источника Двумя тактами раньше.

Схема кодера приведена на рис. 7.3. Заметим, что при од­ном из многочленов, равном единице, получился бы системати­ческий сверточный код.

 

Кодовая решетка этого кода показана на рис. 7.4. При ее составлении учтено, что кодер содержит память в виде двухраз­рядного сдвигающего регистра. Каждому из четырех возможных состояний этого регистра отвечает один из четырех узлов решет­ки. Поэтому левый символ в обозначении узла равен последнему информационному биту, уже записанному в регистр. При записи в регистр очередного информационного символа регистр меняет состояние на одно из двух соседних. Этот переход обозначен ребрами решетки. Порядок узлов выбран таким, что при нулевом текущем информационном символе (а,- = 0) переход в следую­щее состояние соответствует верхнему ребру, а при а, = 1 - ниж­нему. Маркировка ребер воспроизводит а?₀-6лок, посылаемый в канал. Каждой информационной последовательности соответ­ствует определенный путь на кодовой решетке и кодовая после­довательность, считываемая как метки, маркирующие последова­тельные ребра пути. К примеру, входным информационным би­там 01100 отвечает кодовое слово 00 11 01 01 11, которому соот­ветствует на рис. 7.4 путь, отмеченный жирной линией.

 

 

 

Известен ряд алгоритмов декодирования сверточных кодов. В практических системах и, в частности в мобильной связи, как правило, используется алгоритм Витерби, отличающийся про­стотой реализации при умеренных длинах кодового ограничения.

Алгоритм Витерби реализует оптимальное (максимально правдоподобное) декодирование как рекуррентный поиск на ко­довой решетке пути, ближайшего к принимаемой последователь­ности. На каждой итерации алгоритма Витерби сопоставляются два пути, ведущих в данное состояние (узел решетки). Ближай­ший из них к принятой последовательности сохраняется для дальнейшего анализа как выживший, тогда как другой отбрасы­вается. Таким образом, если игнорировать случаи, когда оба конкурирующих пути равноудалены от принятой последователь­ности (о действиях в подобной ситуации см. ниже), число выжив­ших путей, сохраняемых в памяти, равно числу узлов 2^т. Основ­ные операции алгоритма поясним для кода из примера 7.3.

Пусть передается нулевое кодовое слово, а в канале про­изошла трехкратная ошибка, так что принятая последователь­ность имеет вид 10 10 00 00 10 00... 00.... Результаты поиска ближайшего пути после приема 14 элементарных блоков показа­ны на рис. 7.5. Промежуточные этапы работы декодера при сде­ланных предположениях подробно рассмотрены в [44].

На правой части рисунка видны четыре пути, ведущие в каж­дый узел решетки. Рядом проставлены метрики (хэмминговы рас­стояния этих путей от принятой последовательности на отрезке из 14 блоков). Метрика верхнего пути значительно меньше метрик нижних. Поэтому можно предположить, что верхний путь наиболее вероятен. Однако декодер Витерби, не зная следующих фрагмен­тов принимаемой последовательности, вынужден запомнить все четыре пути на время приема L элементарных блоков. Число L на­зывается шириной окна декодирования. Для уменьшения ошибки декодирования величину L следует выбирать достаточно большой, многократно превышающей длину кодового ограничения, что есте­ственно усложняет декодер. В данном случае L = 15.

 

Отметим, что тактика выбора и последующего анализа только одного пути с наименьшим расстоянием составляет сущ­ность более экономного последовательного декодирования.

На средней части рис. 7.5 видно, что все пути имеют общий отрезок (сливаются от 5-го до 12-го шага) и, следовательно, при­ем новых блоков не может повлиять на конфигурацию этого уча­стка наиболее правдоподобного пути. Поэтому декодер уже мо­жет принимать решение о значении информационных символов, соответствующих этим элементарным блокам.

Левая часть рисунка демонстрирует возможную ситуацию неисправляемой ошибки. Существует два пути с одинаковыми метриками. Декодер может разрешить эту неопределенность двумя способами: отметить этот участок как недостоверный или принять одно из двух конкурирующих решений (информационная последовательность равна 00000... или 10100...). Очевидно, что расширение окна декодирования не позволяет исправить такую ошибку. Ее исправление возможно при использовании кода с большей корректирующей способностью.

Поступление из канала нового элементарного блока вызы­вает сдвиг картинки в окне декодирования влево. В результате левое ребро пути исчезает, а справа появляется новый столбец решетки, к узлам которого должны быть продолжены сохранен­ные пути от узлов предыдущего столбца. Для этого выполняются следующие операции.

1. Для каждого узла нового столбца вычисляются расстоя­ния между принятым блоком и маркировкой ребер, ведущих в данный узел.

2. Полученные метрики ребер суммируются с расстоянием путей, которые они продолжают.

3. Из двух возможных путей оставляется путь с меньшей метрикой, а другой отбрасывается, так как следующие поступаю­щие блоки не могут изменить соотношения расстояний этих пу­тей. В случае равенства расстояний или случайно выбирается один путь, или сохраняются оба.

В результате этих операций к каждому узлу нового столбца вновь ведет один путь. Например, пусть новый блок из канала равен 00. Рассмотрим продолжение пути к нижнему узлу решетки, в который можно попасть из состояния кодера 10 по ребру 01 или из состояния 11 по ребру 10 (см. рис. 7.4). В обоих случаях рас­стояние этих ребер от принятого блока 00 равно 1. Однако сум­марное расстояние пути, продолженного из состояния 10, равно б, а пути из состояния 11 равно 7. Поэтому второй путь будет от­брошен вместе с ребром 01, которое входило в нижний узел на предыдущем шаге декодирования (см. рис. 7.5).

Оценка информационного символа производится по край­нему левому ребру пути в окне декодирования. Согласно правилу построения кодовой решетки принимается, что информационный символ равен 0, если это ребро верхнее, и 1, если ребро нижнее.

Рассмотренный пример поясняет работу декодера в пред­положении, что выходной сигнал демодулятора квантуется на 2 уровня (так называемое жесткое декодирование). Большее число уровней квантования приводит к мягкому декодированию. Установлено, что 8 уровней квантования гарантируют практиче­ски потенциальную достоверность декодирования [45].

Чтобы в этом случае использовать алгоритм Витерби, тре­буется вместо расстояния Хэмминга ввести новое расстояние, точнее учитывающее различие между принятой последователь­ностью (выходным многоуровневым сигналом демодулятора) Y и ожидаемым двоичным кодовым словом С. Например, можно использовать евклидово расстояние или расстояние (7.5)

где

переходная вероятность канала, т.е. условная вероятность появления на выходе демодулятора отсчета у_j - при передаче символа с_j.

Для удобства вычислений (7.5) на практике заменяется на

где m_j - целые положительные числа, количество которых равно числу уровней квантования, причем m_j =0, когда между у_j и с_j -наблюдается наибольшее соответствие [45].

На рис. 7.6 приведен размеченный граф канала при 4 уров­нях квантования, которым приписаны числа m_j равные 0, 1,2, 3.

Граф позволяет определить меру расходимости между Ребрами пути на кодовой решетке и принятыми символами. Если, например, на выходе демодулятора у_j=2, а маркировка ребра проверяемого пути имеет с, =0, то мера расходимости равна 2.

При у_j=2 и наличии на ребре метки с_j =1 расходимость т_j=1. Эти числа суммируются в пределах кадра n₀ и добавляются к ме­ре расходимости продолжаемого пути. Дальнейшие операции ал­горитма Витерби при мягком декодировании совпадают с опера­циями жесткого декодирования. Выигрыш мягкого декодирования составляет около 2 дБ. Так как сложность вычислений при этом возрастает незначительно, то мягкое декодирование широко ис­пользуется в современных системах мобильной связи.

Турбо-коды, предложенные сравнительно недавно [37], яв­ляются результатом совместного использования идей сверточного кодирования с мягким решением и перемежения символов, рассматриваемого в § 7.3. Блок А из k информационных бит че­рез перемежители поступает на N элементарных систематиче­ских сверточных кодеров. Они могут быть различными и иметь разные скорости. Структурная схема кодера при N = 2 показана на рис. 7.7.

На выходах элементарных кодеров 1 и 2 формируются две последовательности проверочных бит В₁ и В₂, что дает скорость, равную 1/3. В общем случае, если кодеры одинаковы, скорость кода равна R_K = 1/(N + 1).

Декодирование турбо-кода выполняется элементарными декодерами с мягким решением с учетом перемежения символов, выполненного на передающей стороно. Структурная схема турбо-декодера для А/ = 2 показана на рис. 1. 8.

Перемежители (П), идентичные перемежителю кодера, со­гласовывают порядок поступления бит А и оценок этих бит, выра­батываемых декодером 1. Деперемежители (ДП) восстанавлива­ют порядок поступления оценок с выхода декодера 2 для первого декодера. Таким образом, при оценке символа учитываются не только принятые биты, но и мягкие решения, вынесенные каждым элементарным декодером. Турбо-кодом являются единственными из известных, позволяющими работать со скоростями, близкими к пропускной способности канала с ограниченной полосой. Со­гласно документам 3GPP (см. гл. 12)" их планируется использо­вать в мобильных системах третьего поколения.

 

Перемежение символов

Большинство из известных хороших кодов ориентировано на модель случайных независимых ошибок, т.е. канал без памя­ти. Для систем же мобильной связи (в числе многих других) ха­рактерны глубокие замирания радиосигнала (см. гл. 3), озна­чающие корреляцию ошибок, в результате которой последние группируются в пакеты. При этом появление на выходе демоду­лятора L > 1 неверных символов может стать более вероятным, чем появление только одного. В принципе существуют специаль­ные коды, корректирующие пакетные ошибки большей кратности, чем кратность контролируемых случайных ошибок [43], однако на практике чаще прибегают к более испытанному средству, како­вым является перемежение, приспосабливающее традиционные коды к каналам с памятью.

Поясним смысл перемежения для блоковых кодов. Пусть биты каждого кодового слова посылаются в канал не друг за дру­гом, а через интервалы, превышающие длину пакета ошибок Е. В промежутки между битами одного слова вставляются биты дру­гих кодовых слов, как это показано на рис. 7.9. Тогда пакет Е, по-прежнему искажая в канале L подряд битов, тем не менее, исказит всего по одному биту разных L кодовых слов. На приемной стороне производится обратная перестановка (деперемежение). Биты каждого кодового слова собираются вместе и декодируются алгоритмами, разработанными для независимых ошибок. Поэтому говорят, что перемежение трансформирует ка­нал с пакетами ошибок в канал с независимыми ошибками.

Предложено много алгоритмов перемежения, в частности по периодическим и псевдослучайным законам, блочные и сверточные [45].

При блочном перемежении входные биты делятся на блоки по к бит, которые последовательно записываются в J строк таблицы, приведенной на рис. 7.10. Количество столбцов в ней n≥k/J.

 

Считывание по столбцам дает выходную последователь­ность, в которой соседние входные биты разнесены на J позиций (см. рис. 7.9). Деперемежение заключается в выполнении обрат­ных действий: записи принятой последовательности Y в столбцы такой же таблицы и считывания по строкам. Для борьбы с длин­ными пакетами ошибок желательно увеличивать размеры табли­цы. Однако это приводит к увеличению задержки в отправке и декодировании сообщения.

Алгоритм перемежения может быть задан аналитически. Так, соответствие выходных бит перемежителя входным С_ВЫХ(j)=C_ВХ(j) можно определить по формуле [4]

j = 1 + ((J_i)mod k), / = 1,2,3,...,k.

В стандарте TETRA, например, J = 103, к = 412.

Следует отметить, что если некоторые параметры правил перемежения сделать секретными, например, считывать столбцы в таблице рис. 7.10 в порядке, определяемом секретным ключом, то получится шифрование данных методом перестановки (см. §8.1).